编译原理 2：语言及其文法

编译原理 2：语言及其文法

编译器能够阅读高级语言的代码，而后输出低级语言的代码。因此，为了能够让编译器自动的分析语言，我们就需要将语言学相关的知识提供给计算机。因此，我们首先需要从数学上形式化的定义语言，而后再在计算机中表示语言。

对语言进行数学上形式化的定义，这就是本章的任务。

1 基本概念

我们先定义语言中的的一些基本概念

A. 字母表 Alphabet

我们将一个有穷符号集合 $\Sigma$ 称为字母表（Alphabet）

符号可以是：

• 字母、数字、标点符号、……

B. 字母表上的运算

既然字母表是一个集合，我们就可以利用集合的运算定义字母表上的运算。

1. 乘积 （Product）

定义字母表$\Sigma_1$和$\Sigma_2$的乘积为

$$\Sigma_1\Sigma_2 = \{ab | a \in \Sigma_1, b \in \Sigma_2\}$$

注意：

• 字母表的乘积的结果是一个集合
• 字母表的乘积得到的集合中每一个元素都是两个字母表中符号的拼接，长度会增加

例如：

2. $n$次幂（Power）

定义字母表$\Sigma$的$n$次幂为：

$$\left \{ \begin{aligned} \Sigma^0 &= \{\varepsilon\} \\ \Sigma^n &= \Sigma^{n-1}\Sigma, &n\geq 1 \end{aligned} \right .$$

注意：

• 字母表的$n$次幂得到的就是长度为$n$的符号串构成的集合
• 字母表的$0$次幂得到的是长度位0的串组成的集合，对于长度位$0$的串，称为空串，用符号$\varepsilon$表示

例如：

3. 正闭包（Positive Closure）

定义字母表$\Sigma$的正闭包为

$$\Sigma^+=\Sigma\cup\Sigma^2\cup\Sigma^3\cup\cdots$$

用符号$\Sigma^+$表示。

注意：

• 字母表的正闭包实际上就是由长度为正数的串构成的集合

例如：

4. 克林闭包（Kleene Closure）

定义字母表$\Sigma$的克林闭包为

$$\Sigma^*= \Sigma^0 \cup \Sigma^+ = \Sigma^0 \cup \Sigma\cup\Sigma^2\cup\Sigma^3\cup\cdots$$

用符号$\Sigma^*$表示。

注意：

• 字母表的克林闭包实际上就是字母表的正闭包再加上一个空串组成的
• 字母表的克林闭包实际上就是任意符号串（长度可以为零）构成的集合

例如：

C. 串 String

定义：设是$\Sigma$一个字母表，$\forall s\in\Sigma^*$，则称$s$为是$\Sigma$上的一个串。

注意：

• 串实际上就是字母表中符号的一个有穷序列

串$s$的长度记为$|s|$，是指$s$中符号的个数。

例如：

空串是指长度为$0$的串，用符号$\varepsilon$表示。则有：

D. 串上的运算

类似于我们可以对字母表定义运算，我们也可以针对串定义串的运算

1. 连接（Concatenation）

如果$x$和$y$是串，那么$x$和$y$的连接定义为将串$y$附加到串$x$后面而形成的串，记作$xy$。

例如：

此外，空串是连接运算的单位元（identity），即，对于任何串$s$都有：

$$\varepsilon s = s\varepsilon = s$$

此外，根据连接运算，可以定义前缀和后缀：

2. 幂（Power）

若将连接视为串的乘法运算，则定义串的幂运算为：

$$\left \{ \begin{aligned} s^0 &= \varepsilon \\ s^n &= s^{n-1}s, &n\geq 1 \end{aligned} \right .$$

故：

串$s$的$n$次幂实际上就是将$n$个$s$收尾相连的拼接起来，即：

2 文法

前面我们在数学上定义了语言学中的基本概念：字母表和串。接下来我们给出文法的形式化定义。

A. 自然语言的例子

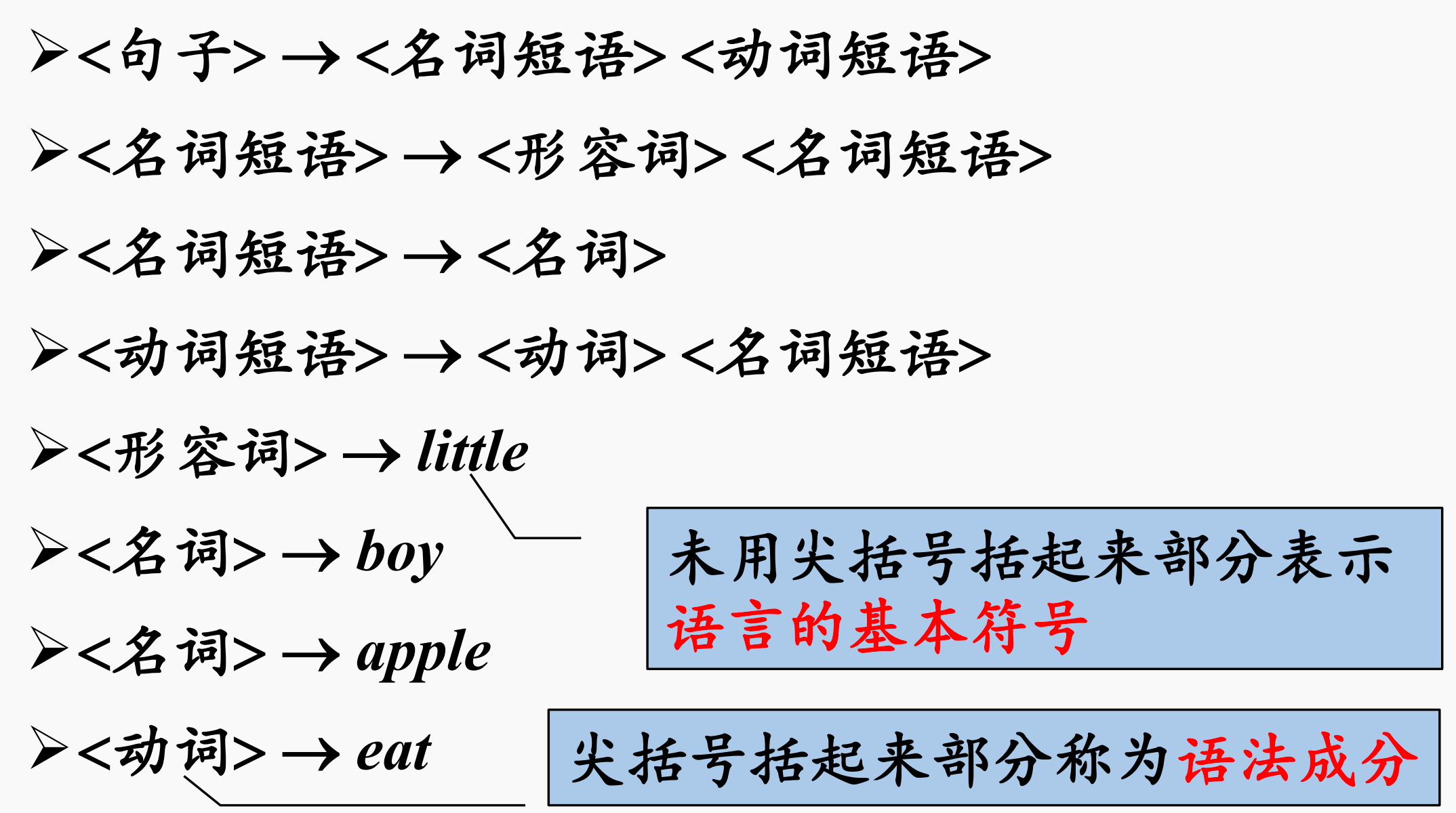
什么是文法？我们先给出一个简单版本的描述英文句子的文法

从这个文法中我们能看出：

• 一个英文句子是由一个名词短语加上一个动词短语组成的
• 一个名词短语可以由一个形容词加上一个名词短语组成的
• 一个名词短语也可以直接就是一个名词
• 一个动词短语可以是一个动词加上一个名词短语
• 形容词可以是little
• 名词可以是boy、apple
• 动词可以是eat

注意，实际的英文中还有状语短语、定义短语……，而且除了boy、apple以外还会有很多的名词。

但是这里，针对我们这里定义的little boy eat apple这句文法，只有动词短语和名词短语，名词只有boy、little

从上面这个例子中我们可以看出问文法的一些要素：

• 语法成分：例如动词短语、名词短语
• 基本符号：类似于apple、boy这样组成语言的最基本的要素
  • 如果这个文法是描述句子的语法规则的，那么这个文法的基本符号就是单词，例如我们这里的little boy eats apple
  • 如果这个文法是描述单词的构成规则的话，那么这个文法的基本符号就是字母

B. 文法的形式化定义

文法用大写字母$G$表示，定义文法$G$为一个四元组：

$$G=(V_T,V_N,P,S)$$

其中：

• $V_T$是终结符集合
• $V_N$是非终结符集合
• $P$是产生式集合
• $S$是开始符号

注意：

• $V_T\cap V_N=\emptyset$，$V_T\cup V_N$称为文法符号集

例如，我们定义一个算是表达式的文法：

其中，

• 终结符集合说明终结符可以是：标识符、加号、乘号、左括号、右括号
• 非终结符集合说明非终结符就是表达式
• 产生式集合说明了有四个产生式:：表达式加表达式等于表达式，表达式乘以表达式等于表达式，表达式加括号等于表达式，标识符是表达式
• 因为没有其他的语法成分，所以最大的语法成分（定义在非终结符中）就是表达式E

我们约定，在不引起歧义的前提下可以只写文法的产生式。故对于表达式的文法，有：

1) 终结符

终结符（Terminal Symbol）是文法所定义的语言的基本符号，有时也称为token。

例如上面吃苹果的英文句子文法的终结符有：boy、apple、eat和little。

因此，终结符集合的$V_T$的例子为：

2) 非终结符

非终结符（Non-Terminal）是用来表示语法成分的符号，有时也称为语法变量

例如上面吃苹果的英文句子文法的非终结符有：<句子>、<名词短语>、<动词短语>、<名词>、<形容词>、……

因此，非终结符集合的$V_N$的例子为：

3) 产生式

产生式（Production）描述了将终结符和非终结符组合成串的方法产生式的一般形式：

$$\alpha \rightarrow\beta$$

读作：$\alpha$定义为$\beta$

注意：

• $\alpha\in(V_T\cup V_N)^+$，即$\alpha$是定义在以终结符和非终结符作为符号的串。且长度至少为$1$，即必须要有元素。$\alpha$称为产生式的头部（head）或左部（left side）
• $\beta\in(V_T\cup V_N)^*$，即$\beta$是定义在以终结符和非终结符作为符号的串，可以是空串。$\beta$称为产生式的体（body）或右部（right side）

所以上面自然语言的例子，实际上就定义了很多个产生式

因此，产生式集合的例子为：

4) 开始符号

开始符号是一个特殊的非终结符，即$S\in V_N$。开始符号（Start Symbol）特指表示的是该文法中最大的语法成分。

例如，前面句子的例子中，开始符号是：

C. 产生式的简写

我们前面对文法进行了形式化的定义，具体来说，文法由终结符集合、非终结符集合、产生式集合和开始符号定义。

而在不引起歧义的情况下，可以只写出文法的产生式来表示文法。

但是在很多时候，产生式是具有共同的左部$\alpha$的。例如上面定义表示式的文法的产生式，左部均为$\alpha$。

此时，对一组有相同左部$\alpha$的产生式

$$\alpha \rightarrow \beta_1, \alpha \rightarrow \beta_2, \alpha \rightarrow \beta_3,\cdots,\alpha \rightarrow \beta_n$$

可以简写为：

$$\alpha \rightarrow \beta_1 | \beta_2 | \beta_3 | \cdots |\beta_n$$

读作：$\alpha$定义为$\beta_1$，或者$\beta_2$，……，或者$\beta_n$

此外，$\beta_1$、$\beta_2$、$\beta_3$、……、$\beta_n$称为$\alpha$的候选式（Candidate）

因此，上面定义表达式的文法的产生式可以简记为：

D. 符号约定

为了避免每次都要说明那些符号是终结符、那些符号是非终结符。

我们对终结符做出如下的约定：

我们对非终结符做出如下的约定：

最后，对文法符号、终结符号串和文法符号串做出如下的约定：

总结一下各种符号使用的约定：

3 语言

我们前面给出了文法的形式化定义，接下来我们给出语言的定义。

不过在给出语言的定义前，我们还是先从前面的例子出发，提出一个问题：

• 假设我们现在已经有了文法和一个串，如何判定这个串是否是满足文法的句子？

为了回答这个问题，我们首先需要讲解推导和归约。

A 推导 (Derivations）和规约（Reductions）

1) 推导的定义

我们首先给出推导的定义：

给定文法$G=(V_T, V_N, P, S)$，如果$α\rightarrow \beta \in P$，那么可以将符号串$\gamma\alpha\delta$中的$\alpha$替换为$\beta$，也就是说，将符号串$\gamma\alpha\delta$重写（rewrite）为$\gamma\alpha\delta$，记作

$$\gamma\alpha\delta \Rightarrow \gamma \beta\delta$$

此时，称文法中的符号串$\gamma\alpha\delta$直接推导（Directly Derive）出$\gamma\beta\delta$

• 简而言之，所谓推导其实就是将一个串中的产生式的左部替换为产生式的右部

2) n步推导

上面我们给出了推导的定义，接下来我们给出$n$步推导的定义：

如果$\alpha_0\Rightarrow \alpha_1$、$\alpha_1\Rightarrow \alpha_2$、$\alpha_2\Rightarrow \alpha_3$、……、$\alpha_n$则可以记为：

$$\alpha_0\Rightarrow \alpha_1 \Rightarrow \alpha_2 \Rightarrow \alpha_3 \Rightarrow\cdots\Rightarrow\alpha_n$$

称符号串$\alpha_0$经过$n$步推导出$\alpha_n$，可简记为$\alpha_0\Rightarrow^n \alpha_n$

由上述定义可知：

• $\alpha\Rightarrow^0 \alpha$
• $\Rightarrow^+$表示经过正数步推导（至少一步推导）
• $\Rightarrow^*$表示经过若干步推导（可以是零步推导）

3) 推导的例子

我们接下来举一个推导的例子。假设给定下述文法（注意，这里由于不会引起歧义，所以直接简写了生成式）：

那么给定一个串<句子>，我们可以进行如下的推导

注意，这里我们忽略动词单三的变化。

类似这样，从文法的开始符号开始，自顶向下的不断推导，最后会得到一个串

4) 规约

我们从文法的开始符号开始，不断用生成式的右部代替左部，最终得到一个串的方式称为推导。

类似的，我们从一个串开始，不断用生成式的左部代替右部，最终得到开始符号的方式称为规约

例如上面的例子：

因此，在讲解了推导和规约之后，回答前面的问题，有了文法（语言规则），如何判定某一词串是否是该语言的句子？

• 答，对句子进行规约，看能否将句子规约为开始符号

B 句型和句子

我们定义了推导和规约两种建立在文法上的操作后，我们接下来定义句型和句子。

1) 句型

定义：若$S\Rightarrow^ \alpha$，$\alpha\in(V_T\cup V_N)^$，则称$\alpha$是$G$的一个句型（Sentential Form）。

注意，

• 一个句型中既可以包含终结符，又可以包含非终结符，也可能是空串
• 即，句型可以全是语法成分，也可以部分含有语法成分，也可以不含有语法成分（空串或者句子）

2) 句子

定义：若$S\Rightarrow^ w$，$w\in V_T^$，则称$w$是$G$的一个句子（Sentence）。

注意，

• 句子是不包含非终结符的句型
• 即句子全是词语

3) 句型和句子的例子

我们还是举上面男孩吃苹果的例子来说明什么是句子，什么是句型。

根据上面的讲解，对男孩吃苹果这个文法，从开始符号<句子>开始进行一系列推导得到的所有对象都可以称为句型，但只有最后全部都是词语的才是句子。

C 语言

1) 语言的定义

我们定义了句子之后，接下来给出语言的形式化定义：

定义：由文法$G$的开始符号$S$推导出的所有句子构成的集合称为文法$G$生成的语言，记为$L(G)$。 即

$$L(G) = \{w|S\Rightarrow^*w, w\in V_T^*\}$$

注意，语言最大的好处就是，通过集合解决了无穷句子的问题。例如上面的表达式的文法，由表达式的文法就可以生成出语言，即所有的表达式。

而生成的句子可以是无穷多的。即表达式可以是无穷多的。

2) 举例

我们接下来举一个语言的例子。

定义文法$G$，求其生成的语言。

注意，为了讲清楚语言，我们需要搞明白所有的产生式。前面我们约定过。S表示开始符号，小写字母和数字表示终结符，大写字母表示非终结符。

所以：

• $S\rightarrow L|LT$是开始符号的产生式，表示开始符号可以被替换为语法变量L或LT

• $T\rightarrow L|D|TL|TD$是语法变量$T$的产生式，表示开头必须是字母，后面可以是字符或者数字的拼接

  

• $L\rightarrow a|b|c|…|z$表示$L$这个语法结构就是字母

• $D\rightarrow 0|1|…|9$表示$D$这个语法结构就是数字

而由于$S$开头必须是字母，所以实际上，上面的文法生成的语言是标识符

D 语言的运算

根据上面语言的定义，我们指导语言实际上就是一个句子的集合，所以类似字母表，我们可以定义语言上的运算：

注意，上面的例子中，语言$L$和语言$M$直接通过集合的形式给出了定义，所以每个元素其实都是一个句子，而非什么终结符、非终结符。

4 文法的分类

文法中最核心的就是产生式，因为产生式直接能够推导出语言。因此乔姆斯基根据对文法中产生式的不同要求，将文法分为了四种：

• 0型文法（Type-0 Grammar）
• 1型文法（Type-1 Grammar）
• 2型文法（Type-2 Grammar）
• 3型文法（Type-3 Grammar）

这一种文法分类体系，称为乔姆斯基文法分类体系

A. 0型文法/无限制文法 PSG

0型文法又称为无限制文法、短语结构文法（Phrase Structure Grammar, PSG），其实就是我们前面定义的文法。

这种文法对产生式几乎没有限制。只是要求产生式的左部$\alpha$中至少包含一个非终结符（语法结构），即：

$$\forall \alpha \rightarrow \beta \in P, \alpha中至少包含1个非终结符$$

由0型文法$G$生成的语言$L(G)$称为0型语言。

B. 1型文法/上下文有关文法 CSG

1型文法又称为上下文有关文法（Context-Sensitive Grammar, CSG），他要求产生式的左部$\alpha$中符号的个数必须小于右部$\beta$中符号的个数，即：

$$\forall \alpha \rightarrow \beta \in P, |\alpha|\leq |\beta|$$

注意：

• 根据前面对产生式左部和右部的定义：$\alpha\in(V_T\cup V_N)^+, \beta\in(V_T\cup V_N)^*$，因此$|\alpha|$最小为1，所以$\beta$不能为空串。即1型文法中不能包含空产生式 $$\alpha \rightarrow \varepsilon$$

此外，之所以称为上下文有关文法，是因为这类文法中产生式的一般形式为：

$$\alpha_1A\alpha_2\rightarrow\alpha_1\beta\alpha_2,\qquad \beta \neq\varepsilon$$

PS：注意，我们前面约定了前面的大写字母表示非终结符，所以这里的意思就是把一个语法结构进行展开

由上下文有关文法$G$生成的语言$L(G)$称为上下文有关语言（1型语言）

C. 2型文法/上下文无关文法 CFG

2型文法也称为上下文无关文法（Context-Free Grammar，CFG）

上下文无关文法要求每个产生式的左部$\alpha$必须是一个非终结符，即：

$$\forall \alpha \rightarrow \beta \in P, \alpha\in V_N$$

前面约定大写字母表示非终结符，所以2型文法的产生式一般形式为：

$$A\rightarrow \beta$$

前面举的标识符定义文法其实就是一个上下文无关文法，因为每个产生式左部都是一个非终结符

由上下文无关文法$G$生成的语言$L(G)$称为称为上下文无关语言

D 3型文法/正则文法 RG

3型文法又称为正则文法（Regular Grammer, RG），具体有两种：

• 右线性文法（Right Linear Grammer）：其生成式的通式为$A\rightarrow wB$或$A\rightarrow w$
• 左线性文法（Left Linear Grammer）：其生成式的通式为$A\rightarrow Bw$或$A\rightarrow w$

注意，我们在上面约定：

• 靠后的小写字母$u,v,w$表示终结符
• 考前的大写字母$A,B,C$表示非终结符

所以总的来说，正则文法表示产生式的右部至多只有一个终结符。

我们下买给出一个右线性文法的例子：

上面的文法所有的产生式左部都是非终结符，因此是一个2型文法。接着右部要么就是字母/数字，即终结符；要么就是在字母/数字右边加一个非终结符，因此是一个右线性文法。

生成式3、4和在一起说明了语法结构$T$是一个字母、数字的串，而再结合生成式1、2，则开始符号最后推导得到的句子是字母或者字母+字母数字串

因此实际上上面的文法最终定义的是一个标识符的生成语法。上面给出的这种定义标识符文法其实和前面的二型文法是等价的。

类似的，由正则文法$G$生成的语言$L(G)$称为正则语言

E 四种文法的关系

我们上面定义了四种文法，这四种文法的关系实际上是逐级限制的关系：

• 0型文法：$\alpha$中至少包含1个非终结符
• 1型文法/上下文有关文法，CSG：$|\alpha| \leq |\beta$
• 2型文法/上下文有关文法，CFG：$\alpha \in V_N$
• 3型文法/正则文法，RG：
  • $A\rightarrow wB$或$A\rightarrow w$
  • $A\rightarrow Bw$或$A\rightarrow w$

用图来表示的话，其实就是逐级包含的关系。

5 CFG的分析树

前面我们介绍了四种文法，其中：

• 正则文法可以用来描述程序设计中的绝大多数单词。但是正则文法生成的正则语言的生成能力有限，几乎无法生成程序设计语言中的句子

• 而上下文无关语法（CFG）可以描述绝大部分程序设计语言中的语法构造，因此也是被研究的最多的一类文法

因此，这一节主要介绍上下文无关语法的分析树

A 分析树的定义

我们在前面介绍过，分析树是用来描述句子结构的，我们也给出了直观的说明了什么是分析树，但是我们在第一章里没有给出分析树的定义。这里我们正式给出分析树的定义

分析树是指满足下面规则一个数：

• 树的根节点为文法开始符号
• 树内部结点表示对一个产生式$A\rightarrow \beta$的应用。父结点表示产生式左部$A$ 。子结点表示左到右构成的产生式的右部$\beta$
• 叶结点既可以是非终结符，也可以是终结符。从左到右排列叶节点得到的符号串称为是这棵树的产出（yield）或边缘（frontier）

例如下面的例子：

其中：

• 根节点是文法开始符号$E$
• 根节点（根节点是内部节点）表示第三个产生式的应用
• 根节点右孩子表示第四个产生式的应用

B 分析树是推导的图形化表示

我们上面介绍了推导。在给定文法的前提下，分析树其实就是推导的图形化表示，即：

$$给定一个推导S\Rightarrow \alpha_1\Rightarrow \alpha_2 \Rightarrow \alpha_3 \Rightarrow ... \Rightarrow \alpha_n ，对于推导过程中得到的每一个句型\alpha_i，都可以构造出一个边缘为\alpha_i的分析树$$

这句话的意思其实就是能够用分析树表示出所有的句子。

例如对于上面的文法，我们能够通过如下的推导得到句子：

那么对于这个推导过程，我们可以用下面的分析树表示：

观察这个分析树，就会发现，分析树的边缘其实就是句子

此外，注意：由于分析树是和推导一一对应的，因此同一个文法会有多个分析树。且一种推导会得到一种句型，因此分析树是和句型有对应关系的。

C. （句型的）短语

我们接下来给出短语的定义：

• 定义：给定一个句型，其分析树中的每一棵子树的边缘称为该句型的一个短语

我们前面介绍过句型，和分析树对应起来其实就是还没走到边缘的树的中间层。

还是前面的例子，给定下面的文法和一种分析树

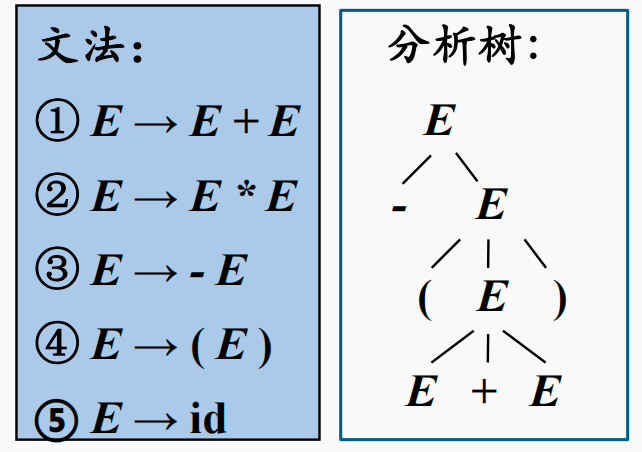
那么根据上面的短语的定义，以下都是这个分析树所对应的句型的短语：

• $-(E+E)$就是根节点为子树根节点的边缘
• $(E+E)$就是根节点右孩子为子树根节点的边缘
• $E+E$就是根节点右孩子的二孩子为子树根节点的边缘

在此基础上，如果子树只有父子两代结点，即子树高度为2，那么这棵子树的边缘称为该句型的一个直接短语。例如上面的例子中，直接短语是

注意，直接短语一定是某产生式的右部，但产生式的右部不一定是给定句型的直接短语。

我们举一个中文句子的例子。给定如下的文法：

假设输入下面这样的句子：

那么这个句子对应的分析树为：

由于提高、人民、生活、水平都是高度为2的子树的边缘，因此这四个词语都是直接短语。

但是高人、民生和活水虽然都是终结符，但并不是这个句子的直接短语。有可能是这个文法产生的其他句子的直接短语，例如：提高高人水平生活中高人就是直接短语

D. 二义性文法

如果一个文法可以为某个句子生成多棵分析树，则称这个文法是二义性的。

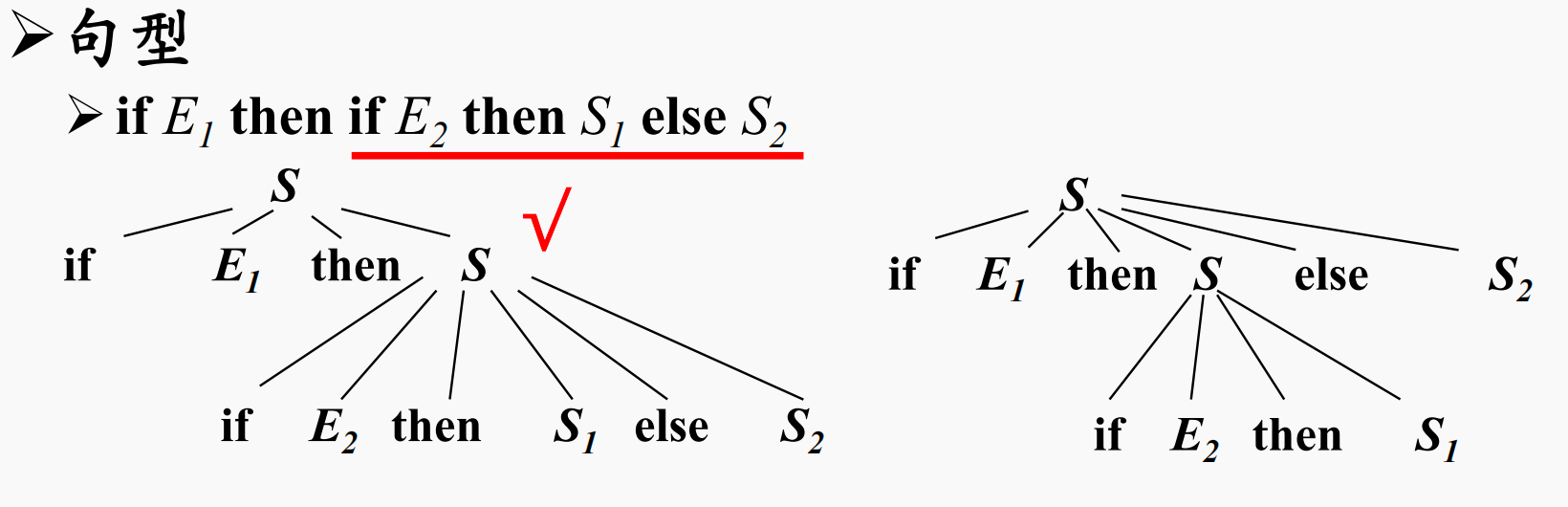
例如我们给定条件语句的文法

这个文法中定义了三个生成式：

• $S\rightarrow \mathrm{if}\ E\ \mathrm{then}\ S$
• $S\rightarrow \mathrm{if}\ E\ \mathrm{then}\ S\ \mathrm{else}\ S$
• $S\rightarrow others$

分别表示if、if ... else..语句

那么给定下面的句型，就能够构造出两种分析树

其实目前人类语言的语法大多数也是歧义的，但是作为编译器，因为要生成可执行代码，所以自然不希望编程语言中的句子是有歧义的。

为此，我们就需要去消除文法的二义性。但是消除文法的二义性是有代价的，例如：

• 引入新的非终结符
• 引入新的空产生式
• ……

不过我们下面介绍一种通常适用的消除二义性的方法，即引入消歧规则。

E. 消歧规则

对于一个二义性文法，在某些情况下可以定义一些特殊的规则消除歧义性，对应的规则称为消歧规则。

例如对于上面有歧义的句子，产生歧义的根源在于，句子中只有一个else，但是却有两个if。else即可以和第一个if匹配，也可以和第二个if匹配。

所以，这个时候我们可以添加一个规定：存在多个未匹配的if时，else和最近的if匹配。

通过引入的规定，我们此时相当于在两棵分析树中选择了第一棵分析树。

F. 二义性文法的判定

• 对于任意一个上下文无关文法，不存在一个算法，判定它是无二义性的
• 但能给出一组充分条件，满足这组充分条件的文法是无二义性的

也就是说，我们会给一组条件一、二、三：

• 满足条件一、二、三的文法必然是无二义性的
• 不同时满足条件一、二、三的文法不一定有二义性