GAMS教程 7：最佳匹配集合问题/分配问题

GAMS教程 7：最佳匹配集合问题

前面我们介绍了如何使用GAMS解决线性模型、时序模型。本文将介绍第三类模型，即网络模型。

网络模型中有很多的问题，今天讲介绍网络模型中的最佳匹配集合问题

1. 网络模型与最佳匹配集合问题

类似前面的时序模型，我们通过一个例子来引入网络模型。而后再介绍最佳匹配集合问题。其实最佳匹配集合问题就是分配问题。

A. 问题背景：作业分配问题

假设某门课上一共有五个学生，而老师一共布置了五个Project。每个学生对不同的项目有不同的喜好，这个喜好具体可以用0-10的preference score来衡量。0表示最不喜欢该项目，而10表示最喜欢该项目。

现在我们作为教师，希望能够通过合理的分配为每个学生分配一个项目，从而使得总体的满意度最高。

B. 问题抽象

描述满意度

我们接下来的第一个问题就是该如何描述学生对每个项目的满意度。

事实上，我们可以使用类似图表示函数的方式来表示学生对每个项目的满意度。例如下图

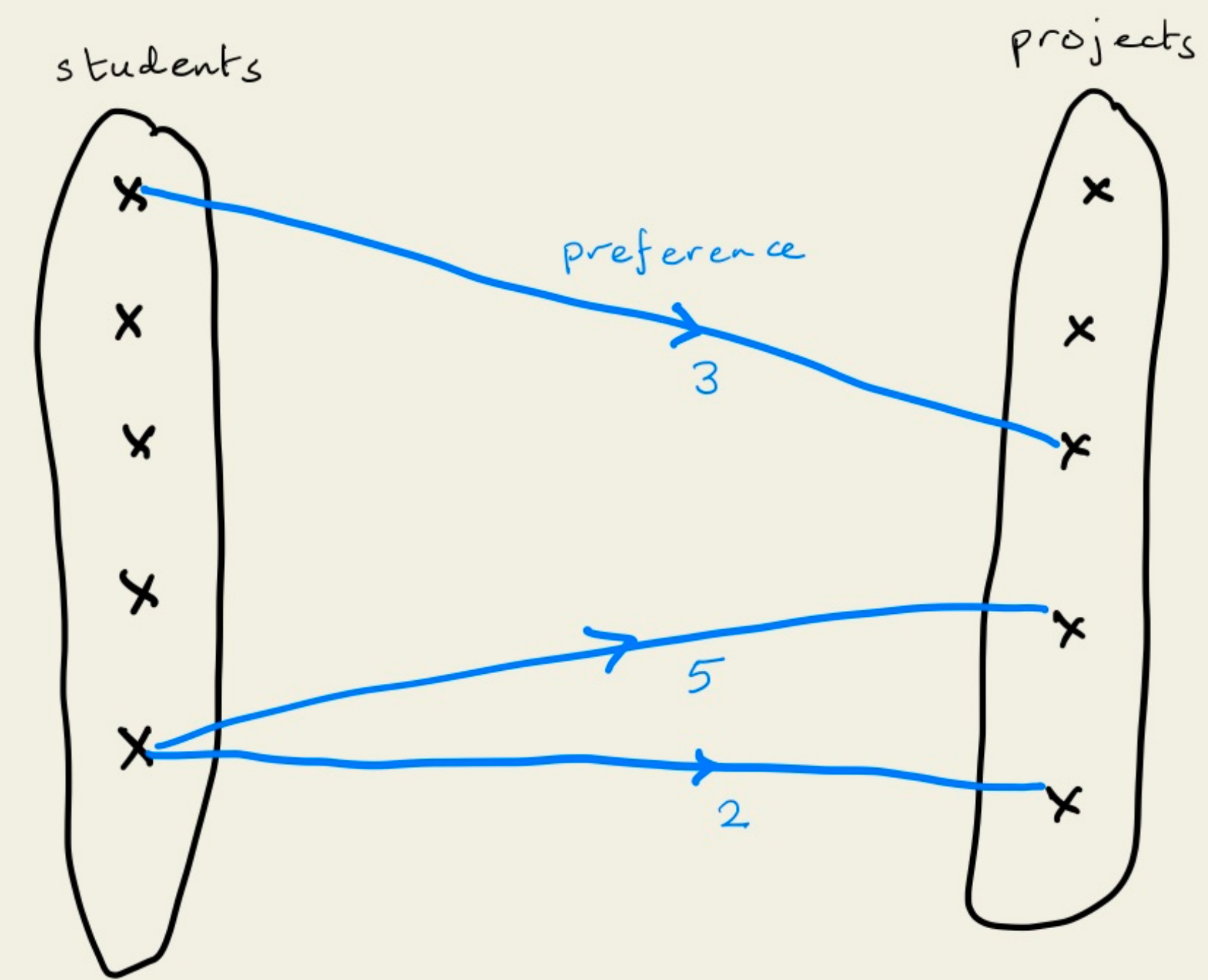
上图中：

• 我们把每个学生抽象为一个节点，把每个项目抽象为一个节点
• 我们把学生对项目的满意抽象为节点与检点之间的边

通过这种方式，我们就实现了用图来描述匹配问题。

因此，我们就可以使用一个矩阵来描述

$$c_{ij} = 学生i对项目j的偏好$$

其中：

• 集合$i$是学生集合，集合$j$是项目集合

描述分配关系

我们上面通过边表示了学生对每个项目的满意度，下面我们还需要描述项目的分配情况。

为此，我们也可以使用一个分配矩阵来描述，即

$$x_{ij}= \left \{ \begin{aligned} &1, &若学生i分配到了任务j\\ &0, &若学生i没分配到任务j \end{aligned} \right.$$

其中：

• 集合$i$是学生集合，集合$j$是项目集合

• 由于一个学生完成一个项目，因此存在下述约束

$$\begin{aligned} \sum_i x_{ij} &=& 1\\ \sum_j x_{ij} &=& 1 \end{aligned}$$

优化目标

我们的目标是最大化总体的满意度，因此优化目标为

$$\max \sum_{i\in I}\sum_{j\in J}c_{ij}x_{ij}$$

其中：

• $x_{ij}\in{0,1},i\in I, j\in J$

C. 数学模型

我们接下来综合上面的三个部分，得到作业分配问题的数学模型。

首先是决策变量，我们需要决定的就是那个作业被分配给那个学生，因此，决策变量其实就是

$$x_{ij}= \left \{ \begin{aligned} &1, &若学生i分配到了任务j\\ &0, &若学生i没分配到任务j \end{aligned} \right. \quad,\qquad\forall i\in I,\ \forall j\in J$$

而后是优化目标

$$\max \sum_{i\in I}\sum_{j\in J}c_{ij}x_{ij}$$

最后是约束

$$\begin{aligned} \sum_i x_{ij} &=& 1\\ \sum_j x_{ij} &=& 1 \end{aligned}$$

综合，我们的数学模型为

$$\max_{x_{ij}} \sum_{i\in I}\sum_{j\in J}c_{ij}x_{ij}\\ \left\{ \begin{array}{**lr**} \sum_i x_{ij} &=& 1\\ \sum_j x_{ij} &=& 1\\ x_{ij} &\in&\{0,1\} \end{array} \right.$$

D. 网络

我们上面虽然成功建立了作业分配问题的数学模型，但是我们到目前为止都不知道作业分配问题和网络模型以及最佳匹配集合问题之间的联系。

我们接下来首先给出网络在数学上的定义，而后介绍分配问题和网络之间的关系。

图的定义

定义：图 $G$ 是定义在结点集合 $V$ 和边集 $E\subseteq V\times V$，即 $G=(V,E)$

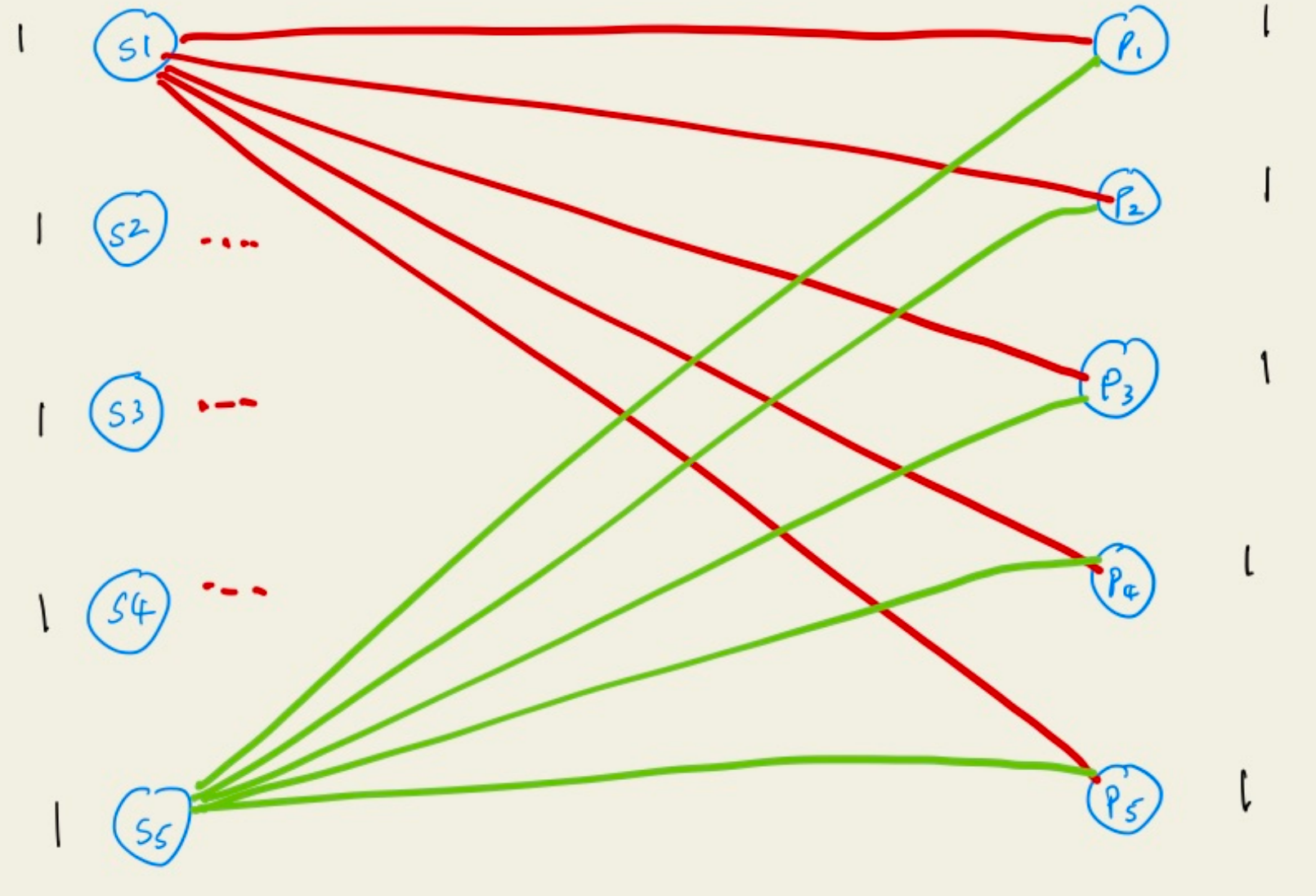
二分图的定义

二分图：图 $G=(V,E)$ 是一个二分图，若节点 $V$可以分为两个集合，即 $V=L\cup R$，使得所有的边都是在这两个集合间的，即

$$图G=(V,E)是二分图，当且仅当\\ \exists L,R, 使得,V=L\cup R, 且\\ e=(i,j)\in E\Rightarrow((i\in L)\cap (j\in R))\cup ((i\in R)\cap (j\in L))$$

因此，描述分配问题的图其实就是一个二分图。我们接下来将介绍网络的定义，并将分配问题与网络结合起来。

网络的定义

定义：网络 $G=(N,A)$ 是由一系列结点 $N$ 和弧 $A$ 所组成的图。

注意，当有方向的边(edge)成为弧(arc)，因此网络即有向图。

一个容量网络即指网络中的每一个弧 $a\in A$ 都有对应的容量 $u_a$

网络的描述：节点-边链接矩阵（Node-Arc Incidence Matrix）

我们可以用节点-边链接矩阵来描述一个网络，例如下面的网络

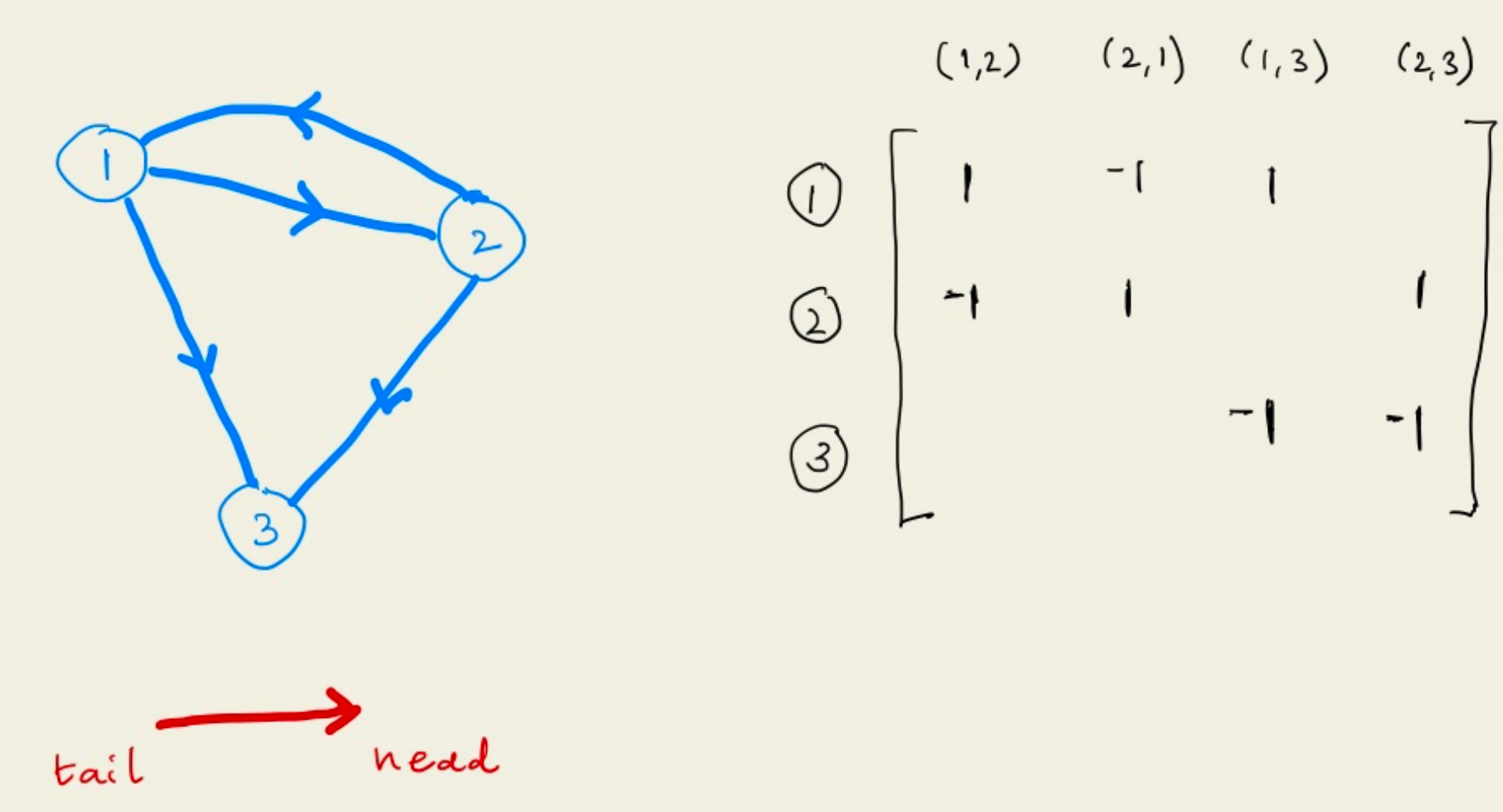
其中：

• 节点-边链接矩阵的行对应节点，而列对应所有的边。
• 节点-边链接矩阵中的每一行描述了对应节点连接情况
• 若边进入节点，则值为-1，若边从节点离开，则值为1
• 节点-边链接矩阵最大的形状是$n\times 2\cdot C_n^2$

匹配集合

匹配集合 $M\subseteq E$ 指的是对于结点集合 $V$ 中的每一个节点 $v$，$M$ 中至少有一个边是与节点 $v$ 连接的

而完美匹配集合指的是对于节点集合 $V$ 中的每一个节点 $v$，$M$ 中恰好有一个边是与节点 $v$ 连接

因此，作业分配问题其实就是在一个带权二分图中寻找到一个最大权的最佳匹配集合。

有很多算法都能解决任务分配问题，例如匈牙利算法，时间复杂度是$O(n^3)$。目前做的最好的算法的时间复杂度是$O(m+n^2)$。

2. GAMS求解网络模型

我们接下来讲解GAMS中如何求解网络模型

A. 数据声明

数据声明其实很简单，就是两个集合，分别对应学生和项目。然后还有学生对每个项目的满意度，是一个表格。

而决策变量$x_{ij}$要么就是1，要么就是0，因此是一个二元的变量。所以我们下面声明决策变量x是一个表格形式的变量

$title Assigning students to projects to maximize overall satisfaction

option limrow=0, limcol=0;


$onecho > cplex.opt
lpmethod 3
netfind 2
preind 0
$offecho

set projects/proj1*proj5/
    students/student1*student5/;

table preferences(students,projects)
             proj1     proj2     proj3     proj4    proj5
student1      7          6        5          8       9
student2      0          3        0          8       5
student3      0          0        0          4       3
student4      0          9        3          0       9
student5      0          6        7          6       0;

* want x to be 1 if that student is assigned to that project; 0 otherwise
* (actually in this simple assignment problem, dont need the variables to
* be binary)
binary variable x(students,projects);
variable satisfaction;

B. 约束声明

约束声明比较简单，就是求和等于1。决策变量的约束就是循环求和。

equations EQassignProjects(projects), EQassignStudents(students), objective;

* ensure that each project is assigned to one of the student
EQassignProjects(projects).. 
    sum(students, x(students,projects)) =e= 1;

* ensure that each students is assigned exactly one project
EQassignStudents(students)..  
    sum(projects, x(students,projects)) =e= 1;

* satisfaction index
objective..
  satisfaction =e= sum((students,projects),
    x(students,projects) * preferences(students,projects));

C. 模型声明与求解

最后，我们直接声明模型并求解

model  happyclass /EQassignProjects, EQassignStudents, objective/;

x.up(students,projects) = 1;
solve happyclass using mip maximizing satisfaction;

我们上面声明了x是binary的变量，所以其实没必要声明x的上界。

D. 综合

最后，我们求解网络模型的GAMS程序为

$title Assigning students to projects to maximize overall satisfaction

option limrow=0, limcol=0;

$ontext
A teacher wishes to assign 5 projects to 5 different students. Each
student has indicated their preference for each project by assigning it a
score between 0 and 10 (0 indicating strong dislike and 10 indicating
strong preference). The teacher wishes to make the assignment of projects
to students in a way that maximizes their overall satisfaction, as
measured by the sum of the preferences for the given assignments.
$offtext

$onecho > cplex.opt
lpmethod 3
netfind 2
preind 0
$offecho

set projects/proj1*proj5/
    students/student1*student5/;

table preferences(students,projects)
             proj1     proj2     proj3     proj4    proj5
student1      7          6        5          8       9
*student1      0          0        5.2        8.3     0
student2      0          3        0          8       5
student3      0          0        0          4       3
student4      0          9        3          0       9
student5      0          6        7          6       0;

* want x to be 1 if that student is assigned to that project; 0 otherwise
* (actually in this simple assignment problem, dont need the variables to
* be binary)
binary variable x(students,projects);
variable satisfaction;

equations EQassignProjects(projects), EQassignStudents(students), objective;

* ensure that each project is assigned to one of the student
EQassignProjects(projects).. sum(students, x(students,projects)) =e= 1;

* ensure that each students is assigned exactly one project
EQassignStudents(students)..  sum(projects, x(students,projects)) =e= 1;

* satisfaction index
objective..
  satisfaction =e= sum((students,projects),
    x(students,projects) * preferences(students,projects));

model  happyclass /EQassignProjects, EQassignStudents, objective/;

* happyclass.optfile = 1;
x.up(students,projects) = 1;
solve happyclass using mip maximizing satisfaction;