GAMS教程 5：时序模型

在很多优化模型中，我们都会遇到时序问题，即我们优化模型中的约束在每个月都有，而上个月的情况又会影响到下个月，例如工厂中上个月的原材料库存会影响到下个月的原材料进货。而我们的目标就是实现几个月内利润的最大化。

上个月的库存+本月产量=下个月库存+销售量

因此，时序模型作为一大类模型，本节就将对其进行讲解。

1. 时序模型

本节我么将以一个时序问题为例，讲解时序模型。

A. 问题背景Shoe Company

假设我们现在开着一家鞋业公司Shoe Company。在每个月，我们都会收到不同数量的订单，我们需要满足这些订单。而在此基础上，我们可以选择额外多生产一些鞋子，以减轻下个月的生产压力。

换而言之，每个月我们可以利用上个月剩余的未售出的鞋子与本月新生产出的鞋子一起进行销售以满足每个月收到的订单，但是每个月末存储一双鞋需要消耗$3元。

我们在每月开始的时候，可以花钱新雇佣工人以提升本月的产能。每生产一双鞋需要消耗4个工时以及$15元的材料费。

在月初新雇佣一个工人需要花费$1600，而在月末开除一位工人需要花费$2000。一位工人一个月的工资是$1500元，在此基础上工人每个月的工时是160小时。

如果正在赶做订单，我们可以要求工人加班，加班费是一个小时$13元，而每位工人一个月最多加班20小时。

本时序优化问题的Planning Horizon是4个月，即由我们决定四个月内，每个月鞋子的生产量、新雇佣工人的数量、开除的工人数量、储存的鞋子数量等等，最终的目的就是最小化开销。

B. 任务数据

问题中所有的数据如下

任务数据-1

任务数据-2

C. 数学模型

为了使用GAMS求解，我们首先需要写出上述任务的数学模型，而后使用GAMS进行求解

决策变量

问题的第一步就是确定问题的决策变量。一般来说，在一个复杂的问题中，这一步是最难的，因为我们往往无法准确的知道所有的决策变量，总是在建立数学模型的过程中才发现我们缺少某个决策变量。

这个问题中，我们需要决定的变量有：

每个月生产的鞋子
每个月末存储的鞋子
每个月初可用的工人
每个月加班总时长
每个月初新雇佣的工人数
每个月末开除的工人数

Shoe Company问题中的决策变量

目标变量：开销

假设四个月中，每个月生产$x_t$双鞋（$t\in{1,2,3,4}$）我们首先写出来任务中所有的开销项：

材料费：$\sum_{t\in T}\delta\cdot x_t$
工资：$\sum_{t\in T}\alpha\cdot w_t$
加班工资：$\sum_{t\in T}\beta\cdot o_t$
月初新雇佣开销：$\sum_{t\in T}\eta\cdot h_t$
月末开除开销：$\sum_{t\in T}\zeta\cdot f_t$
库存开销：$\sum_{t\in T}\iota I_t$

约束

我们写出了目标变量的计算式之后，接下来就要写出问题中的约束。

在这个时序问题中，尽管没有直接的约束，但是其实还是存在逻辑上的约束，具体来说，包括：

每个月生产使用的工时要小于总可用的工时

$ax_t \leq Hw_t +o_t$

每个月加班总工时要在允许范围内

$o_t \leq Ow_t$

每个月的需求必须被满足

$I_t \geq 0$

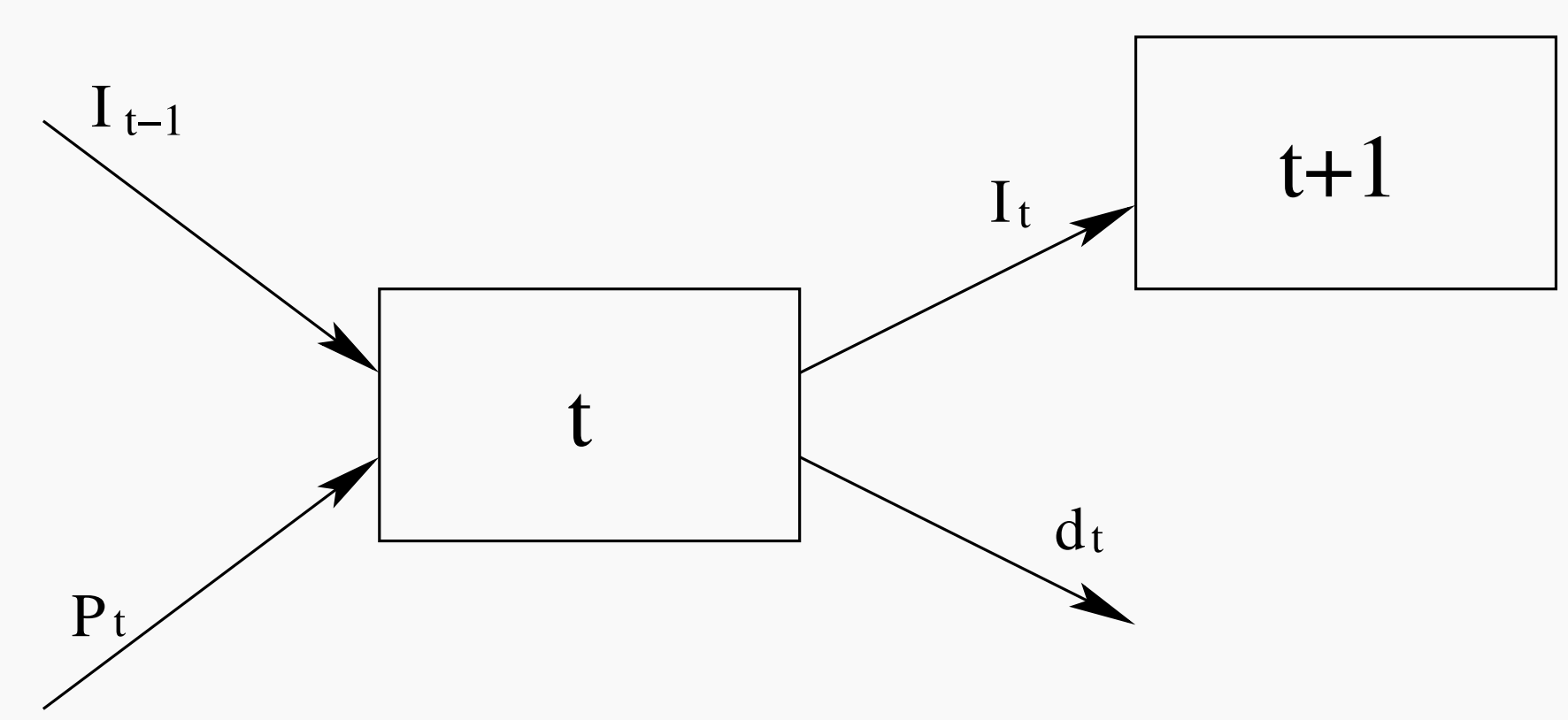
上个月初的库存+本月新生产 = 需求 + 下个月初的库存

$I_{t-1} + x_t = d_t +I_t,\ \forall t\in T$

本月可用工人 = 上个月可用工人 + 本月初新雇佣工人 - 上个月末开除工人

$w_t = w_{t-1}+h_t - f_t$

数学模型

综合上面目标变量和约束，我们可以得到Shoe Company问题的数学模型为

$\min_{t\in T}\sum(\delta\cdot x_t+\alpha\cdot w_t+\beta\cdot o_t+\eta\cdot h_t+\zeta\cdot f_t+\iota \cdot I_t)\\ \left\{ \begin{array}{**lr**} ax_t &\leq& Hw_t +o_t\\ o_t &\leq& Ow_t\\ I_t &\geq& 0\\ I_{t-1} + x_t &=& d_t +I_t\\ w_t &=& w_{t-1}+h_t - f_t\\ I_0&=&\mathcal{I}_0\\ w_0 &=& \mathcal{W}_0 \end{array} \right.$

2. GAMS实现

接下来，我们就要使用GAMS去实现一下上述的时序模型了。

A. 数据声明

首先是数据声明部分，包括Scalar、Parameter、Table、Set以及Variable在内的。

和前面一样，为了实现数据和模型的分离，还是把所有的数据声明放在一个.inc文件里

* shoeco.inc
parameter d / Jan 3000, Feb 5000, Mar 2000, Apr 1000/;

I0 = 500;
W0 = 100;
alpha = 1500;
MAXH = 160;
MAXO = 20;
beta = 13;
a = 4;
delta = 15;
eta = 1600;
zeta = 2000;
iota = 3;

而后，在shoeco.gams的开头部分声明剩余的数据

$title ShoeCo Aggregate Planning Model.

set T;

scalars
    I0      Initial Inventory
    W0      Initial Number of Workers
    alpha   Dollars per month for worker
    beta    Dollars per hour for overtime
    MAXH    max hours per month
    MAXO    max overtime hours per month
    a       labor hours per shoe
    delta   Raw material costs (dollars) per shoe
    eta     hiring cost (dollars) per worker
    zeta    firing cost (dollars) per worker
    iota    inventory cost (dollars) per shoe
;

parameters
    d(T<)    Demand
;

* Now assign all the data
$include shoeco.inc

display T;

positive variables
    x(T)    Production in period T
    I(T)    Ending inventory in period T
    w(T)    Worker level at end of period T
    h(T)    Number of workers hired at beginning of T
    f(T)    Number of workers fired at beginning of T
    o(T)    Number of overtime hours in period T
;

free variable cost;

B. 约束

对于约束，其实有两个小问题：

约束个数问题
边界问题

约束个数问题

我们上面得到的优化模型的约束如下

$\left\{ \begin{array}{**lr**} ax_t &\leq& Hw_t +o_t\\ o_t &\leq& Ow_t\\ I_t &\geq& 0\\ I_{t-1} + x_t &=& d_t +I_t\\ w_t &=& w_{t-1}+h_t - f_t\\ \end{array} \right.$

这五项都是和时间$t$有关的，每个月都有一个约束。注意，第三个约束其实规定了下届，所以等下用.lo去处理。因此我们把四个月都算上的话，其实四个约束能展开成16个约束。

但是因为都是和时间有关的，所以我们其实可以把每个约束都声明成为一个矩阵约束。例如对于第一个约束来说，四个约束展开就是：

$\left\{ \begin{array}{**lr**} ax_1 &\leq& Hw_1 + o_1\\ ax_2 &\leq& Hw_2 + o_2\\ ax_3 &\leq& Hw_3 + o_3\\ ax_4 &\leq& Hw_4 + o_4\\ \end{array} \right. \\ \Updownarrow \\ a\cdot \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} \leq H\cdot \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ w_4 \end{bmatrix} + \begin{bmatrix} o_1 \\ o_2 \\ o_3 \\ o_4 \end{bmatrix}$

因此这四个约束其实可以直接写成一个矩阵约束，即

Set T /Jan, Feb, Mar, Apr/;
Variable X(T);

equation constraion1(T);

同理，剩下的三个约束都是矩阵约束，故有

set T /Jan, Feb, Mar, Apr/;

equations
    RegLabor_eq(T)
    OverLabor_eq(T)
    BalShoe_eq(T)
    BalPeople_eq(T)
;

边界问题

我们所有的约束中有两个等式，一个是库存的等式，一个是工人的等式，即BalShoe_eq和BalPeople_eq。这两个等式虽然说都是矩阵约束，但是这两个约束在边界上存在问题。

具体来说就是在第一个月的时候，这两个约束是

$\left\{ \begin{array}{**lr**} I_{0} + x_1 &=& d_1 +I_1\\ w_1 &=& w_{0} + h_1 - f_1\\ \end{array} \right.$

可是$I_0$和$w_0$是两个Scalar，并不属于Variable I(T)和w(T)中。因此在第一个月，这两个约束和剩下月份的约束不同。

为此，这两个约束可以这样写

BalShoe_eq(T)..
    I0$(ord(T) eq 1) + I(T-1) + x(T) =E= d(T) + I(T) ;

BalPeople_eq(T)..
    W0$(ord(T) eq 1) + w(T-1) + h(T) =E=  w(T) + f(T) ;

C. 综合

综上，针对Shoe Company问题的GAMS程序为

* shoeco.inc
parameter d / Jan 3000, Feb 5000, Mar 2000, Apr 1000/;

I0 = 500;
W0 = 100;
alpha = 1500;
MAXH = 160;
MAXO = 20;
beta = 13;
a = 4;
delta = 15;
eta = 1600;
zeta = 2000;
iota = 3;

* shoeco.gms

$title ShoeCo Aggregate Planning Model.

option limrow = 50, limcol = 0 ;

set T;

scalars
    I0      Initial Inventory
    W0      Initial Number of Workers
    alpha   Dollars per month for worker
    beta    Dollars per hour for overtime
    MAXH    max hours per month
    MAXO    max overtime hours per month
    a       labor hours per shoe
    delta   Raw material costs (dollars) per shoe
    eta     hiring cost (dollars) per worker
    zeta    firing cost (dollars) per worker
    iota    inventory cost (dollars) per shoe
;


parameters
    d(T<)    Demand
;

* Now assign all the data
$include shoeco.inc

display T;

positive variables
    x(T)    Production in period T
    I(T)    Ending inventory in period T
    w(T)    Worker level at end of period T
    h(T)    Number of workers hired at beginning of T
    f(T)    Number of workers fired at beginning of T
    o(T)    Number of overtime hours in period T
;

free variable cost;

equations
    cost_eq
    RegLabor_eq(T)
    OverLabor_eq(T)
    BalShoe_eq(T)
    BalPeople_eq(T)
;

cost_eq..
    cost =E= sum(T, delta*x(T) + alpha * w(T) + beta * o(T) + eta * h(T) +
                    zeta * f(T) + iota * I(t)) ;

RegLabor_eq(T)..
    a*x(T) =L= MAXH * w(T) + o(T) ;

OverLabor_eq(T)..
    o(T) =L= MAXO*w(T) ;

BalShoe_eq(T)..
    I0$(ord(T) eq 1) + I(T-1) + x(T) =E= d(T) + I(T) ;

BalPeople_eq(T)..
    W0$(ord(T) eq 1) + w(T-1) + h(T) =E=  w(T) + f(T) ;

model shoeco /all/;
* d(T) = 2*d(T);
solve shoeco minimizing cost using lp;

display x.l, I.l, w.l, h.l, f.l, o.l;