GAMS教程 4：线性模型

GAMS
GAMS
发布日期:   2022-10-16
更新日期:   2023-06-01
文章字数:   2.4k
阅读时长:   11 分
阅读次数:  

线性模型

GAMS教程 4：线性模型

在前面的几讲中，我们讲解了GAMS的基础知识，也仅限于GAMS中的基础知识。但事实上，GAMS作为一个工具，我们使用GAMS是为了求解优化问题。

因此，我们关于GAMS，其实要学习的内容包括两部分：

  • 第一部分是GAMS的基础知识，包括语法、程序结构等等
  • 第二部分是如何使用GAMS求解优化问题的知识

从本节开始，我们就将关注与第二部分，即讲解如何使用GAMS求解优化问题。

本节，我们就将讲解线性模型。我们首先给出线性模型的定义和几个特征（属性），而后再举几个线性模型的例子以及如何用GAMS求解线性模型。

1. 线性模型

A. 定义

线性模型指的是模型中的约束都是线性的优化模型。

用数学语言来描述，就是仅包含线性等式约束和线性不等式约束的优化模型

线性等式约束

线性等式约束的定义如下：

线性不等式约束

线性不等式约束的定义如下

B. 线性模型的特征

线性模型具有以下的特征：

  • Proportionality： Inputs/outputs/costs must keep same proportions as levels change
  • Additivity： The activites (production amounts. etc), are an additive (linear) function of the input variables
  • Divisibility：The activity can be operated at any real level between upper and lower bounds (if any)

2. 使用GAMS解决线性模型

我们接下来举几个GAMS解决线性模型的例子。

A. TopBrass Company

第一个例子就是在前言中介绍的为TopBrass Company制作奖杯的问题

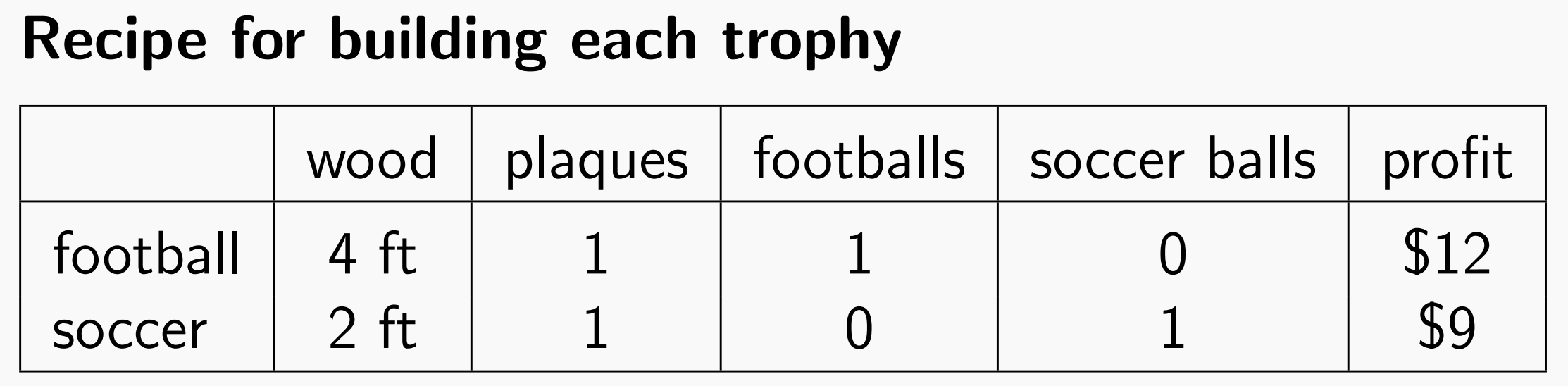
Top Brass Trophy Company是一家专门生产奖杯的公司，这家公司生产两种奖杯：

  • 足球奖杯（Soccer）
  • 橄榄球奖杯（Football）

卖出一个橄榄球奖杯将会获得$12的利润，而卖出一个足球奖杯将会获得$9元的利润。而生产一个奖杯，两种奖杯分别需要消耗：

  • 木质底座：橄榄球奖杯需要4平方英寸大小的木板，足球奖杯需要2平方英尺的奖杯
  • 奖杯体：各消耗一个
  • 顶端的标志物：橄榄球顶端有一个铜制橄榄球，而足球奖杯顶端有一个铜制足球。

假设目前库存的原材料为：

  • 1000个黄铜橄榄球
  • 1500个黄铜足球
  • 1750个奖杯体
  • 4900平方英寸的木板

假设制作的所有奖杯都能够售出，那么Top Brass Trophy Company能够获得的最大利润是多少？

制作所需的材料表

库存的原材料

通常，我们在求解线性问题的时候，最好先列出线性问题的数学模型。

而TopBrass Company问题中的数学模型如下

该优化问题中，决策变量是$f$和$s$，目标变量是$p$，因此我们一共要声明三个变量。

此外，优化问题一共有7个约束。但是7个约束中的四个约束其实都是针对变量$f$和$s$的范围进行的约束，因此对于这四个约束，可以使用变量的属性来进行声明，即.lo和.up属性来声明变量的上下限。所以，我们一共需要声明三个equation。

由于有三个约束，因此就需要三个参数（Parameter）。但是由于f+s的参数都是1，所以其实只需要两个参数即可。

因此，对于这个优化问题我们最终的解如下

* Top Brass 4 介绍了Parameter，Scalar，针对Parameter的Sum操作以及集合中元素的属性

set I/football, soccer/;

free variable profit "total profit";

positive variables
x(I) "trophies";

parameters
  profitMargin(I) / "football" 12 , "soccer" 9 /
  boardFeet(I)    / "football"  4 , "soccer" 2 /
  plaques(I)      / "football"  1 , "soccer" 1 /;

scalar
  plaquesMax /1750/
  woodMax    /4800/
  footballMax /1000/
  soccerMax /1500/;

equations
  obj    "max total profit"
  plaq   "bound on the number of plaques to be used",
  wood   "bound on the amount of wood to be used";

obj..
  profit =e= sum(I, profitMargin(I)*x(I));

plaq..
  sum(I,plaques(I)*x(I)) =l= plaquesMax;

wood..
  sum(I,boardFeet(I)*x(I)) =l= woodMax;

model topbrass /all/;

x.up("football") = footballMax;
x.up("soccer") = soccerMax;

solve topbrass using lp maximizing profit;

parameter pct(I) "holds the final percentages";
alias (I,J);

pct(I) = 100 * x.l(I)  / (sum(J,x.l(J)));
display pct;

当然，我们可以把两个参数（Parameter）集合起来，组成一个表格（Table）。然后我们就把两个资源限制的公式集合起来。具体代码如下：

$title Top Brass (LP) Example 5.1 of Rardin (1998)  (modified)

option limrow = 0, limcol = 0;
option solprint=off;

set I /football,soccer/;
set R /plaques,wood/;

table a(R,I)  "Per-Unit resource requirements"
         football   soccer
plaques     1         1
wood        4         2  ;

parameters
    c(I) / "football" 12 , "soccer" 9 /
    u(I) / "football" 1000 , "soccer"  1500 /
    b(R) / "plaques"  1750,  "wood"  4800 /;

free variable profit "total profit";

positive variables
x(I)     "number trophies" ;

equations
    profit_eq         "profit definition"
    resource_con(R)   "resource limit" ;

profit_eq..
  profit =E= sum(I,c(I)*x(I));

resource_con(R)..
  sum(I, a(R,I)*x(I)) =L= b(R);

x.up(I) = u(I);

model btb /all/;

solve btb using lp maximizing profit;

parameter pct(I) "holds the final percentages";
alias (I,J);

pct(I) = 100 * x.l(I)  / sum(J, x.l(J))
display pct;

B. BigTop Brass

在TopBrass问题中，我们只有两种奖杯、三种资源。如果我们把问题的规模在扩大一下，变成20种奖杯、200种资源呢？此时问题就会非常非常大，我们基本上没法手动解决。

所以在这种时候，我们必须要用GAMS来帮助我们解决问题。

我们可以把数据声明单独写成一个文件.inc文件

* bigtopbrass.inc
set I /football,soccer/;
set R /plaques,wood/;

table a(R,I)  "Per-Unit resource requirements"
         football   soccer
plaques     1         1
wood        4         2  ;

parameters
    c(I) / "football" 12 , "soccer" 9 /
    u(I) / "football" 1000 , "soccer"  1500 /
    b(R) / "plaques"  1750,  "wood"  4800 /
;

然后再描述模型的.gams文件中include数据声明文件

$ondollar
$title Big Top Brass (LP)


$include bigtopbrass-1.inc
free variable profit "total profit";

positive variables
x(I)     "number trophies" ;

equations
profit_eq         "profit definition"
resource_con(R)   "resource limit" ;

profit_eq..
  profit =E= sum(I,c(I)*x(I));

resource_con(R)..
  sum(I, a(R,I)*x(I)) =L= b(R);

x.up(I) = u(I);

model btb /all/;

solve btb using lp maximizing profit;

display x.l;

C. McGrease营养问题

通常人们认为快餐是不营养的，但是快餐的味道却非常好。不巧的是，美国有非常多的快餐。而McGrease问题研究的就是对于麦当劳中的每种食物，我们该如何吃、吃出什么样的配比才能够保证我们营养的同时开销最小。

假设现在一共有以下几种麦当劳的食物（都是美国这里的麦当劳经典款）

QP: Quarter Pounder // 牛肉汉堡

MD: McLean Deluxe // 另一种汉堡

BM: Big Mac // 双层牛肉堡

FF: Filet-O-Fish // 鳕鱼堡

MC: McGrilled Chicken // 麦乐鸡

FR: Small Fries // 薯条

SM: Sausage McMuffiffiffin // 下午茶的香肠

1M: 1% Milk // 牛奶

OJ: Orange Juice // 橙汁

而我们需要的营养有以下几种

Prot: Protein

VitA: Vitamin A

VitC: Vitamin C

Calc: Calcium

Iron: Iron

Cals: Calories

Carb: Carbohydrates

而每种食物各种营养成分的含量、价格以及我们需要的营养成分如下

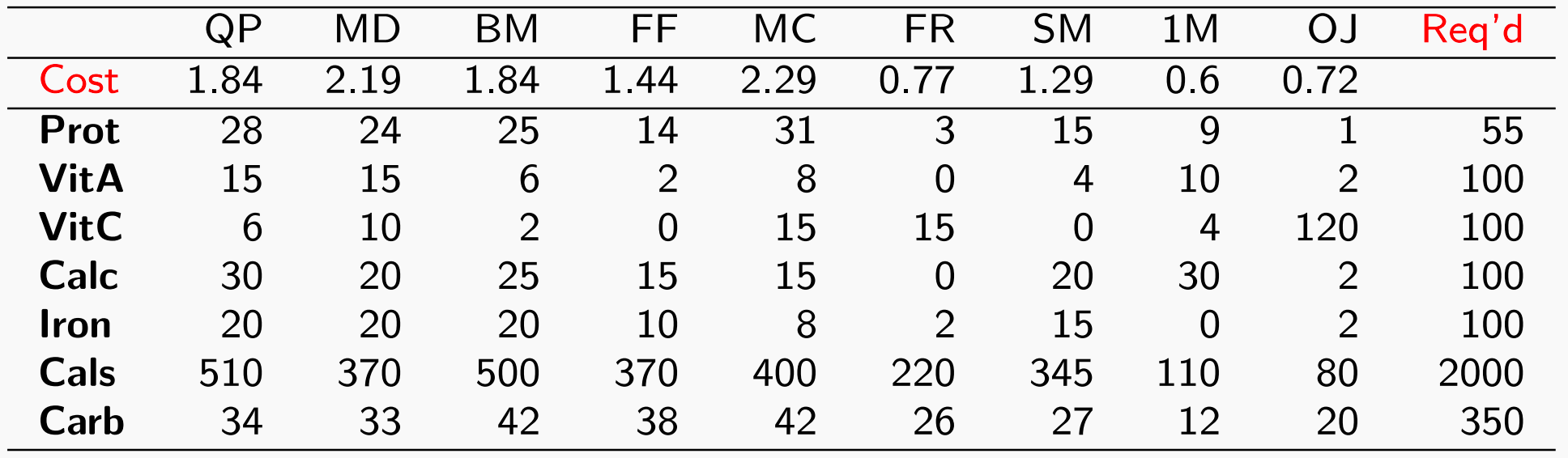
价格、营养成分表

拿到一个优化问题后，我们首先需要考虑的就是确定决策变量和优化目标，而后才是问题中的优化目标。

McGrease问题中的决策变量就是九种食物每种事物的食用量，而目标变量就是总价，约束就是每种食物提供的营养的总和。

所以上面的优化问题的数学描述为：

我们使用如下的记号，以简化问题

问题的记号

则McGrease问题可以简化为下述形式

McGrease问题

这就是典型的一个优化问题

而对McGrease问题进行求解的GAMS程序为

$title McGreasy Diet Problem

option limrow=10, limcol=0;

set food /QP, MD, BM, FF, MC, FR, SM, 1M, OJ/;
set nutr /Prot, VitA, VitC, Calc, Iron, Cals, Carb/;

table a(nutr,food)  per unit nutrients
        QP  MD  BM  FF  MC  FR  SM  1M   OJ
Prot    28  24  25  14  31   3  15   9    1
VitA    15  15   6   2   8   0   4  10    2
VitC     6  10   2   0  15  15   0   4  120
Calc    30  20  25  15  15   0  20  30    2
Iron    20  20  20  10   8   2  15   0    2
Cals   510 370 500 370 400 220 345 110   80
Carb    34  33  42  38  42  26  27  12   20
;


parameter 
        min_nutr(nutr) /Prot 55, VitA 100, VitC 100, Calc 100, Iron 100, Cals 2000, Carb 350 /;

parameter
        cost(food) /QP 1.84, MD 2.19, BM 1.84, FF 1.44, MC 2.29, FR 0.77, SM 1.29, 1M 0.6, OJ 0.72 /;

free variables
    total_cost  Total Cost of Daily Diet
;

positive variables
    x(food)     Number of each type of food to eat
;


equations
    cost_eqn        Define Objective
    min_nutr_eqn(nutr)    Minimum Daily Requirement
;


min_nutr_eqn(nutr)..
    sum(food,a(nutr,food)*x(food)) =G= min_nutr(nutr) ;

cost_eqn..
    total_cost =E= sum(food,cost(food)*x(food)) ;


model diet1 /cost_eqn, min_nutr_eqn/;
solve diet1 using lp min total_cost;

display x.l;
文章作者: Jack Wang
文章链接: https://jackwang0107.github.io/2022/10/16/gams-jiao-cheng-4-xian-xing-mo-xing/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Jack Wang !
GAMS
赏
  目录