GAMS教程 1：数据类型及程序结构

1. GAMS的数据类型

GAMS中一种有5种数据类型，分别是：

• 集合（Set)
• 参数（Parameter）
• 标量（Scalar）
• 变量（Variable）
• 表格（Table）

其中：

• 标量是一种独立的数据类型
• 参数、变量和列表具有相互依赖关系

而由于变量是特殊的数据类型，因此下面将单独变量。

A. 集合（Set）

集合是GAMS中最基础的数据类型，其他的数据类型，例如参数、变量和表格都依赖于集合。

集合的声明

数学上我们按照下面的方式声明一个集合

$$S = \{a,b,c\}$$

而在GAMS中，我们按照下面的方式声明一个集合

Set S / a, b, c /;

详细的声明规则如下

Set[s] set_name ["text"] [/element [text] {,element [text]} /]
     {,set_name ["text"] [/element [text] {,element [text]} /] } ;

其中：

• text表示注释，如果我们为集合整体注释的话，必须要加""，但是为集合中的元素注释则不需要
• []表示可选项，因此在声明集合的时刻可以只声明集合的名称，而不用声明集合中的元素，也可以不用对集合整体或者每个元素进行注释
• {}表示可重复项
• 我们可以同时声明多个集合，如果声明多个集合的话，就必须使用Sets

通常来说，我们认识中的集合的作用就是收集并保存一堆元素。GAMS中的集合更多的其实起着数组下标的作用，每个元素没有具体得数值。关于这个作用在稍后的参数和表格中会涉及到。

一个集合的例子为

Set letters /a, b, c, d/;

Sets numbers /1, 2, 3, 4, 5/,
     cities "我去过的   所有城市"
            / Edmonton  "2019去的埃德蒙顿", Xian  "2021年在西安读大学", Madison  "2022年在麦迪逊交换"/;


display letters, numbers, cities;

需要注意的是：

• GAMS语言和一般的编程语言不同，GAMS变成语言并没有整数、浮点书、字符串这些数据类型，在GAMS看来，他们都是element

• display类似于printf，即输出变量的值。

运行后lst文件中的结果表明，我们在第8行输出了前面定义的三个集合

B. 参数（Parameter）

上面我们说过，GAMS中的集合起着数组下标的作用，那么GAMS中的参数其实起着数组的作用。一般来说，我们的模型中约束的系数就保存在参数这个数据结构中。既然参数更多起着数组的作用，那么参数可以声明，可以赋值也可以取值。我们下面先介绍参数的声明，然后再介绍参数的赋值与取值。

参数的声明

声明Parameter数据类型的语法如下

parameter[s] param_name[(index_list)] [text] [/ element [=] numerical_value
                                              {,element [=] numerical_value} /]
           {,param_name[(index_list)] [text] [/ element [=] numerical_value
                                              {,element [=] numerical_value} /]} ;

其中：

• []是可选项，text是注释，{}表示可重复项
• index_list表示选用做下标的集合
• 需要注意，element必须是索引集合中的元素，numerical_value必须是可以解释的数值，要么是字面量的数值，要么是稍后介绍的标量，要么是稍后介绍的参数、表格的取值。

声明参数的例子如下

Set letters /a, b, c, d/;

Sets numbers /1, 2, 3, 4, 5/,
     cities "我去过的   所有城市"
            / Edmonton  "2019去的埃德蒙顿", Xian  "2021年在西安读大学", Madison  "2022年在麦迪逊交换"/;


Parameters
    param_letter(letters)   "以letters集合作为索引集合的参数"
        / a    1, b    2, c    3, d    4 /,

    param_num(numbers)      "以numbers集合作为索引集合的参数"
        / 1 = 11, 2 = 12, 3 = 13, 4 = 14, 5 = 15 /,

    param_city(cities)      "以cities集合作为索引集合的参数"
        / Edmonton   2019, Xian = 2021/;


display letters, param_letter;
display numbers, param_num;
display cities, param_city;

其中：

• 我们对param_letter和param_num这两个参数在声明的时候就进行了初始化，即为每一个下标赋值
• param_city参数只进行了部分赋值

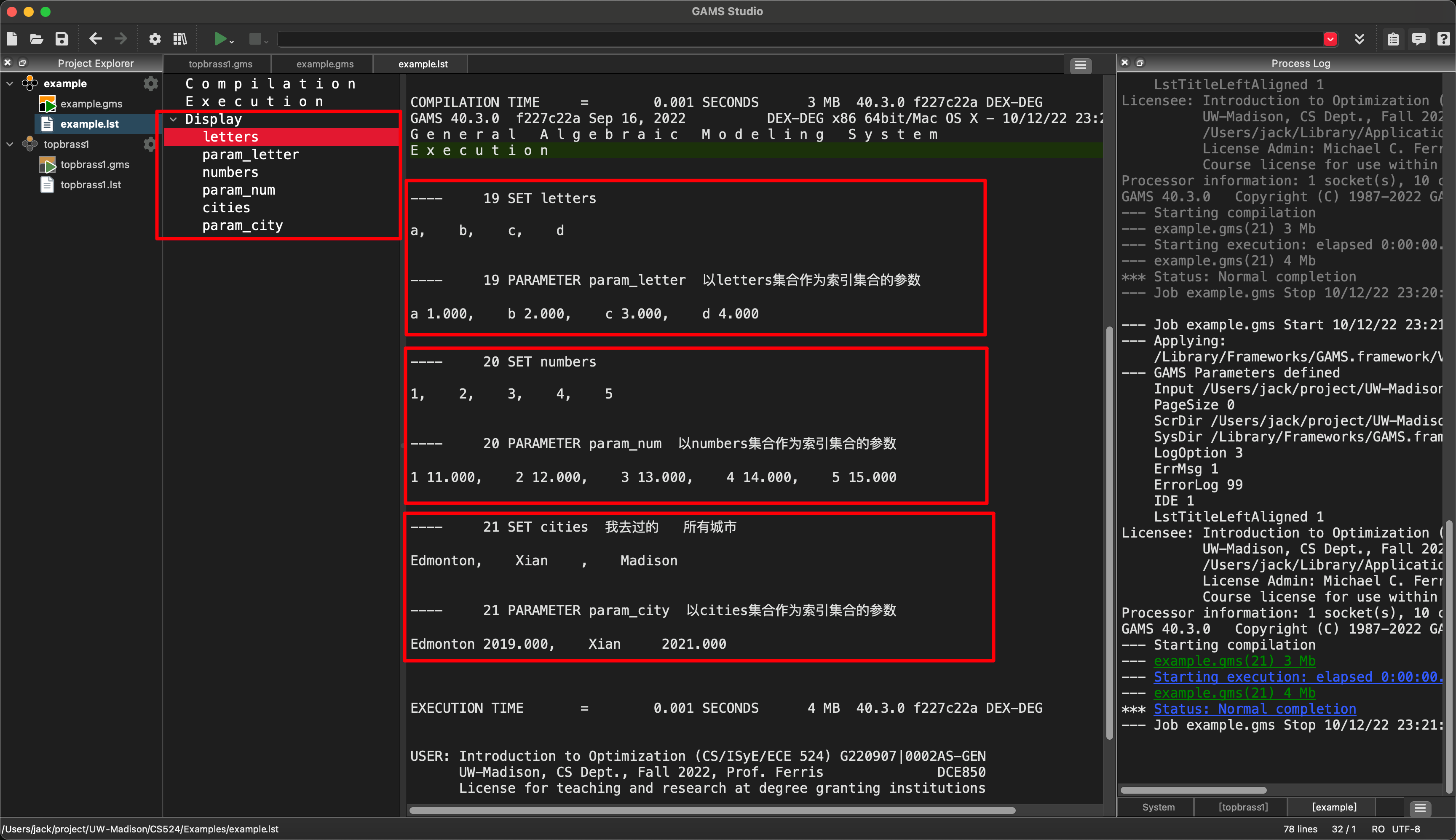
运行之后的结果中需要注意的是：

• 每一个数值
• param_city中只有Edmonton和Xian这两个下标有值

参数的赋值

我们其实可以在参数初始化借助之后单独对某些下标赋值，语法如下

prameter_name('element') = neumerical_value;

注意：

• element的值必须是在索引集合中的元素
• neumerical_value必须是可以解释的数值，包括整数和浮点数

继续利用上面的那个例子，为param_city中的Madison这个元素赋值

Set letters /a, b, c, d/;

Sets numbers /1, 2, 3, 4, 5/,
     cities "我去过的   所有城市"
            / Edmonton  "2019去的埃德蒙顿", Xian  "2021年在西安读大学", Madison  "2022年在麦迪逊交换"/;


Parameters
    param_letter(letters)   "以letters集合作为索引集合的参数"
        / a    1, b    2, c    3, d    4 /,

    param_num(numbers)      "以numbers集合作为索引集合的参数"
        / 1 = 11, 2 = 12, 3 = 13, 4 = 14, 5 = 15 /,

    param_city(cities)      "以cities集合作为索引集合的参数"
        / Edmonton   2019, Xian = 2021/;


param_city('Madison') = 2022;


display letters, param_letter;
display numbers, param_num;
display cities, param_city;

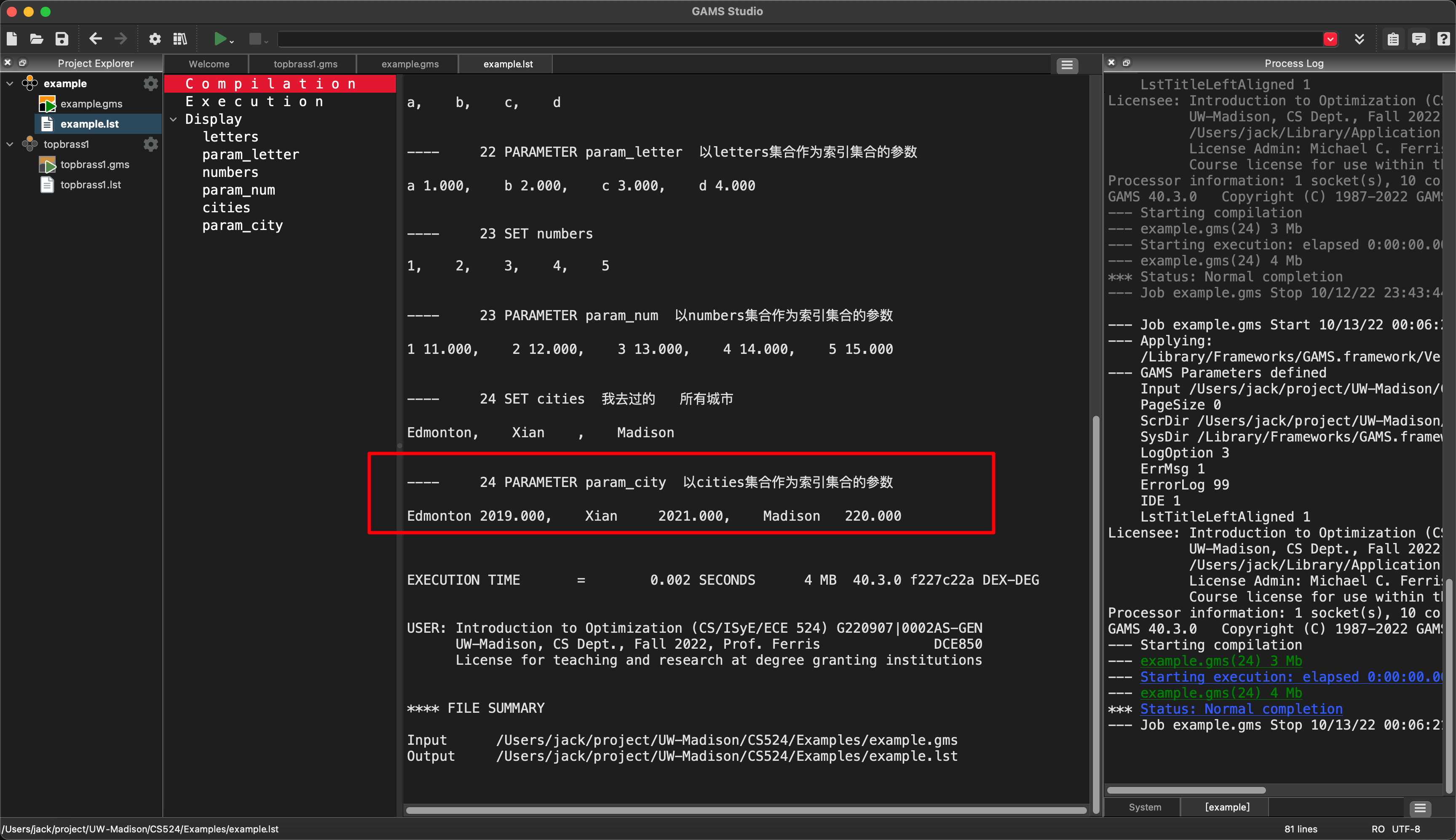
运行的结果中，可以发现Madison的值已经成了2022

参数的取值

参数的取值语法其实和参数的赋值语法没什么两样

param_name("element")

结合上面的例子，我们把param_num('1')的值赋给param_city('Madison')

Set letters /a, b, c, d/;

Sets numbers /1, 2, 3, 4, 5/,
     cities "我去过的   所有城市"
            / Edmonton  "2019去的埃德蒙顿", Xian  "2021年在西安读大学", Madison  "2022年在麦迪逊交换"/;


Parameters
    param_letter(letters)   "以letters集合作为索引集合的参数"
        / a    1, b    2, c    3, d    4 /,

    param_num(numbers)      "以numbers集合作为索引集合的参数"
        / 1 = 11, 2 = 12, 3 = 13, 4 = 14, 5 = 15 /,

    param_city(cities)      "以cities集合作为索引集合的参数"
        / Edmonton   2019, Xian = 2021/;


param_city('Madison') = param_num('1') * 20;


display letters, param_letter;
display numbers, param_num;
display cities, param_city;

运行之后的结果为

C. 表格（Table）

表格其实就是多维数组（一般都用作二维数组），因此和参数相比，表格在声明的时候需要两个集合作为索引集合，而在取值、索引的时候需要两个索引。

和参数一样下面将按照表格的声明、赋值和取值来介绍

表格的声明

GAMS中表格声明的语法如下

table table_name[(index_list)]  [text] [EOL
                element               { element }     EOL
  element    numerical_value       { numerical_value} EOL
 {element    numerical_value       { numerical_value} EOL}] ;

其中：

• []是可选项，text是注释，{}表示可重复项
• element必须是来自于索引集合中的元素
• neumerical_value必须是可解释的数值
• EOL表示回车换行

一个表格声明的例子如下

Sets
    r_idx   "行索引"    /r1 * r4/,
    c_idx   "列索引"    /a * e/;


Table t_example(r_idx, c_idx)       "一个Table Example"
        a       b       c       d       e
r1      0       1       2       3       4
r2      5       6       7       8       
r3      10      11      12      13      14
r4              16      17      18      19
;



display r_idx, c_idx;
display t_example;

需要注意的是：

• 我们在声明参数的时候，可以使用*来进行省略声明，只需要元素内是有序的即可
• 赋值是按照分隔符来给的，具体效果可以看下面的运行结果

运行结果如下，

表格的赋值与取值

表格的赋值与取值其实和参数一样的，语法为

table_name('element1', 'element2') = table_name('element3', 'element4')

下面给出一个表格赋值与取值的例子

Sets
    r_idx   "行索引"    /r1 * r4/,
    c_idx   "列索引"    /a * e/;


Table t_example(r_idx, c_idx)       "一个Table Example"
        a       b       c       d       e
r1      0       1       2       3       4
r2      5       6       7       8       
r3      10      11      12      13      14
r4              16      17      18      19
;


t_example('r4', 'a') = -2;
t_example('r2', 'e') = t_example('r2', 'c');

display r_idx, c_idx;
display t_example;

运行结果如下

D. 标量（Scalar）

GAMS中的标量就相当于C语言中的符号常量，非常简单。

标量的声明

Scalar的声明如下

scalar[s] scalar_name [text] [/numerical_value/]
       {  scalar_name [text] [/numerical_value/]} ;

其中：

• []表示可选项，text表示注释，{}表示可重复项
• neumerical_value表示可解释的数值，可以是整数或浮点数

标量声明的一个例子为

Sets
    idx   "索引"    /i1 * i4/;


Scalar
    day     "今天是这个月的第几天"      / 13 /;


display idx;
display day;

标量的赋值与取值

标量的赋值与取值非常简单，如下

Sets
    idx   "索引"    /i1 * i4/;


Scalars
    day         "今天是这个月的第几天"      / 13 /,
    day_copy    "天数的一个备份";

day_copy = day;


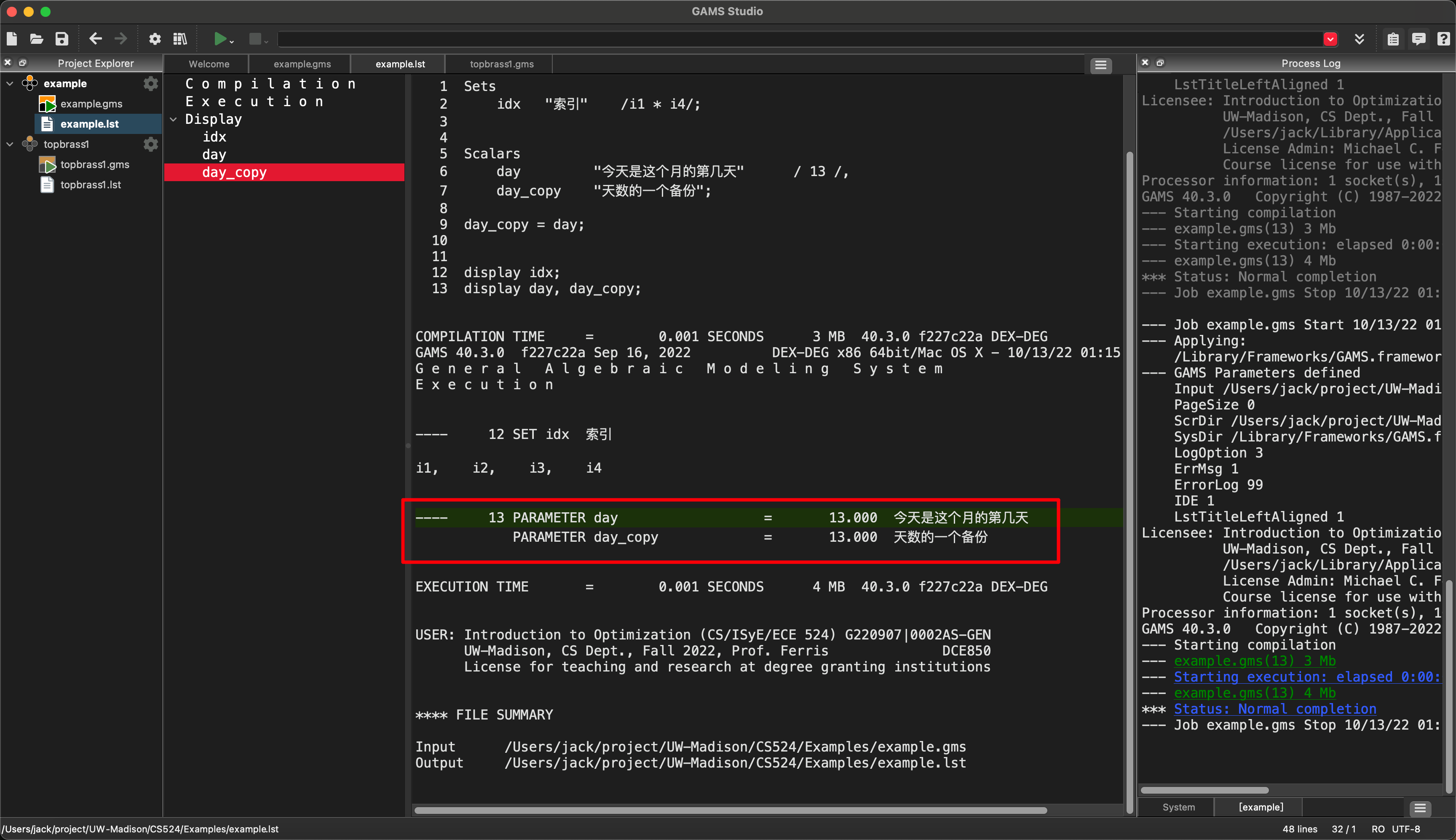
display idx;
display day, day_copy;

E. 向量化操作

Python中的Numpy包中提供了向量化操作以及广播机制，类似的，GAMS中也支持向量化操作，但是需要注意的是，GAMS不支持广播。

所谓向量化操作，意思就是逐元素操作。

向量化操作的例子如下

Sets
    r_idx   "行索引"    /r1 * r4/,
    c_idx   "列索引"    /a * e/;

Parameters
    p0(r_idx)   "待向量化操作以逐元素赋值的参数",
    p1(r_idx)   "第一个参数"    / "r1"   -1, "r2"   -2, "r3"    -3, "r4"    -4/,
    p2(c_idx)   "第二个参数"    / "a"    10, "b"    20, "c"     30, "d"     40, "e"     50/;


Table t_example(r_idx, c_idx)       "待向量化逐元素赋值的列表"
        a       c       d       e
r1      0       2       3       4
r3      10      12      13      14
r4      21      17      18      19
;

* 参数与参数的逐元素赋值
p0(r_idx) = p1(r_idx) * 10;

* 列表和参数的逐元素赋值
t_example(r_idx, 'b') = p1(r_idx);
t_example('r2', c_idx) = p2(c_idx);



display r_idx, c_idx;
display p0;
display p1, p2;
display t_example;

需要注意的是：

• 向量化操作的时候需要指明逐元素逐的是哪个索引集合
• *表示这一行为注释

运行的结果如下

2. GAMS中的变量（Variable）

通常我们的优化模型有下面几个部分组成：

• 目标变量
• 决策变量
• 约束（等式约束、不等式约束）

在约束和目标变量中，我们会有许多的参数，因此在GAMS中，使用上面介绍的Scalar、Parameter和Table三类数据类型来存储模型中的参数。

模型中的参数往往是已知值，而决策变量就是我们要求解的未知值，例如前面介绍的Top Brass Company的例子中的生产足球和橄榄球的个数。

因此，在本质上变量（Variable）是一类不同的数据类型，相比于普通的参数，会有额外的特殊属性，因此要额外介绍。

A. 变量的声明

所谓变量，值得其实就是值不知道的量，具体可以是值不知道的Scalar、值不知道的Parameter、值不知道的Table（一般多是Scalar和Parameter）。

因此变量的声明其实和前面说的三种数据类型的声明差不多的。

具体来说，变量声明的语法如下

[var_type] variable[s] var_name [(index_list)] [text] [/var_data/] {, var_name [(index_list)] [text] [/var_data/]}

其中：

• []表示可选项，text表示注释，{}表示可重复项
• var_type表示变量的类型，可以是free、positive等等，反正具体的含义就是表示了变量的取值范围。var_type所有可能的取值如下

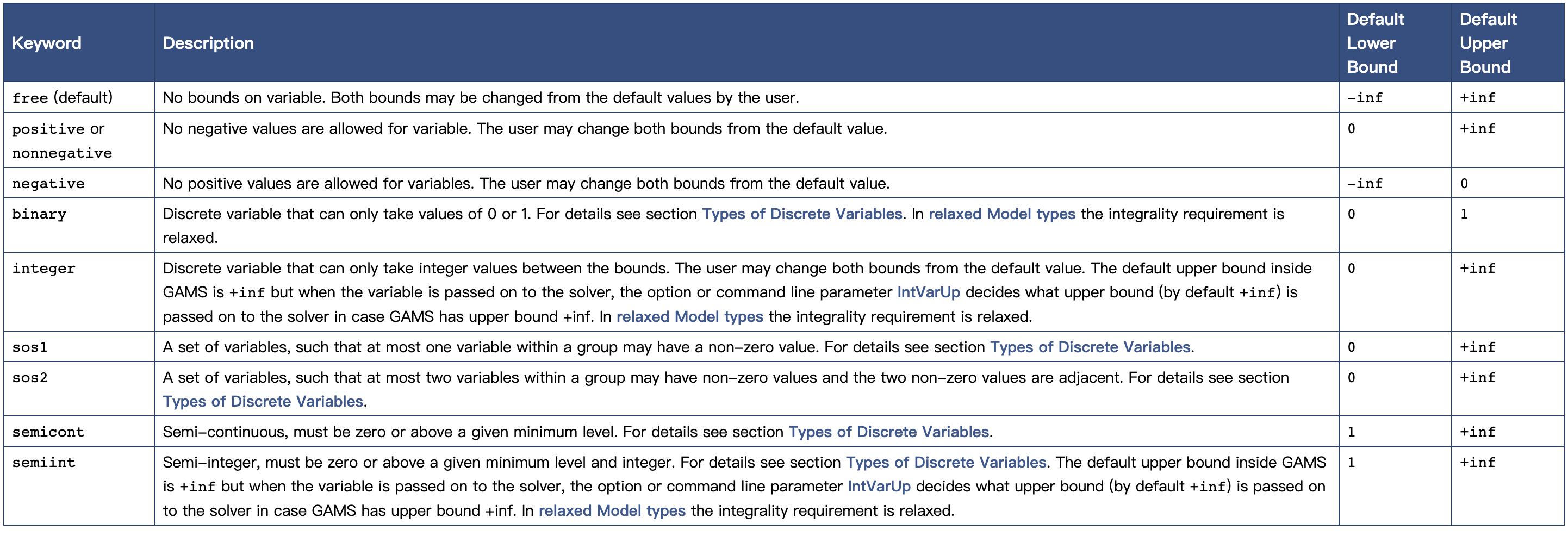
下面给出一个变量声明的例子。

注意：

• 在下面的例子中，我们声明了一个标量类型的变量和一个参数类型的变量
• 我们使用了变量的.l属性，变量的属性将在下面介绍，在这里.l属性表示变量的值

Sets
    m           "月份"                    / m1 * m4/;

Scalar
    today         "今天是这个月的第几天"      / 13 /;

Parameter
    month_sale(m)  "每个月的销售额"           / 'm1'    1, 'm2'    2, 'm3'    3, 'm4'    4/;

Variables
    what_day    "今天是第几天?",
    month_earn(m)  "每个月的利润";



what_day.l = today;
month_earn.l(m) = month_sale(m) * 20;


display what_day.l, month_earn.l;

运行的结果如下

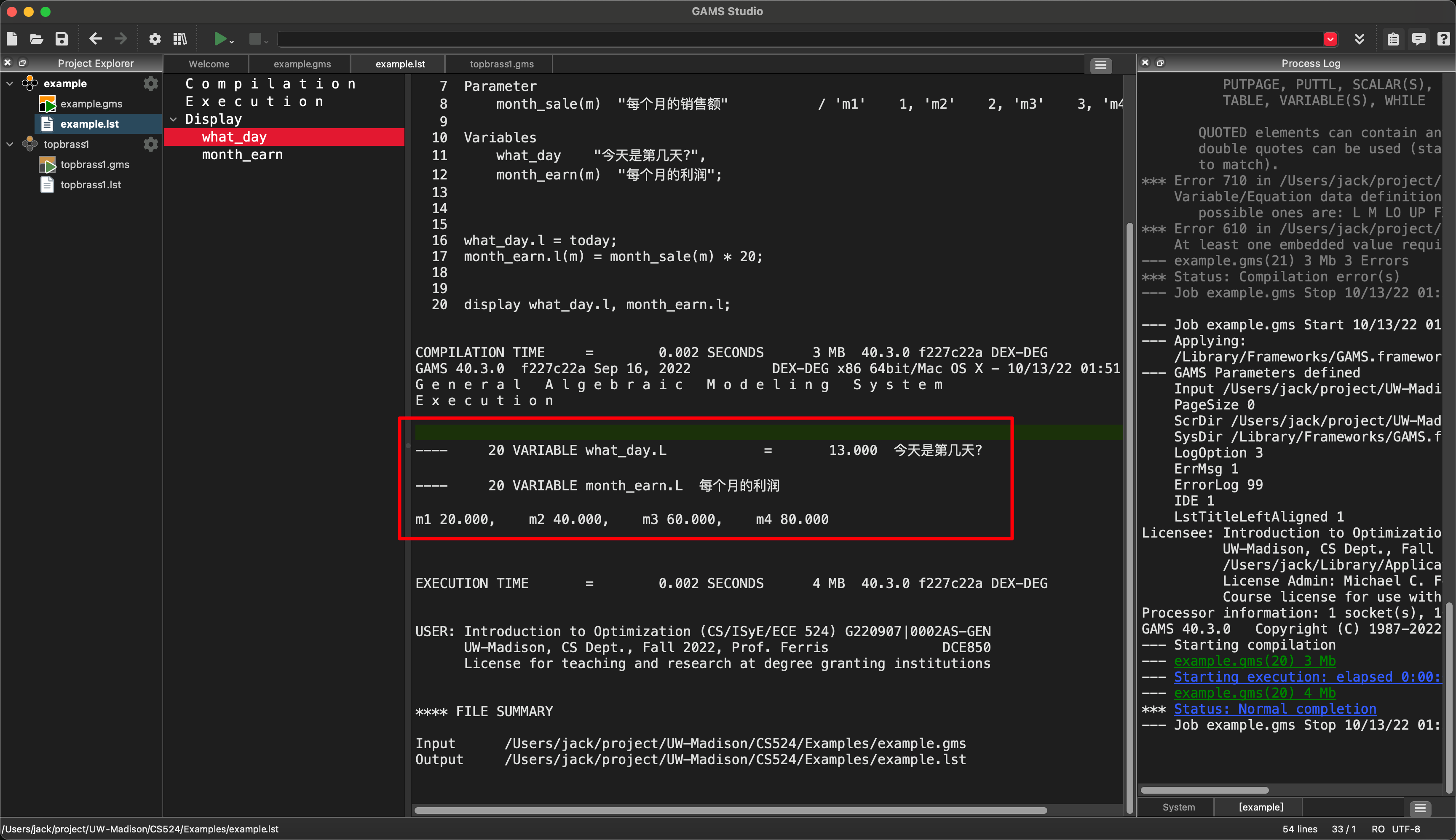
B. 变量的属性

每一个变量都有多个属性，例如上限、下限、变量的值等等。我们可以通过特殊的后缀来访问这些属性。

具体来说，所有的属性如下表所示，一般常用的就是.lo、.up和.l这三个属性

此外，需要注意的是，变量是什么了类型，对应的属性就是什么类型，例如上面的例子中month_earn(m)是参数类型的变量。

那么month_earn.l就是一个参数，我们对month_earn.l这个参数的取值和上面的参数没有任何不同。

例如下面的例子

Sets
    m           "月份"                    / m1 * m4/;

Scalar
    today         "今天是这个月的第几天"      / 13 /;

Parameter
    month_sale(m)  "每个月的销售额"           / 'm1'    1, 'm2'    2, 'm3'    3, 'm4'    4/;

Variables
    what_day    "今天是第几天?",
    month_earn(m)  "每个月的利润";



what_day.l = today;
month_earn.l(m) = month_sale(m) * 20;
month_earn.l('m3') = -100;


display what_day.l, month_earn.l;

3. GAMS程序的结构

A. 概述

GAMS程序通常包含如下的四个部分：

• 数据声明：包括Set、Scalar、Parameter和Table的声明，这里把Variable的声明也包含在内了
• 约束声明：声明所有模型中的所有约束（包含目标变量的计算式）
• 模型声明：声明某个模型包含的约束
• 求解声明：声明求解某个模型使用哪个求解器

我们前面介绍了数据声明，下面节将介绍如何声明约束、模型和求解。

B. 约束声明

约束包含两种：

• 等式约束
• 不等式约束

此外，GAMS中把目标变量的计算也视为约束。

约束的声明分为两步：

• 第一步：声明约束名称
• 第二步：定义约束计算

声明约束名称

约束名称的声明规则如下

Equation[s] eqn_name [(index_list)] [explanatory text] [/eqn_data/] {, eqn_name [(index_list)] [explanatory text] [/eqn_data/]} ;

其中：

• []表示可选项，text表示注释，{}表示可重复项

声明约束的例子如下：

Sets
  sl                      'supply locations'               /s1, s2/
  wh                      'warehouse locations'            /a, b, c/;

Equations
  tcost_eq                'total cost accounting equation'
  supply_eq(sl)           'limit on supply available at supply location'
  capacity_eq(wh)         'warehouse capacity'  /a.scale 50, a.l 10, b.m 20/;

这里需要注意的是，理论上来说，一个约束就是一个等式，那为什么约束supply_eq和capacity_eq还和sl、wh这样的索引集合关联起来呢？

原因是这样的：

我们考虑一个真实的优化问题

$$max_{x_1, x_2}\ 12 x_1 + 8 x_2\\ \left\{ \begin{array}{**lr**} mx_1 &+& nx_2 &= &z\\ ox_2 &+& px_2 &\leq &q\\ a_{11} x_1 &+& a_{12} x_2 &\leq &b_1\\ a_{21} x_1 &+& a_{22} x_2 &\leq &b_2\\ \end{array} \right.$$

那么上面这个这个优化问题用矩阵来描述实际上可以写成下面的样子

$$max_{x_1, x_2}\ 12 x_1 + 8 x_2\\ \left\{ \begin{array}{**lr**} mx_1 &+& nx_2 &= &z\\ ox_2 &+& px_2 &\leq &q\\ \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix} &\cdot& \begin{bmatrix} x_1\\ x_2 \end{bmatrix} &\leq& \begin{bmatrix} b_1\\ b_2 \end{bmatrix} \end{array} \right.$$

那么上面的约束实际上只有三个，其中：

• 第一个约束是一个标量等式约束
• 第二个约束是一个标量不等式约束
• 第三个约束是一个矩阵不等式约束

但是第三个约束实际上是对$x_1$和$x_2$和两个变量的约束，因此我们在GAMS中声明矩阵约束的时候，实际上就需要和索引集合关联起来。

定义约束计算

约束计算的式子如下

eqn_name(index_list)[$logical_condition(s)].. expression eqn_type expression ;

其中：

• []是可选项
• eqn_type是约束的类型，expression就是加减乘除的表达式
• $logical_condition是逻辑表达式，我们在下一讲中将涵盖这个主题

所有的eqn_type有

定义约束计算的一个例子如下

Variables  phi, phipsi, philam, phipi, phieps ;
Equations  obj ;

obj.. 
    phi  =e=  phipsi + philam + phipi - phieps ;

标量约束

我们在上面介绍了标量约束和矩阵约束，下面将给出下面这个约束问题代码

$$max_{x_1, x_2}\ 12 x_1 + 8 x_2\\ \left\{ \begin{array}{**lr**} mx_1 &+& nx_2 &= &z\\ ox_2 &+& px_2 &\leq &q\\ \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix} &\cdot& \begin{bmatrix} x_1\\ x_2 \end{bmatrix} &\leq& \begin{bmatrix} b_1\\ b_2 \end{bmatrix} \end{array} \right.$$

首先是标量约束的定义和声明

$$\left\{ \begin{array}{**lr**} mx_1 &+& nx_2 &= &z\\ ox_2 &+& px_2 &\leq &q\\ \end{array} \right.$$

Scalars
    m  /1/,
    n  /2/,
    z  /3/,
    o  /4/,
    p  /5/,
    q  /6/;

Set
    position        "位置索引"            /1, 2/;

Parameters
    eq1_p(position)                "第一个等式约束的参数"      /    "1"    1, "2"   2 /,
    eq2_p(position)                "第二个不等式约束的参数"  / "1"    4, "2"   5 /;



Free Variable 
    objective,
    decision(position);


Equations
    eq1,
    eq2;


eq1..
    sum(position, eq1_p(position) * decision(position)) =e= z;

eq2..
    sum(position, eq2_p(position) * decision(position)) =l= q;

矩阵约束

然后我们再定义矩阵约束

$$\left\{ \begin{array}{**lr**} \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix} &\cdot& \begin{bmatrix} x_1\\ x_2 \end{bmatrix} &\leq& \begin{bmatrix} b_1\\ b_2 \end{bmatrix} \end{array} \right.$$

注意，这里使用alias的原因是因为我们的等式应该是对每行循环的，而求和是对每个变量循环的。

Scalars
    a11 /7/,
    a12 /8/,
    a21 /9/,
    a22 /10/,
    b1  /11/,
    b2  /12/;


Set
    position        "位置索引"            /1, 2/;

alias (row, position);

Parameters
  eq3_b(row)             "第三个矩阵约束"         / "1"    11, "2"  12 /;



Table a(row, position) "系数矩阵a"
        "1"     "2"
"1"     7       8
"2"     9       10
;

Free Variable 
    objective,
    decision(position);


Equations

    eq3(row);


eq3(row)..
    sum(position, a(row, position) * decision(position)) =l= eq3_b(row);

C. 模型声明

模型声明很简单，语法如下

model[s] model_name [text] [/ (all | eqn_name {, eqn_name}) {, var_name(set_name)} /]
       {,model_name [text] [/ (all | eqn_name {, eqn_name}) {, var_name(set_name)} /]} ;

其中：

• []表示可选项，{}表示可重复项，text表示注释

语法具体来说就先声明模型的名字，然后在//中声明模型包含的约束

例如对上面的例子，我们声明的模型为

model example "示例"    /eq1, eq2, eq3/;

D. 求解声明

求解声明其实就是说明我们需要使用哪个求解器求解模型，具体语法如下

solve model_name using model_type maximizing|minimizing var_name;
solve model_name maximizing|minimizing var_name using model_type ;

其中：

• model_name就是需要求接的模型名称
• model_type就是使用的求解器的名称
• var_name就是需要最大或者最小化的目标变量

常用的求解器有：

对于上面的模型，我们的求解声明如下

Set
    position        "位置索引"            /1, 2/;

Free Variable 
    objective,
    decision(position);


Equations
    obj_eq;


obj_eq..
    objective =e= 12 * decision("1") + 8 * decision("2");


model example "示例"    /obj_eq/;

solve example using lp maximizing objective;

E. 总结

最后，我们把上面所有的内容结合起来，就完成下属优化模型的GAMS程序描述

$$max_{x_1, x_2}\ 12 x_1 + 8 x_2\\ \left\{ \begin{array}{**lr**} mx_1 &+& nx_2 &= &z\\ ox_2 &+& px_2 &\leq &q\\ \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix} &\cdot& \begin{bmatrix} x_1\\ x_2 \end{bmatrix} &\leq& \begin{bmatrix} b_1\\ b_2 \end{bmatrix} \end{array} \right.$$

GAMS程序为

Scalars
    m  /1/,
    n  /2/,
    z  /3/,
    o  /4/,
    p  /5/,
    q  /6/,
    a11 /7/,
    a12 /8/,
    a21 /9/,
    a22 /10/,
    b1  /11/,
    b2  /12/;


Set
    position        "位置索引"            /1, 2/;

alias (row, position);

Parameters
    eq1_p(position)                "第一个等式约束的参数"      /    "1"    1, "2"   2 /,
    eq2_p(position)                "第二个不等式约束的参数"  / "1"    4, "2"   5 /,
    eq3_b(row)             "第三个矩阵约束"         / "1"    11, "2"  12 /;



Table a(row, position) "系数矩阵a"
        "1"     "2"
"1"     7       8
"2"     9       10
;

Free Variable 
    objective,
    decision(position);


Equations
    eq1,
    eq2,
    eq3(row),
    obj_eq;


eq1..
    sum(position, eq1_p(position) * decision(position)) =e= z;


eq2..
    sum(position, eq2_p(position) * decision(position)) =l= q;


eq3(row)..
    sum(position, a(row, position) * decision(position)) =l= eq3_b(row);


obj_eq..
    objective =e= 12 * decision("1") + 8 * decision("2");


model example "示例"    /eq1, eq2, eq3, obj_eq/;

solve example using lp maximizing objective;

最后的结果如下，变量objective的最大值是4