
1. 前言
算法对于一个计算机系的学术来说,是最终的课程之一,也是程序员必修内功之一。而本文其实是我在学习算法设计这门课的时候NP完全性理论部分的笔记。因为我自己真心觉得我这个笔记做得不错,所以特地将NP完全性理论部分的笔记整理出来,写成博客,以飨读者。
2. NP完全性理论 —— 基础
学一个东西,需要明白它是干什么用的
NP完全性理论是一个研究问题类别的理论。和回溯法、动态规划等研究具体某一类问题的求解不同,NP完全性理论是研究问题之间关系的理论。
因此,明白这个道理之后,我们就知道,NP完全性理论其实并不是帮助我们去求解某一类问题的,而是帮助我们去认识问题的。
A. Lead-in:多项式时间问题和指数时间问题
时间复杂度有很多种,每一个问题都可以有一个求解算法,而每一个求解算法都有时间复杂度。因此我们如果用某一个问题的最优算法来表征这个问题,那么就可以说这个问题是xxxx(时间复杂度)问题。例如对于0/1背包问题,我们最好的求解算法的时间复杂度是$\mathcal{O}(2^n)$,那我们就可以称0/1背包问题为$\mathcal{O}(2^n)$问题。
那么根据时间复杂度来进行划分,我们就可以把问题分成两大类:多项式时间问题(Polynomial Time Problem)和指数时间问题(Exponential Time Problem)。
后文中会把中文的
多项式时间问题和指数时间问题与英文简称Polynomial和Exponential混用。
常见的多项式时间问题和指数时间问题有:
| 多项式时间问题 | 多项式时间问题 | 指数时间问题 | 指数时间问题 |
|---|---|---|---|
| 算法名称 | 时间复杂度 | 算法名称 | 时间复杂度 |
| Linear Search | $\mathcal{O}(n)$ | 0/1 Knapsack | $\mathcal{O}(2^n)$ |
| Binary Search | $\mathcal{O}(\log n)$ | Traveling SP | $\mathcal{O}(2^n)$ |
| Intersection Sort | $\mathcal{O}(n^2)$ | Sum of Subset | $\mathcal{O}(2^n)$ |
| Merge Sort | $\mathcal{O}(n\log n)$ | Graph Coloring | $\mathcal{O}(2^n)$ |
| Matrix Manipulation | $\mathcal{O}(n^3)$ | Hamilton Cycle | $\mathcal{O}(2^n)$ |
那还有一个问题就是,为什么要分为多项式时间问题和指数时间问题呢?其实是因为这两类问题本质上存在不同,多项时间的问题是简单问题/易问题,而指数时间是难问题。类比人类做数学题的样子,如果我们求解一个问题花的时间非常长,那么这个问题就非常难。如果花的时间短,那么这个问题就是一个简单问题。
例如,假设某个问题A的最优算法时间复杂度是$\mathcal{O}(n^{100})$,问题B的最优算法的时间复杂度是$\mathcal{O}(2^n)$,那么虽然一开始问题规模比较小的时候是问题A更难,但是当问题规模一定大了之后,即$n$一定大了之后,问题B更难。因此,最终/从根本上来说,问题B更难。
所以我们才说,多项式时间问题是简单问题,而指数时间问题是难问题。
B. NP完全性理论的idea
NP完全性理论起源于两个idea:
- 能否为所有的Exponential的问题进行分类?更详细的说,目前有很多问题已知的最好的求解算法是Exponential Time的,那么对于这些问题,他们之间是否存在相似性?进一步,我们能否利用这种相似性来对所有的Exponential Time的问题进行划分,这样的话对于划分后的每一组问题,只需要解决组内的一个问题,然后稍加变形就可以解决这一组的所有问题。
- 如果不能为一个目前最好的算法是Exponential Time的问题写出Deterministic的Polynomial Solution,那么能否为其写出一个Non-Deterministic的Polynomial Solution?
而整个NP完全性理论,就是从这两个idea中发展出来的。从这两个idea出发,就可以构建出整个NP完全性理论
C. 确定性算法(Deterministic)与非确定性算法(Non-Deterministic)
上面我们在说NP完全性理论的时候说到了确定性算法和非确定性算法,那么这两个术语的意思是什么呢?
确定性算法
所谓确定性算法,指的就是由确定性的算法语句组成的算法。而所谓确定性语句,指的就是我们明白其内部流程(对于函数)的语句。
简单的理解确定性算法,就是我们知道这个算法的实现,写不住来只是因为单纯的码力问题。
举一个确定性算法的例子,下面这个算法是利用OrbSLAM2算法对周围环境建立三维地图的程序。
// 需要opencv
#include <opencv2/opencv.hpp>
// ORB-SLAM的系统接口
#include "System.h"
#include <string>
#include <chrono> // for time stamp
#include <iostream>
using namespace std;
string parameterFile = "./myvideo.yaml";
string vocFile = "./Vocabulary/ORBvoc.txt";
string videoFile = "./myvideo.mp4";
int main(int argc, char **argv) {
// 声明 ORB-SLAM2 系统
ORB_SLAM2::System SLAM(vocFile, parameterFile, ORB_SLAM2::System::MONOCULAR, true);
// 获取视频图像
cv::VideoCapture cap(videoFile); // change to 1 if you want to use USB camera.
// 记录系统时间
auto start = chrono::system_clock::now();
while (1) {
cv::Mat frame;
cap >> frame; // 读取相机数据
if ( frame.data == nullptr )
break;
// rescale because image is too large
cv::Mat frame_resized;
cv::resize(frame, frame_resized, cv::Size(640,360));
auto now = chrono::system_clock::now();
auto timestamp = chrono::duration_cast<chrono::milliseconds>(now - start);
SLAM.TrackMonocular(frame_resized, double(timestamp.count())/1000.0);
cv::waitKey(30);
}
SLAM.Shutdown();
return 0;
}
虽然我不知道OrbSLAM2算法的底层实现,即我们不知道诸如SLAM.TrackMonocular()、chrono::system_clock::now()等函数/方法的内部是怎么写的,但是OrbSLAM2算法的原理我们(人类)是知道的,只要我们花时间去学习,假以时日我们就能自己写出来。
非确定性算法
既然确定性算法是我们知道原理的算法,那么非确定算法就是我们不知道原理的算法,而不是我们没有学习原理的算法。我们没有学习原理的算法,他的原理已经被人发现了,就放在那里,是你不学。而非确定性算法,其原理还没有人发现过,目前还是未知。
所以,我们之前写的所有的程序、实现的所有算法,都是确定性算法。那么问题就来了,我们不知道确定性算法,那么到底该怎么写出来非确定性算法?
很简单,把非确定性算法中我们不会写的、并且是Polynomial的地方留白,未来当我们知道这个地方怎么写了,我们再把留白的地方补上去。
这样解释还是比较含糊不清,下面就举一个非确定性算法的例子。
N-Search问题:给定一个随机数组A,和一个值key,要求值key是否存在于数组A中。
求解这个问题最简单的算法就是遍历数组A就行了,这样的话得到的算法时间复杂度是$\mathcal{O}(n)$。而我们能够写出这样的算法,因此,下面的
n-search1算法就是确定性的算法bool n-search1(int A[], int n, int key){ for (int i = 0; i < n; i++) if (A[i] == key) retutrn true; return false; }因此,目前我们能够找到的N-Search问题最好的算法是$\mathcal{O}(n)$的,因此N-Search问题是$\mathcal{O}(n)$问题。
那么我们接下来就要问了,N-Search问题是否存在$\mathcal{O}(1)$的算法?你当然可能会想,肯定不存在这样的算法,因为要挨个比较每个元素,因为……诸如此类的原因其实都是我们人认为的。可是,在数学上,我们否定一个问题是需要给出严格的证明的。可是,对于”N-Search问题不存在$\mathcal{O}(1)$的算法“这个问题,我们在数学上没有办法给出严格的证明。
因此,我们其实没法否认”N-Search问题存在$\mathcal{O}(1)$的算法“这个命题,有可能在未来某一天,我们就真的找到了的算法。但至少在目前,我们是不知道这个算法的。为此,我们可以用下面的方式来表示
bool n-search2(int A[], int n, int key){ // choice函数是n-search的O(1)的解法 int idx = choice(); if (A[idx] == key) return true; return false; }那么这样,
n-search2算法就是n-search问题的一个$\mathcal{O}(1)$的算法,只不过其中的操作我们并不知道原理,即choice语句到底是怎么样用$\mathcal{O}(1)$来找到一个idx的?这就是为什么我们说
n-search2算法是non-deterministic的。而对于choice语句来说:When we don't know how it works, it's magic. Once we know it, it's technique.
至此,我想上面的这个例子已经很清楚的解释了,什么是非确定性的算法。
而对于所有的非确定性算法,可能我们今天不知道非确定性算法是怎么工作的,但是可能我们明天就知道的了,那么明天这个非确定性算法就变成了确定性算法了。
为什么要用非确定算法?
我们上面介绍了确定性算法和非确定性算法,那么我们就想要问,确定性算法我们可以写出来,因此确定性算法是有其实际意义的。可是,非确定性算法我们根本没法写出来,他到底有什么用呢?
哈哈,别忘了我在前面说过的,NP完全性理论的目的:研究问题之间的关系。非确定性算法恰恰就是用于帮助我们去研究问题之间关系的工具。
接下来,我们就要开始用确定性与非确定性算法来研究NP问题了。
D. P类问题与NP类问题
我们前面举了一个例子,例子中我们为n-search这个目前只有$\mathcal{O}(n)$的问题写出了$\mathcal{O}(1)$的非确定性算法。
那么以此类推,我们其实可以给所有的Exponential 问题写出来Polynomial的Non-Deterministic的解法。
因此,我们定义:
- 用P来表示所有具有Polynomial Time的Deterministic Solution的问题(Polynomial Problem)。
- 用NP来表示所有具有Polynomial Time的Non-Deterministic Solution的问题(Non-deterministic Polynomial Problem)。
即:
- P类问题是目前我们已经能够为其写出确定性多项式时间算法的问题
- NP类问题是目前我们只能够为其写出非确定性多项式时间算法的问题
注意,因为我们说不确定的算法可以变成确定的算法,因此NP问题如果我们找到了确定性的解法,那么这个NP问题就成为了P类问题。因此,P类问题和NP类问题有一个重要的性质,就是
到这里,我们其实已经完成了NP完全性理论的第二个问题,即我们为Polynomial Time的问题写出了Non-deterministic的Polynomial算法。
3. NP-Hard与NP-Complete问题
在介绍完了NP完全性理论的基础之后,我们接下来要介绍的,就是NP-Hard问题与NP-Complete问题,即NP难问题与NP完全问题。
A. 问题的相似性
在开始介绍NP-Hard和NP-Complete问题前,先通过一个例子,阐述问题的相似性。
CNF-Satisfactory问题/合取范式问题
CNF-Satisfactory问题/合取范式问题
写代码的时候,我们经常遇到一个很长的逻辑表达式,然后针对表达式中的各个变量,到底在取什么值的时候表达式的值为真?那么这个问题就是合取范式问题,即CNF-Satisfactory问题。
我们形式化的描述一下CNF-Satisfactory问题:给定0-1变量集合${x_1,x_2,…,x_n}$,给定范式(即逻辑表达式)$CNF=f(x_1,x_2,…,f_n)$,求$\vec x={x_1,x_2,…,x_n}$,使得
CNF成立。
举个CNF-SAT问题(CNF-Satisfactory简写为CNF-SAT)的例子:
设$\vec x = {x_1,x_2,x_3}$,求$\vec x_0$,使得$CNF=(x_1\or\bar x_2 \or x_3) \and (\bar x_1 \or x_2 \or \bar x_3)$成立(为真)。
求解这个问题,我们当然可以用遍历的方法去做,这样的话我们需要遍历八种可能。
| $x_1$ | $x_2$ | $x_3$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
但其实,我们可以把解空间组织成一个树的形式,而后利用分支限界或者回溯法来高效的遍历。

0/1背包问题
对于0/1背包问题的介绍,建议查阅知乎文章:https://zhuanlan.zhihu.com/p/30959069,这里就不再啰嗦了。
问题相似性
对于0/1背包问题,我们对于每一个物品,可以用一个布尔变量$x_i$来表示拿或者不拿这个物品。那么这样的话,我们其实也可以把0/1背包问题,用一个树来表示。
那么,如果现在我们拿到了一个展开树/解空间树,我们其实是不知道这个树是01背包问题还是CNF-Satisfactory问题,这是因为,在本质上,01背包问题与CNF-Satisfactory问题是一类问题,都可以用解空间树来表示,而且,这两个利用解空间树进行求解的方法也是一样的
由此可见,诸多的问题之间,其实是存在相似性的,我们可以利用这一相似性,对问题进行划分。那么问题的关键,就在于现在假设有两个问题A和B,我们要如何得知这两个问题是否是同一类问题呢?
问题规约
上面我们通过0/1背包问题和CNF-SAT问题的这个例子,说明了问题之间存在相似性。那么现在给定两个问题,如何判断这两个问题之间是否有相似性呢?
具体的判断方法,就是看两个问题能否规约到一起去。即问题A能否规约到问题B,或者问题B能否规约到问题A。而规约的含义,就是对一个问题进行一定的变换,例如我们上面对0/1背包问题进行了变换,变换到了解空间树上去。而这一变换,术语称为规约,问题$L_1$可以归约到问题$L_2$记为:$L_1\propto L_2$。
注意,规约要求进行问题变换的时候,花费的时间也必须是多项式时间的,并且进行变换的算法必须是已知的,因为我们必须知道这个变换的方式,否是没有办法把问题B变换到问题A上去的。其次如果不存在多项式时间的变换,那么这个变换也是没有意义的,因为变换所花费的时间不必直接求解问题B要多。
规约的一个好处就是,如果我们用变换$f$将问题A变换为了问题B,那么我们对B问题的解法进行逆变换$f^{-1}$,就可以得到问题A的解法。
因此规约带来的的好处就是我们可以通过研究同一类问题中的其他比较容易解决的问题,来解决不好解决的问题。例如上面用合取范式求解背包问题。
更进一步,对于同一类问题我们其实只需要求解其中的一个就行了,剩下的就是寻找待解决的问题和已经解决的问题之间的变换$f$,找到了之后利用逆变换就可以求出来待解决问题的解。而变换$f$其实很好求,通常都是只需要做到解空间对应即可。
B. NP-Hard问题
我们接下来定义一类特殊的问题,定义:CNF-SAT问题是一个NP-Hard问题。设问题$L$,若$L\propto CNF-SAT$,则$L\in NP-hard$,即所有可以归约到$CNF-SAT$的问题都是NP-hard问题。注意,我们并没有说不能规约到$CNF-SAT$的问题就不是NP-hard问题
首先我们需要明白,NP-hard问题和NP问题有什么关系。NP问题的定义就是能够写出Polynomial Time的Non-Deterministic解法的问题。但是NP-hard问题中只有一部分能否写出来Polynomial Time的Non-Deterministic解法,因此$NP-hard\subset NP$不成立,只能是$NP-hard\cap NP\neq \varnothing$。
NP-hard问题的定义可能一开始看会觉得很奇怪,感觉这样一个“问题+规约”的形式的定义有些怪怪的。
其实一点都不怪,还记得前面说过的NP完全性理论的目的么?NP完全性理论就是研究问题之间的相关性的,所以先定义一个问题作为”根问题“,而后用归约作为桥梁,来扩充NP-hard类问题的集合。
之所以要定义出来NP-hard类问题,是为了和接下来的NP-Complete问题比较。
C. NP-Complete问题
定义:若一个问题存在Polynomial Time的Deterministic解,那么该问题就是NP-Complete问题
同样的,NPC问题也可以通过规约来进行传递,即:设问题$L_1\in NP-Complete$,若问题$L_2\propto L_1$,则$L_2\in NP-Complete$。
我们再给出一个定理:$SAT\in NP-Complete$。这个定理的证明书上有7页,我就不放了。反正就是说明了SAT是一个NPC问题。
4. P=NP?
前面说了一大堆,介绍了P类问题,NP类问题,NP-hard类问题,NP-Complete类问题,我们画个图来表示一下他们之间的关系:
- $P\subset NP$
- $NP-hard\cap NP\neq \varnothing$
- $SAT\in NPC$,且$SAT\in NP-hard$,故$SAT\in NPC$
- $\forall L,\ if\ L\propto SAT,\ then\ L\in NP-hard\ and\ L\in NP-Complete\ and\ L \in NP$,故$NPC=NP-hard\cap NP$
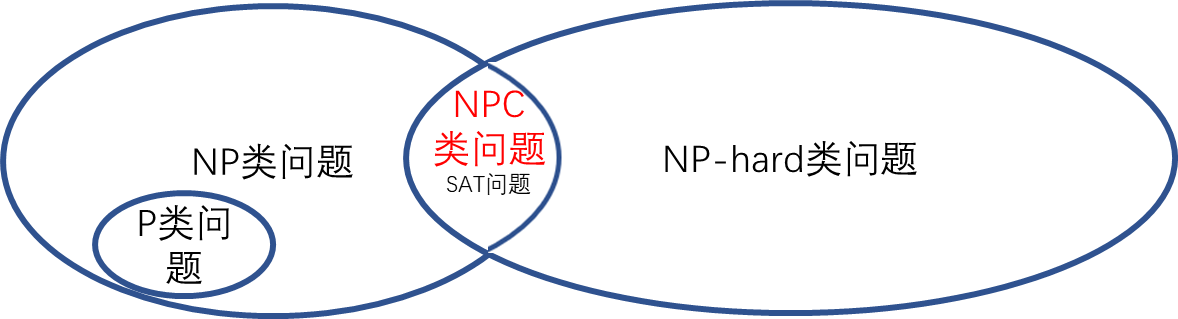
那么最后,我们还有一个问题,就是随着我们发现越来越多的算法,P类问题变得越来越大,那么有一天,P类问题会不会变得和NP类问题一样大?即会不会有一天,我们为所有的NP问题找到了确定性的多项式时间算法呢?用数学语言表示,$P=NP$还是$P\neq NP$?这个问题就是著名的$P-NP$问题
如果$P=NP$,那么就说明当前所有指数时间的算法都是存在多项式时间的解法的,只不过我们还没有发现它。
$P=NP$会带来很大的影响。例如,目前绝大多数的加密算法经过精心的设计,使得破解加密的算法的时间复杂度是次数非常夸张的多项式时间,例如$\mathcal{O}(1000000^n)$,这样,我们加密后的密码是256位的,那么破解密码需要的计算时间为$\mathcal{O}(1000000^{256})$,这个让计算机一直计算完一个人的一生也算不到,因此就不可能破解出来我们的密码。
可是如果$P=NP$,那么就意味着其实存在多项式时间的算法来破解密码,只不过我们现在还没有找到。
所以说,如果$P=NP$,那么对于所有的算法来说,就有:
We are not inventing it, we are discovering it.
5. 后记
A. NP-Complete问题树
我们前面说,规约$\propto$可以传递问题的NPC、NPH等性质,所以基于$SAT$这个基问题,人们不断地将一些问题归约到了SAT问题上去,从而我们就为NP完全问题构建出来了一个NP完全问题树。

B. P-NP问题的研究进展
最后,目前关于$P=NP$问题的研究的进展,最大的一个就是著名的Cook定理,Cook定理说的是个什么事呢?
Cook定理是说:$P=NP\Leftrightarrow SAT\in P$
即如果我们能够为SAT问题找到一个多项式时间的解,那么$P=NP$。因此,基于Cook定理,现在大家在做的事情就是想办法证明$SAT\in P$
但是由于直接为$SAT$问题找到多项式时间的解实在是太难了,所以人们就利用上面的NPC问题树,只要解决了这个树中的任何一个问题$L$,那么由于规约的定义中规约时进行变换花费的时间也必须是多项式时间的,因此我们再花费多项式的时间将其解法归约到$SAT$问题山去,那么我们就完成了$N-NP$问题的证明。



