本文是XJTU计算机视觉2022 Spring 第三节课的笔记，本节课主要讲解了人的视觉系统、摄像机的结构以及摄像机的模型。

XJTU计算机视觉2022-Spring-3: 成像原理与相机模型

我们上节课讲解了数字图像的基础知识，包括图像这种数据在计算机中的表示、数字图像的基本属性……本节课将讲解获得图像的设备/器官，即人眼之于人体，摄像机之于计算机。

抽象的来说，他们都是收集光的机器。因此本节课就将具体的讲解他们。

具体来说，本节课包含以下内容

不过由于我所写的是笔记，而非课程的PPT的复制粘贴，因此我将有选择性的介绍一些内容。

1. 人的视觉系统

对于人来说，人有五种感觉。这五种感觉其实是人对真实世界中五种物理量的表示。

为了要获得这五种感觉，人就需要分别有五个感知系统来分别感知这些物理量。视觉（光信号）信息就是由人的视觉系统收集的。

下面将详细的对人的视觉系统进行介绍。

1.1 人眼的结构

人眼的结构如下所示：

• 首先当物体发出的、折射的光会经过晶状体和角膜，从而被折射。然后通过小孔完成小孔成像的这一个过程。
• 人的视网膜上存在很多可以感知不同种颜色的光的神经细胞，因此最终当外界的物体的光经过人眼的结构最终打在视网膜上之后，我们就会感受到这些光。
• 我们的大脑进一步会对这些光进行处理，最终组合、形成我们看到的物体。

1.2 人眼各结构的功能

总结来说，人眼各个结构的功能如下

1.3 人眼感知的光的范围

光本身是波，而人眼所能够感受到的光也是有范围的。一般是从380到760纳米

1.4 人眼感知光的原理

上面说到，人眼最终感知光是依靠视网膜的，那么具体来说视网膜是如何感知光的呢？因为光只是光信号，而大脑能够处理的是电信号。所以人眼中就一定存在这把光信号转换为电信号的结构。

其实完成转换的这个结构就是视网膜，更具体的来说，是视网膜上的两种四类细胞。

视网膜上这些细胞分别是：

• 视杆细胞（Rod Cell）
• 视锥细胞（Cone cell）
  • S-Cone
  • M-Cone
  • L-Cone

不同的细胞负责对不同的光信号产生反应。视杆细胞主要对光的明暗变化（总光强）有反应，而视锥细胞则是对不同种光的明暗变化（某种颜色光的光强）有反应。

视锥细胞可以分成三类，分别是S、M、L，这三类细胞分别对蓝色、绿色、红色的光有反应

因此，视网膜的详细结构如下：在诸多的视杆细胞中夹杂着视锥细胞

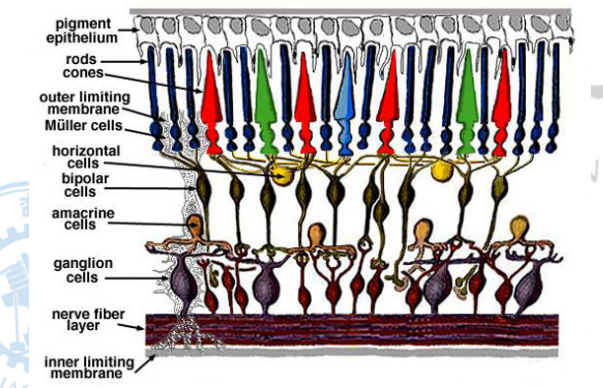
1.5 视觉的时间域响应特性

最后，人眼其实是有一个时间响应特性的

最后，总的来说，人眼是一个收集光的机器

2. 相机的结构

我们上面介绍了人的视觉系统，其中很多的笔墨花在了介绍人眼的结构上。我们现在想要让机器去收集光、形成图像，那么我们就需要让机器去模拟人的眼睛。

因此下面就将详细介绍一下相机的结构

2.1 小孔成像

现在我们如果直接在需要拍摄的物体前放置一个相机的话，那么最终其实是没有办法获得这个物体的图像的。

因为对于胶片上的某一点来说，它感受到的光是包含了来自于这个物体各个地方的光，所以rather than巴黎铁塔的像，胶片上的图像是铁塔的average的图像。

为此，我们其实就需要使用小孔成像，换而言之只让一部分光通过

2.2 小孔相机模型

上面说道，我们的相机为了最后能够形成一个像，就需要使用小孔成像原理。那么对应的，这种相机模型就就称为小孔相机模型。对应的，有一些小孔相机模型的术语

2.3 光电转换

在成功的捕获到了现实世界中物体的光之后，类比于人类的眼睛，接下来的一步就是完成从光到电信号的转换。

为了完成这个转换，我们可以使用半导体元件CMOS。我们这里不去深究CMOS元件具体是如何完成光电转换的，我们这里只需要知道半导体元件可以完成光电转换即可。

所以，数码相机就是在成像平面上放置一个CMOS的阵列。这个阵列就可以完成从光到电信号的转换。

不同的CMOS元件可以捕获不同的类型的光，即可以把不同颜色的光转换为电信号。所以，我们可以类似于人的视网膜一样，在成像平面上放置捕获三种光的CMOS，从而实现捕获彩色图像

3. 相机模型

上面我们介绍了相机的结构和成像原理，下面我们将介绍相机模型。所谓的相机模型，其市指的就是在建立空间坐标系之后，空间中一点到相机图像上一点的变换

3.1 从三维空间到成像平面的变换

我们下面先完成三维空间中一个点到相机成像平面的变换。

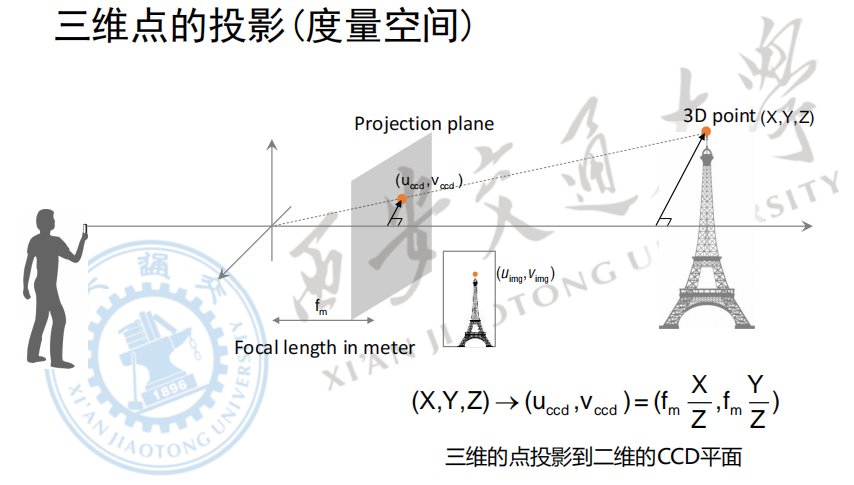
我们把三维空间中的一个点的坐标记为：$(X,Y,Z)$，记该点在成像平面上对应的点的坐标为：$(-u{ccd},-v{ccd})$

那么根据相似三角形，就有

$$(X,Y,Z)\rightarrow (u_{ccd}, v_{ccd})=(f_m\frac X Z, f_m\frac Y Z)$$

上式中，$X,Y,Z$、$u{ccd},v{ccd}$和$f_m$都是以米为单位的

为了方便后面的推导，我们把左边的CMOS平面对称到右边来，如下图

3.2 从成像平面到像素坐标

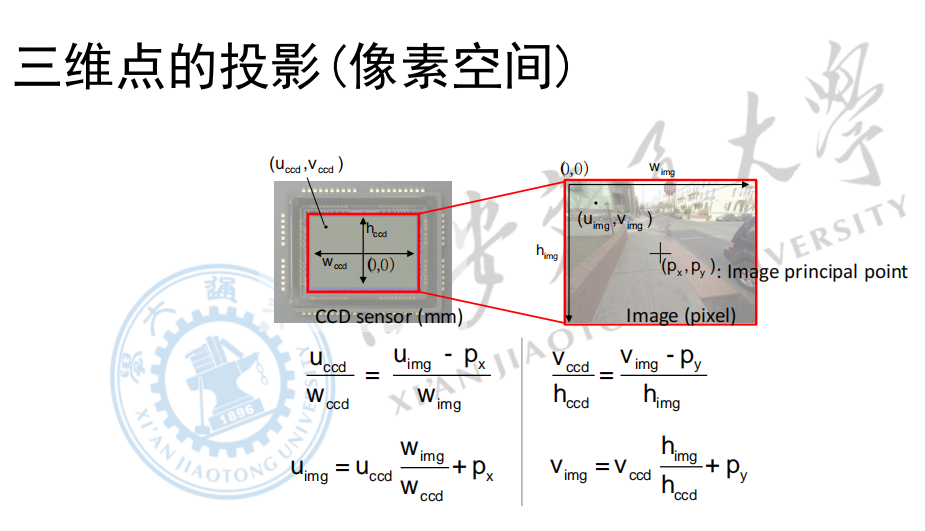
我们接下来需要完成的，就是从CMOS阵列上的物理坐标转换到图像的像素坐标上去。

对于成像平面，一般以中心点为原点，建立直角坐标系。而对于像素坐标，一般以左上角为原点，建立直角坐标系。

成像平面的坐标系中左上角为正，像素坐标中右下为正。

同样，我们由相似三角形可以知道，虽然像素坐标和成像平面坐标的单位不同，但是自己除以自己就把单位化掉了。

3.3 三维空间到像素平面

接下来，我们结合上面两步，完成从三维空间到像素平面的投影。我们直接把$u{ccd}$和$v{cdd}$的计算式直接带入即可

因为$fm$、$w{img}$、$w{ccd}$、$h{img}$、$h_{ccd}$等值其实都是固定的值，在相机出厂的时候就已经确定了（虽然现在有变焦相机，但是变焦相机的焦距使我们手动调整的，所以我们其实是知道这个焦距的，而CMOS的长、宽，拍摄图像的分辨率都是固定的）。因此我们其实可以吧上面两个绿框内的值用一个固定的值来表示。

下式中，$f_X$和$f_Y$分别表示以像素计量的焦距。即焦距等于多少个像素，像素的物理宽度米则是由相机本身决定。

3.4 三维透视变换

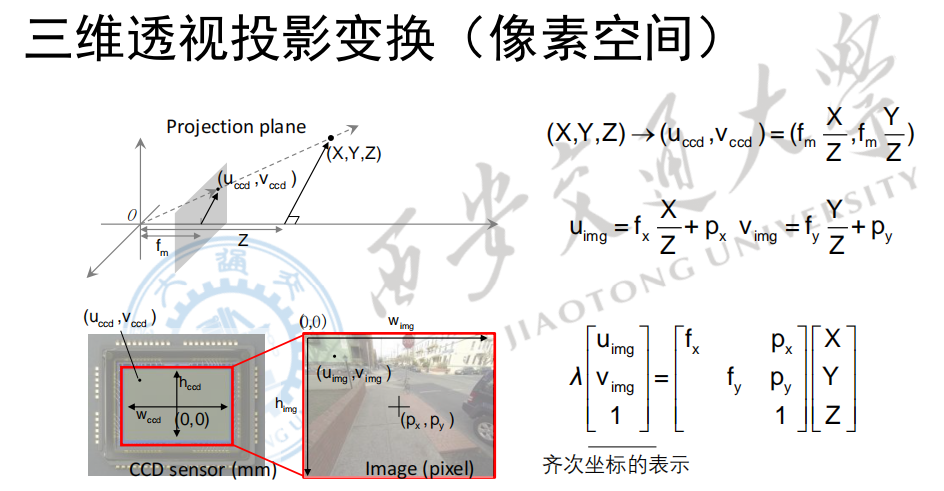
我们接下来把上面的式子进行进一步的变换

$$\begin{align} u_{img} &= f_X\frac X Z + p_x\\ v_{img} &= f_Y\frac Y Z + p_y \end{align}$$ $$\Rightarrow \begin{align} Z\cdot u_{img} &= f_X\cdot X + p_x \cdot Z\\ Z\cdot v_{img} &= f_Y\cdot Y + p_y \cdot Z \end{align}$$

然后把上面的式子向量化之后，就得到了

$$\lambda \begin{bmatrix} u_{img}\\ v_{img}\\ 1 \end{bmatrix} = \begin{bmatrix} f_x & & p_x \\ & f_y & p_y \\ & & 1 \end{bmatrix} \cdot \begin{bmatrix} X\\ Y\\ Z \end{bmatrix}$$

其中，$\lambda$就是某一个的深度信息

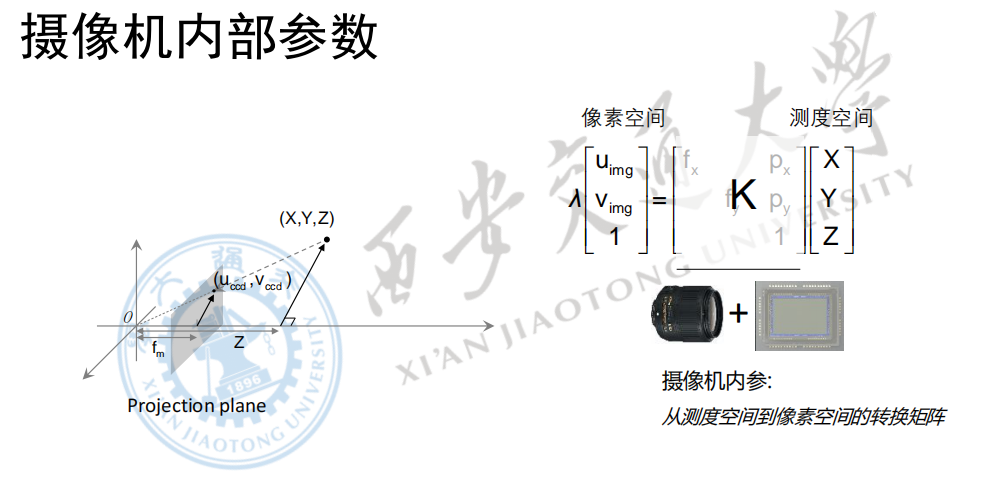
3.5 相机的内部参数

因为上面的矩阵是相机内部的结构决定的，在相机出场的时候就定下来了，因此这些参数又成为内部参数。内部参数完成了从测度空间到像素空间的转换矩阵

3.6 逆变换

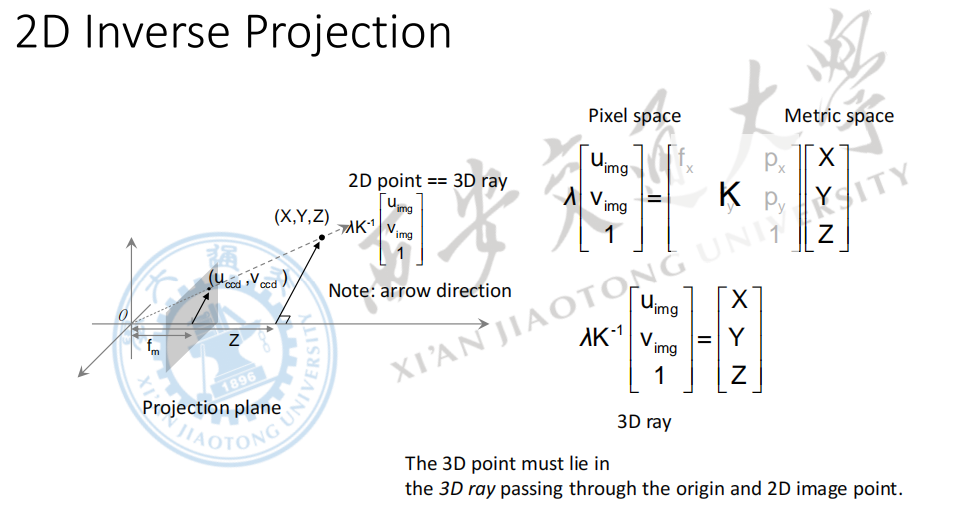
我们扇面完成了从三维平面到像素平面的变换。可是有一个问题就是我们能不能从像素平面还原得到一个点的三维坐标呢？

这个其实是不行的，因为上面在投影的过程中，我们在投影阶段是知道Z/$\lambda$的，但是现在是已经获得了图像，要转换到三维空间中去，这个时候我们是不知道Z的，因此是没有办法进行逆变换得到原始点的。因此我们说投影的过程中损失了深度信息。

我们进行逆变换，只会得到一条射线

4. Dolly Zoom Effect

物体在图像上的大小是由图像上物体的宽度和高度共同决定的，即$+u{img}-u{img}$、$+v{img}-v{img}$两个共同决定

而对于某一个点的$u{img},v{img}$是由下式决定的

那么现在如果$f_m$变大，那么图像就会变大，反之$f_m$变小，图像就会变小。

如果一个人在走向镜头，即$X,Y$变大，我们其实就可以调节$f_m$来保证这个人在图像上的大小不变。但是对应的，除了这个人以外的其他所有物体的大小都将会变小，因为$f_m$变小了。

这种效果在电影界称为Dolly Zoom效应。