本文是Machine Learning 2021 Spring 第八节课的笔记,本节课主要讲解了Neural Network中的Attention机制以及常见的Attention的架构(Module):Self-Attention,此外,Self-Attention也可以像RNN一样实现Sequence的input。

李宏毅ML2021-Spring-8: Self-Attention
有的时候,我们的神经网络需要接受可变长输入作为input。这个时候使用前面说的全连接神经网络或者卷积神经网络就无法处理了。我们需要新的网络架构来处理。循环神经网络(Recurrent Neural Network,RNN)和Self-Attention架构的网络都可以接收边长输入。
另外一方面,我们人类在观察输入(例如图像)的时候,是会把我们的注意力分散到几个关键的地方的,例如鸟嘴、鸟爪等几个地方。换而言之,我们并不是等同对待图片中的所有的地方的,而是有注意力的。这种机制称为Attention(注意力)机制。为网络引入注意力机制的方法(即引入注意力的网络模块/结构/架构)有很多,而Self-Attention就是其中的一种。
因此,本文就将讲解Self-Attention这一网络架构
1. Problem Restatement
1. (Changeable Length) Vector set as input
我们在前面讲解了两种网络架构:全连接网络和卷积神经网络。着两种网络的输入都是一个向量,输出是一个标量(Regression任务)或者类别(Classification任务)

而在有些情况下,我们的输入并不是一个一个的向量,而是一组向量,因为向量与向量之间是具有关系的。例如我们现在有一堆人在进行体育运动的视频,例如一个人在跑步、游泳、踢足球、打篮球等等。再比如前面的Phoneme的分类。在这种情况下,我们的输入就应该是一排向量。稍后给出来更加详细的例子
更复杂的是,有的时候我们输入的一组向量的长度是在变化的。因此对于可变长一组向量的时候,使用全连接网络或者卷积网络就无法处理了。

2. Real Examples
我们接下来举几个真实的可变长的Vector Set作为输入的例子。
A. Sentence as Vector Set
在自然语言处理中,我们往往需要处理一整个句子,即把一整个句子作为输入。如果这个时候我们把一个单词处理为向量,那么这个时候,作为输入的一个句子就是一个Vector Set

具体来说我们是如何把一个单词处理为一个向量的呢?这个方法有很多,例如我们可以直接进行one-hot encoding,这样就得到了一个向量

但是one-hot encoding有很多问题:
- 第一个问题就是每一个向量的长度都需要等于世界上已知的所有单词的数量,因此会造成空间的浪费。
- 其次,one-hot因为用不同的维度来表示单词,因此使用one-hot的话就表示这些词之间是没有关系的。可是我们又知道cat、dog和elephant都是动物,之间是有关系的,而cat和apple是没有关系的,而如果我们使用one-hot encoding的话就无法表示出来这种词之间的关系。
- 还有多音字、一词多义等等问题,这种问题就需要考虑到上下文。
除了one-hot来获得词向量之外,还要一个更加合理的方法来获得词向量,即word embedding。Word Embedding方法给每个词语的词向量都是包含了语义信息的。因此我们如果把Word Embedding得到的每个词语的向量画出来之后,就会发现同类的词语之间靠的就会非常接近。

关于Word Embedding是如何得到含语义信息的向量的,就不是我们今天这节课的要讨论的问题。可以参考李宏毅老师以前的课程链接

总的来说,我们上面将One-Hot和Word Embedding的目的就在于告诉大家,我们是有方法把一个词语转变为一个向量的,并且在这个基础上处理句子就需要我们的模型能够接受一个可变长的vector set作为输入。
B. Audio as Vector Set
我们在进行音频相关的任务的时候,也是把音频作为了一个Vector的Set。例如我们前面的Phoneme Classification的任务。
针对一段音频,我们首先取一个(Sliding) Windows,获得一小段音频,然后对其进行处理,得到一个向量。这个向量一般称为一个frame。而处理得到向量的方法有很多,例如MFCC、Filter Bank等方法

然后我们在把这个window向右滑动一下(所谓Sliding Window),例如10ms,然后计算的到第二个frame的值

通过这样,我们就把一个1秒长度的音频转变为一个100个frame的vector set了。而又因为语音的长度是不定的,因此一段音频对应的vector set的长度其实也是不确定的。
C. Graph as Vector Set
除了句子和音频可以转换为Vector Set以外,Graph也可以用一个Vector Set来表示,例如Social Network,我们把Graph中的每一个Node都当做一个向量。而Node中可以以这个人的姓名、年龄等等作为一个Vector中不同的Dimension。
除了Social Network以外,我们也可以把一个molecule当做一个Graph,而molecule中的atom就可以当做Graph中的Node
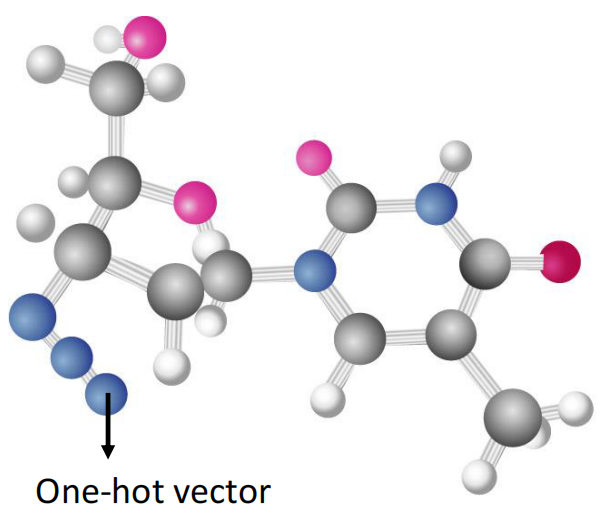
而每一个atom,我们又可以通过one-hot encoding的方式来得到一个向量,所以一个分子就可以表示为一个Vector Set

2. Classified by Output
我们上面说道,我们需要新的一类接受可变长向量组作为输入的模型来处理一些任务,而针对这些模型,我们根据其输出的类别可以把他们分为三类:
- 输出和输入等长
- 输出只有一个值
- 由模型自己决定输出多长
下面我们就结合实际的案例来介绍一下这三类网络和对应的应用
1. 输出和输入等长 (Sequence Labeling)
第一种网络的输出和输入是等长的,这种网络一般都是用于给原始的输入进行打”label”的,例如对于一个句子,我们现在对其中每个词进行词性标注;然后还有我们在第二个作业里的Phoneme Classification,需要给一段语音的所有的vector分类,得到其Phoneme的类别;其次如果是电商的话,我们可以根据Social Network来判断用户(结点,即Vector)对某个商品是否会购买
因此输入和输出等长的任务又称为Sequence Labeling任务
2. 输出只有一个值 (Sequnce Classification/Regression)
第二种情况,我们的输入是一个Vector Set,而输出只有一个值。这种情况就很想我们把输入的Vector Set视为一个整体,然后对其进行Classification或者Regression任务。
因此这类任务又称为Sequence Classification 或者 Sequence Regression任务
例如现在有一个句子,我们可以对其进行情感分析,这个在某个产品上线之后判断用户对其的态度非常好用。然后未来在作业四中我们还会根据一段语音来判断说这段话的人是谁,这也是输入是一个vector set而输出只有一个值的例子。最后就是现在给一个分子,判断这个分子是亲水性还是疏水性。

3. 输出长度由网络自己来决定
有的任务中,我们并不知道我们网络输出的长度是多少,例如在机器翻译中,四个字的中文句子可能翻译成英文有十多个单词,而且不同的人翻译得到的长度也不同。
这种任务又称为Sequence to Sequence的任务,因为输入输出都是一段具有独立意义的Sequence。在作业5中我们会有相关的任务。
经典的Seq2Seq的任务包括有翻译、语音转文字等等

4. Focus of this lecture
本节课要讲的Self-Attention这个网络的架构主要是为了能够让网络接受一个Function Set作为输入,而具体的输出是什么样的这个需要我们自己在self-attention模块之后接自己设计出来的针对任务的(Task Specified)的模型。
因此为了简单起见,我们本节课就以Sequence Labeling任务为载体讲解Self-Attention Module

3. Sequence Labeling as Vector Labeling?
1. Fully Connected Network fails
我们前面说Sequence Labeling的输出和输入是等长的,而输出往往就是给输入进行Labeling,那么我们就会想能不能用前面讲的吃一个vector的模型来对每个vector单独进行Labeling。
例如我们就直接用前面的全连接网络来完成Sequence Labeling

可是这样做会有非常大的问题,例如我们现在就进行词性分析(POS Labeling)这个任务。
例如下面的句子:I saw a saw,这两个saw是不同的词义的,可是如果我们使用全连接或者卷积网络的话输入是一样的,Network是没有理由给出来不一样的输出的。因此这种时候就会有问题。

这个问题的出现,就是我们忽略了Vector Set的Vector之间的相关性,或者说我们忽略了Sequence内在的逻辑。Sequence整体是作为一个整体,其内部最小的unit之间是有逻辑关系的,而我们上面这样做就忽略了这个逻辑背景,因此失败了。
所以为了能够进行弥补这个问题,我们就想,能不让对Fully Connected的Neural Network进行改进,让他能够考虑更多的、上下的Context的数据呢?这其实是有可能的。
2. Neighbor as input
为了考虑一个vector的Context,一个简单的方法就是把这个vector的邻居在一起作为一个input丢给全连接网络

这就相当于我们用一个windows在Sequence上滑动。这个做法我们在作业二中就是这样处理的,我们把当前需要分类的Phoneme和前后各5个Phoneme在一起作为一个input

3. Limitation of Neighbor
可是上面这样把邻居作为输入一起丢入模型还是有问题的,它能考虑到的Context只有一个windows的范围。可是在很多情况下,我们要对一个句子进行词性划分的话是需要考虑很长范围的。例如上面的I saw a saw,如果中间有插入语、定语什么的,句子的长度就长了,这个时候windows只会越开越大。
可是window开大了又有一个问题,那就是边缘的几个vector开window的话前面后面都是没有vector的,所以就会有问题。
其次,考虑上下文的极限就是考虑整个句子,可是如果考虑整个句子的话最终又回到了句子作为一个input是变长的这个问题。
因此,我们不得不就开从模型的端入手,来进行修改
4. Self-Attention
上面,我们铺垫了差不多3500个字,讲解了全连接和CNN的问题,然后又提出了可能的解决方法的问题,最终讲到不得不使用Self-Attention的必要性(Justification of Self-Attention)。下面我们就来讲解Self-Attention具体的操作。
1. Function of Self-Attention
我们先来看一看Self-Attention的作用。Self-Attention一次吃一个Sequence的输入,然后会输出和输入的数量一样的Sequence。
不过不同的是,经过Self-Attention之后得到的Sequence和原输入的sSequence相比,其是考虑了整个句子上下文的Sequence。因此我们然后就可以把考虑了上下文的vector再传入FC中,这样的话效果就会好很多。

然而,并不是说Self-Attention只能用一次,我们完全可以多次、重复进行Self-Attention。即在经过FC之后,再通过一次Attention

这样的话,让Fully Connected的网络专注于处理某一个位置的特征,而Self-Attention着眼于处理全局的特征。
2. About Self-Attention
关于Self-Attention最出名的文章就是谷歌的Attention is all you need。在这篇文章中,Google提出了Transformer这样的结构(Transformer后面会讲)。而Transformer里最重要的一个Module,就是Self-Attention的Module。
Self-Attention其实不是这一篇文章提出来的,而是在很早以前就已经有人提出来了,但是这篇文章是把Self-Attention发扬光大的。

3. Overview of Self-Attention
首先,Self-Attention可以用于第一层,也可以用于中间的层。因此Self-Attention的input可以是input,也可以是hidden layer的output,因此我们用$a^i$来表示输入。

而在接受了这一排输入之后,self-attention输出和输入一样数量的output

需要注意的是,输出的每一个Vector都是考虑了input的整个Sequence的、含有全文Context的输出

4. Step 1: Attention Score
Self-Attention的第一步,就是来计算当前的这个vector和上下文的哪些Vector(为了完成最终的任务)是有关系的。
为了描述这个关系,我们用一个值来进行表述,即attention score

那么现在的问题就是,输入的$a^1$和其他的vector,例如$a^4$之间的attention score该如何计算呢?注意,attention score的计算是有方向的,例如我们这里计算的是$\alpha$是$\alpha^1$对$a^4$的attention score。
具体计算$\alpha$的分数有两种,一种是通过dot product的方式,另外一种是通过additive的方法,注意计算attention score的时候,输入是两个输入的vector,而输出是attention score,因此我们也可以把计算attention score画成一个模块

A. Dot-Product
dot-product计算attention score的方式是给输入的两个向量分别乘以两个矩阵进行变换,这两个矩阵分别称为query矩阵和key矩阵,记为$W^q$和$W^k$,稍后会解释为什么称为$query矩阵$和$key矩阵$。
我们这里因为计算的是$a^1$对$a^4$的attention score,因此我们给$a^1$乘以矩阵$W^q$得到query向量$q$,给被计算attention score的$a^4$乘以矩阵$W^k$得到key向量$k$。
然后让query向量和key向量进行dot product,就得到了$a^1$对$a^4$的attention score

B. Additive
相加计算attention score的方法则是在得到了query向量和key向量的基础上,进行element-wise的相加,然后经过一个activation function,例如tanh函数,然后在经过一个transform就得到了最终的attention score

这两种计算attention score是最经典的计算的方式,实际上还有很多种计算的方式。而一般我们常用的计算attention score的方式就是第一种,即通过dot product来计算attention score。

C. Calculate All Attention Score
接下来,我们就来计算$a^1$对$a^2$、$a^3$、$a^4$四个vector的Attention Score,具体如下。
我们首先用上面说的Dot-Product的方式计算$a^1$对$a^2$的Attention Score

然后同理,我们重复这个过程,直到计算出来$a^1$对$a^3$、$a^4$的Attention Score

在实践中,我们其实也会为了$a^1$计算出来一个key向量,然后计算自己对自己的Attention Score。这样的话方便等一会的向量化计算。因此,$a^1$会计算得到四个Attention Score

最后,在计算完初始的Attention Score之后,还需要进行归一化。因为我们的注意力总和是1,因此这里表示我们把多少比例的注意力分配给了周围的Context
当然,进行归一化的方式还有很多,这里用softmax是没有概率上的意义的,其实也可以别的归一化的方式。有人甚至换成了ReLu,结果效果还更好

5. Context Fusion
在计算得到了Attention Score,或者说Relevance Score之后,我们接下来就是利用这个Attention Score来计算得到含有Context的output。
具体来说怎么做能,我们再通过一个value矩阵$W^v$,然后用value矩阵给每一个input的vector相乘之后进行transform得到value向量,这个value向量就是稍后用于合成输出的向量

这个时候因为我们计算的是$a^1$的输出,因此我们现在把这四个value向量乘以Attention Score之后就得到了含有注意力的value向量。
接下来把这四个向量相加就得到了$a^1$对应的输出

所以通过上面的这些操作,我们就计算得到了$a^1$对应的、含有整个输入上下文的输出$b^1$。
同理,我们对$a^2$进行计算,得到$a^2$对应的输出$b^2$。
首先计算得到$a^2$对四个input的Attention Score,然后经过Softmax归一化得到Attention Score。

然后我们把这四个值和四个value向量相乘得到然后加和得到$a^2$对应的输出$b^2$

我们在计算的时候,发现$b^2$的计算和$b^1$完全无关,因此我们进行计算的时候是可以并行计算同时得到所有的四个输出的。

所以并行计算就可以得到所有的四个输出。
5. Vectorization
我们上面介绍完了Self-Attention所有的操作。在最后的部分我们说道,其实可以并行计算同时得到四个输出$b^1$,$b^2$,$b^3$和$b^4$。
那么我们下面就讲讲如何对向量化Self-Attention的计算,以实现并行计算。而计算得到所有输出大体上分为两步:
- 计算得到K、Q、V
- 利用K、Q、V计算Attention Score
- 利用Attention Score计算得到输出
1. Vectorization of query, key and value vectors
我们首先对query vector的计算进行向量化。
对于四个输入$a^1,a^2,a^3,a^4$而言,我们计算得到四个query向量就是用用一个query矩阵和四个输入向量分别相乘。如下图所示

然后我们再同样计算得到$q^2,q^3$和$q^4$

那这个时候,我们就可以把四个$a$和$q$拼起来,成为两个矩阵,称为$I$和$Q$(input和query)。在计算$Q$的过程中,Q是计算得到的,$I$是输入的矩阵,而$W^q$是网络的参数,因此网络需要学习的就是$W^q$这个矩阵
同样,我们接下来向量化计算key向量的过程。计算key向量和计算query向量一样,使用一个key矩阵左乘向量即可,因此我们仿照上面的步骤,进行计算。

类似的,我们记所有的key向量拼成的矩阵为$K$,而参数矩阵$W^k$就是需要学习的参数
同理,我们向量化value向量的计算。
过程还是一样的,我们直接略过。需要注意的是,我们计算的value vector拼起来得到的矩阵记为$V$。而网络的参数$W^v$就是第三个需要学习得到的参数

最后,我们向量化计算query、key和value,最后得到$K,Q,V$三个矩阵其实就是通过三个参数矩阵$W^v,W^q,W^k$,这三个矩阵是我们稍后需要Update的对象。

2. Vectorization of Attention Score
我们接下来计算Attention Score。Attention Score因为是考究方向的,因此我们用$\alpha_{i,j}$表示输入$a^i$对$a^j$的Attention Score。
我们计算Attention Score的时候使用$a^i$的query向量和所有输入的key向量进行Dot-Product。而Dot-Product即向量转置相乘。
因此,现在计算$\alpha{1,1}$的即:$\alpha{1,1}={k^1}^T\cdot q^1$,用图来表示的话,为了减少符号,所以横过来表示转置

同理,我们可以计算$a^1$对其他三个输入的Attention Score,得到$a{1,1},a{1,2},a{1,3},a{1,4}$四个Attention Score

这四个值其实也可以通过向量化的方式来计算,即把四个key向量hstack起来,那么得到了$a^1$的Attention Vector

那么同样,我们用$q^2$来计算$a^2$的Attention Score,那么最后就会得到下面的式子

同理,我们重复计算就得到了$a^3$和$a^4$的Attention Score

而计算得到16个Attention Score的过程,可以视为两个矩阵相乘,即
最后,我们还需要对某一个输入的四个Attention Score进行归一化,就得到了最终的16个Attention Score

3. Vectorization of Output
我们接下来计算最终的输出。
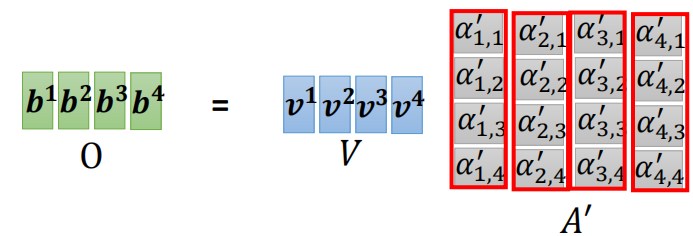
计算输出就是用前面计算得到的四个Attention Score和四个Value Vector分别相乘,然后相加得到最终的输出。例如把$a{1,1},a{1,2},a{1,3},a{1,4}$和$v_1,v_2,v_3,v_4$分别相乘然后相加就得到了$b^1$,而$b^1$的计算图示如下

注意,图中是把$V$这个矩阵按行分块视为一个向量,所以$V$左乘$A’$的第一列就得到了$b^1$。在实际的计算时候,是要进行广播操作的。
那么我们用$V$和$A’$的每列分别相乘,就得到了最终的输出矩阵$O$
4. Summary
最后我们对上面的整个过程进行一下总结

我们就会发现,Self-Attention进行了那么多复杂的计算,其实最后需要学的参数很少,只有3个,即$W^q,W^k,W^v$

6. Multi-head Self-Attention机制
上面讲完的Self-Attention机制其实只是最简单的Self-Attention,而近些年有对Self-Attention提出改进的方法,其中之一就是Multi-head的Self-Attention。
Multi-head Self-Attention对Self-Attention提出的改进的角度就是,Self-Attention抽取到的relevance或者说Attention只是从一个角度出发考虑的,例如现在进行词性分析的话,现在计算得到可能只是从与谓语的关系(副词、主语还是宾语)这个角度出发来分析的。而有的时候我们可能需要从多个角度来进行分析,例如分析该词对主语、宾语(定语),对谓语的关系。
因此我们可能需要多种不同的Attention。所以Multi-head的Self-Attention就是实现了多个Attention。
1. Multi query、key and value vectors
首先,Multi-head的Self-Attention和Single Head的一样,都是先针对一个vector计算得到query、key和value三个向量
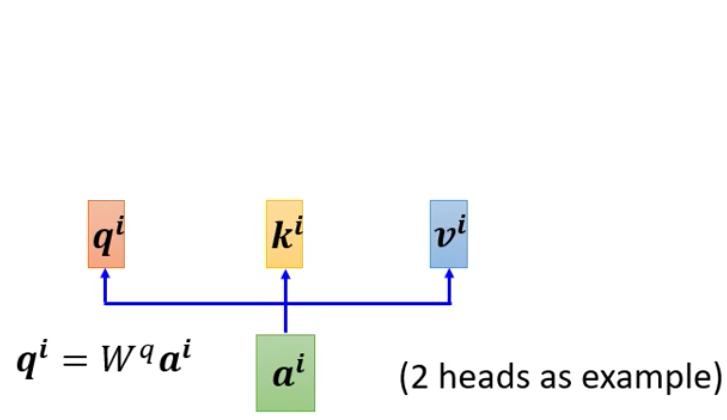
而为了获得两种Attention,Multi-head就是给每一个输入多套query、key和value向量。

而如何获得多个query、key和value呢?以query向量为例,就是给一开始得到的$q^i$乘以两个向量

同理,计算得到两个$k$和$v$都是用两个矩阵。
2. Multi Output
然后假设我们现在只有两个输入来计算Multi-head的Self-Attention
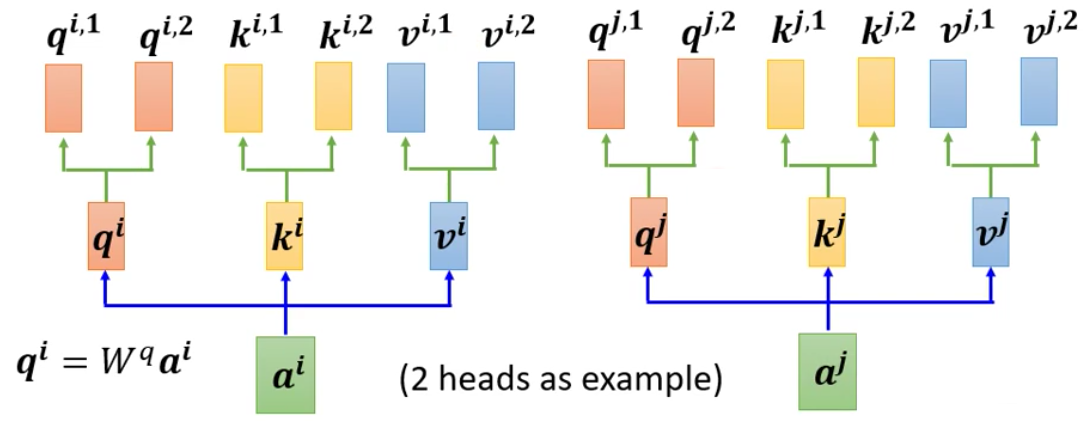
我们接下来计算Attention,一般都是用某一套来独立计算,例如现在$q^{i,1}$计算Attention Score,那么就不要管$k^{i.2}$和$v^{i,2}$,对$q^{i,2}$也是同理

同理,针对第二套参数我们也计算得到一个output

3. Final Output
最后,我们再用一个矩阵得到最终的输出

7. Positional Encoding
Self-Attention最终可以获得一个含有上下文信息的输出,然而Self-Attention的另外一个缺点就是它缺少了这个vector在整个句子中的绝对的位置信息。例如大多数时候,动词都不会出现在句子的开头而是处于中间或者结尾(主谓宾或者主谓结构的句子)。
那这个时候该怎么办呢?办法就是如果我们觉得位置这个信息是比较重要的话,我们就把位置的信息塞入到Self-Attention中去。这个技术就成为Positional Encoding。
Positional Encoding具体来说就是给每一个vector一个包含位置信息的vector,然后把它加到原始的输入上去就行了

求取位置编码$e$的时候,在Attention is all you need中,是手工设计的

而目前,Positional Encoding获得的方法仍然是尚待研究的问题,不过目前也有人尝从数据中自己学出来

8. Self-Attention Application
Self-Attention运用的领域非常广,下面就将进行介绍
1. NLP
2017年Transformer最早被提出是运用在NLP领域,而对应的文章Attention is all you need就是把Self-Attention发扬广大的文章。进一步在2018年就有了bert这个模型

2. Speech
Self-Attention在语音领域也有所应用,不过有一个问题就是我们说的一句话,转换成Vector Set的话就会非常大,向量的维度往往会上千。
那么我们这个时候的Attention Matrix就会很大,导致塞爆Memory。

所以就需要进行一下修改,而Truncated Self-Attention就是对其进行了修改之后得到的用于Speech领域的Self-Attention
具体来说,其思路就是一次让模型只接受一个局部作为输入,而非看所有的输入,并且看到了后面就会丢弃掉前面的输入

而为什么我们认为只需要看一个片段即可,那么这个取决于我们对问题的立即,即我们的Domain Knowledge。例如Phoneme的识别只需要局部的语音即可。
3. Image
Self-Attention还可以用于图像领域,因为一个图像也可以视为一个Vector Set。例如我们把一个Pixel上的RGB三个颜色视为一个Vector,那么一张图片(以下面的鹰为例)就是5*10个向量

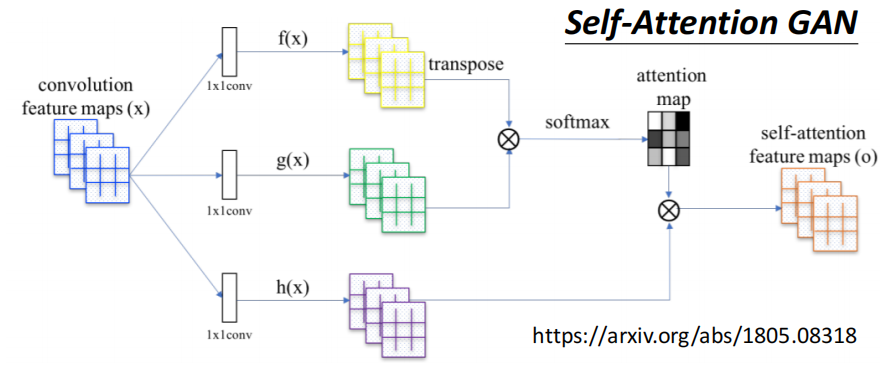
而实际运用Self-Attention到图像领域的工作有Self-Attention GAN和DETR
Self-Attention GAN用于生成任务
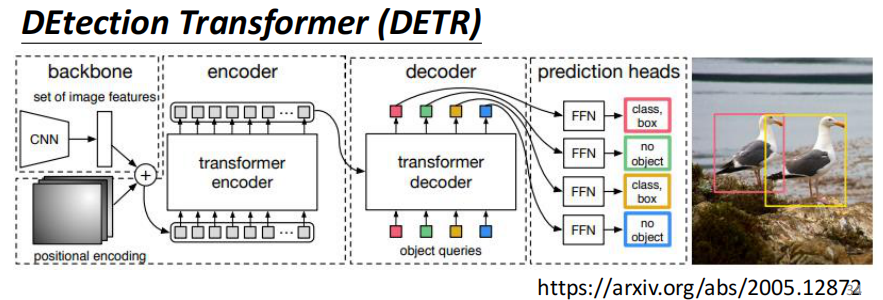
DETR将Self-Attention运用到Detection任务
3. Graph
我们前面还说过,Self-Attention可以用在Graph上面,Node是作为一个Unit嵌入在Network的Context下面的,因此我们这个时候也可以用Self-Attention来抽取上下文的信息。
我们的Attention Matrix只需要计算有边相连的Node,因为没有边相连的Node就暗示两个Node之间没有关系,所以我们就没有必要计算没有边相连的两个Node之间的Attention Score

8. Self-Attention v.s. CNN
我们接下来来看看Self-Attention和我们前面讲的CNN之间的关系。
我们按照上面说的,把一个pixel当做一个Vector,那么这个时候Self-Attention考虑的就是两个Pixel之间的关系

而CNN则是只考虑一个Receptive Field范围内的input

因此,CNN就是简化版的Self-Attention,只会学习一个Receptive Field内的关系(Attention Score)。反过来说,Self-Attention是升级版的CNN,其Receptive Field是可以自己学的
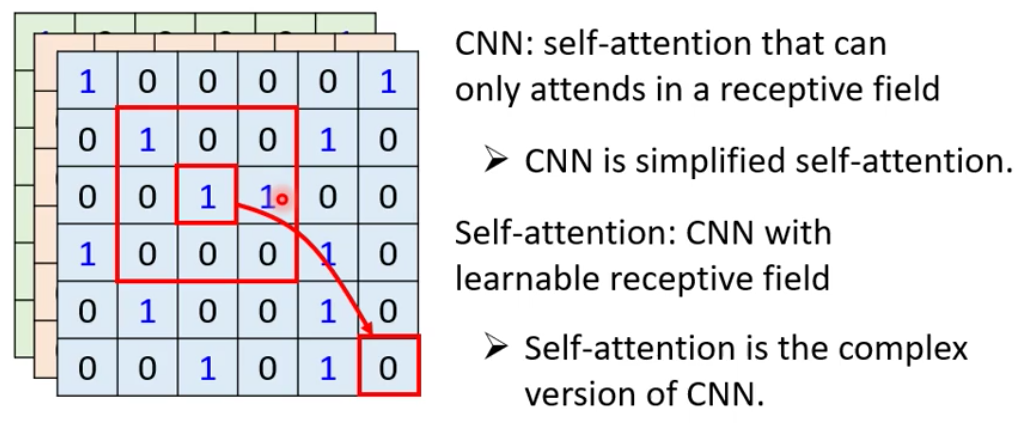
更下详细的解释可以在这篇paper中看到:On the Relationship between Self-Attention and
Convolutional Layers。这篇Paper中以严谨的数学证明了Self-Attention是CNN的超集,而对Self-Attention加以适当的限制,其就退化为了CNN,并且训练得到的结果一致

我们前面说过,可以表示更大的Function Set的模型相比于小的模型更加难Train,但是可能会存在更优的参数。因此对于CNN和Self-Attention来说,就是Self-Attention比CNN更加难train,但是如果Train的好了最后性能有可能由于CNN。
而实验是支持这个理论的,在数据量比较小的时候,CNN轻易的就可以得到很好的表现,可是随着数据量的增加,最终Self-Attention的模型的表现超过了CNN

9. Self-Attention v.s. RNN
我们最前面说过,可以接受边长输入的模型除了Self-Attention以外还有RNN。
RNN有一个Memory,然后RNN的block每次吃Memory和input得到更新的Memory,然后对更新的Memory通过一个FC得到输出。
而这个Memory又称为Hidden Vector,因此RNN传递Sequence的信息就是通过Hidden Vector在RNN内部的传递。

而RNN和Self-Attention干的事情是一模一样的。两者的input和output都是Sequence

可以有一个问题就是,RNN只考虑了从前往后的Context,而Self-Attention则是考虑了前后的Context,不过这个问题RNN其实可以解决。其次RNN是需要前一个更新完的Memory,因此RNN是无法并行计算的。

而且,RNN还存在遗忘的问题,就是第一个input的Context在中间已经被更新好几次了,所以计算到最后一次的时候都已经遗忘的差不多了,因此后面的input很难会考虑到很前面的Context,而这问头对于Self-Attention来说就不成立

因此现在更加常用的就是Self-Attention,虽然Self-Attention更难Train。

现在其实也有文章在讨论RNN和Self-Attention的关系,例如这篇文章:Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
10. To Learn More
最后,关于Self-Attention其实有非常非常多的变形,因此有很多的Paper对其进行研究,例如减少Self-Attention的计算量等等。针对Self-Attention不同的缺点,就有不同的Paper来进行研究,因此构成了关于Self-Attention非常多的研究。
下面就是两篇关于Self-Attention的综述文章




