本文是Machine Learning 2021 Spring 第六节课的笔记，本节课主要讲解了利用深度学习进行分类使用softmax以及cross-entropy背后的原理。

具体而言，本文首相讲解Probabilistic Generative Model，然后过渡到Logistic Regression，最后在讲解完前面两个模型之后，引出深度学习使用softmax个cross-entropy背后的原理

李宏毅ML2021-Spring-6: Classification (Long Version)

前面的Classification的short-version只是讲解了该怎样进行操作，才可以让神经网络完成分类这件任务而避免掉直接用回归的模型来硬解分类可能带来的问题。然而我们并没有将这些操作的原理，可是只有知道了原理才能够更好的帮助我们来进行理解。因此在Classification的Long Version的版本中，将会讲解Classification背后的原理。课程比较长，有3个小时左右。

我们下面假装不知道什么是Classification，然后来进行讲解😂。注意，让神经网络进行分类这件事在推导的时候其实引入了概率，因此后面会涉及到概率论的知识

1. Introduction to Classification

在讲解Classification前，我们需要知道什么是Classification以及Classification的运用

1. What is Classification

我们在前面的机器学习的介绍中说道，机器学习其实就是让机器自己去找函数。不同的任务找的函数不一样，而Classification这个任务要找的函数，他的输入是一个物体，object $x$，而他的output是这个object是属于哪一个class，n个class中的哪一个

这样的任务其实很容易就能够找到很多，例如：

• 金融上，需要根据一个人以往的借贷的历史等因素来判断到底该不该给这个人放贷。因此，金融上Classification模型的input是这个人的收入、储蓄、职业、年龄、过去的借贷历史等等，而output就是要不要借钱给这个人

  

• 在医疗诊断领域，可以用一个Classification来对一个病人的疾病进行Classification。因此，医疗上Classification模型的input就是某个病人现在的症状、年龄、性别和过去的医疗历史等等，而output就是这个人患的什么病

  

• 此外还可以进行手写字的识别，例如手写一个汉字，然后识别出来这个字是什么。这个其实也是一个Classification的任务，因为常用汉字有8000多个，因此这个就是一个8000个class的Classification任务

  

• 还有人脸识别，和人脸分辨不同，分辨只需要区别出来这是一张人脸即可，而人脸识别则还要识别出来这个人脸是谁。因此，人脸识别的Classification的model的input是人脸的图片，而输出则是人脸对应的人（的名字）

  

2. Example Application

下面我们对Classification的讲解都将结合一个例子来进行，因此下面先介绍一下这个例子的background。

在神奇宝贝中，每个神奇宝贝都是有一个自己的属性，例如普通系、火系、水系等等

那么我们现在的任务的就是要input一只神奇宝贝，output这只神奇宝贝的属性，例如：

• 输入一只皮卡丘，输出雷属性
• 输入一只杰尼龟，输出水属性
• 输入一只妙蛙种子，输出草属性

那么现在，我们面临的第一个问题就是模型如何输入一只神奇宝贝。我们知道模型的input都是数字，因此我们的第一步其实就是把神奇宝贝数值化，用一些数值来表示一只神奇宝贝，然后把他们放到神经网络里面。

那么我们用哪些数值来描述一只神奇宝贝呢？

其实每只神奇宝贝都是有一些可以数值化的特性，例如：

• 强度（total）：描述了总体上一只神奇宝贝有多强
• 生命值（HP）：描述了一只神奇宝贝血量有多高
• 攻击力（Attack）：描述了一只神奇宝贝的攻击能力
• 速度（Speed）：决定了两只神奇宝贝相遇的时候谁先攻击
• 防御力
• 特殊攻击力
• 特殊防御力
• ……

那么现在我们就可以用这些值来描述一只神奇宝贝，例如皮卡丘

因此，现在对于一个皮卡丘，我们就可以用这七个数值来描述。因此我们现在要研究的，就是能不能通过这七个数字，把一个长度为7的代表神奇宝贝的向量丢到模型里去，然后模型就可以给出来这个神奇宝贝的属性

3. Why study this

我们可能会想，为什么要研究为神奇宝贝的属性进行分类，那么其实，这个是有“非常重要的原因“的。

1. 首先，不同属性的神奇宝贝在相遇的时候其实是有属性的克制的。例如格斗系大普通系，伤害就会翻倍。因此能够准确的判断对方的神奇宝贝的属性能够帮助我们获胜

   

2. 另外一个原因就是，并不是所有的神奇宝贝都是有图鉴的。例如在李宏毅老师小的时候一共只有150多只宝可梦，6种属性。但是现在却有800多只、18种属性。因此有一个预测的模型能够帮助我们判断神奇宝贝的类别还是很有必要的

3. 让我们学习Classification任务啊😂

4. Dataset preparation

我们因为要做机器学习的任务，因此我们需要有数据让我们的模型来学习，因此我们收集到的数据其实就是下面这样的一个一个的pair

pair中的一个神奇宝贝的七个值作为$x$而对应的这个神奇宝贝的属性$\hat y$作为这个神奇宝贝的label

然后现在一共有800只神奇宝贝，我们取其中的前150只作为训练数据，用后面的神奇宝贝作为测试数据。这样的话刚好可以模拟不断发现新的神奇宝贝的、对新的神奇宝贝进行分类的过程。

2. How to do Classification？

上面我们介绍了我们的case，那么接下来我们就该讲解该怎么样来解这个问题了

1. Classification as Regression？

前面我们讲了Regression的问题，那么有人就想，现在我们会Regression的任务而不会Classification的任务，因此我们能不能把Classification的任务当做Regression来硬解。

例如我们现在就在两个class中进行分类。那么在训练阶段，让所有的example的label的值要么是1，要么是-1。而在测试阶段，模型的输出是一个consecutive的number，因此，我们就看这个值是接近1还是-1，然后来判断属于哪个类。

2. Problem of Classification as Regression

可是，上面这种做法其实是有问题的。我们举下面的例子来进行讲解

A. Panelize too correct example

假设我们的模型只有一层，即

$$y=\vec w \times \vec x + \vec b = \begin{bmatrix} w_1\\ w_2 \end{bmatrix} \times \begin{bmatrix} x_1 & x_2 \end{bmatrix} +\vec b$$

那么其实，我们的模型学的就是这个函数

$$y=w_1x_1+w_2x_2+b$$

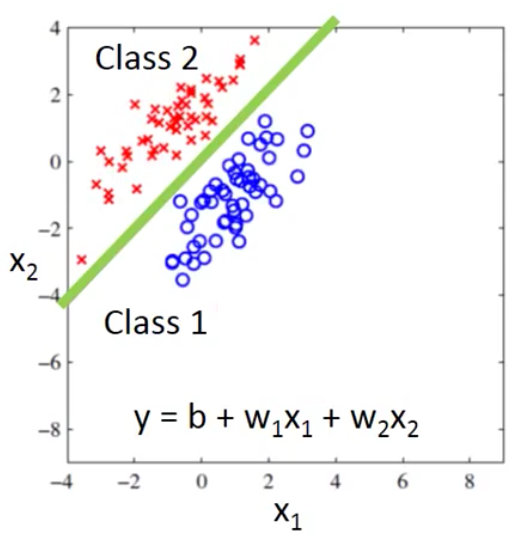
那么我们现在就想，从Regression的角度来说，蓝色这一类的example输入到模型之后，输出越接近-1越好，而红色这一类example输入到模型之后，输出越接近1越好。

那么，我们的模型很有可能学到下面的这个函数，即$b+w_1x_1+w_2x_2=0$这条线里的参数（记为$b’,w_1’,w_2’$）

那么此时我们的模型就是$y=b’+w_1’x_1+w_2’x_2$，这样的话，当class 1中的example被输入之后（注意，每一个example有两个feature），那么得到的输出就会大于0，因此就会接近1。而class 2中的example被输入之后，就会小于0，接近-1。这个就是我们如果用Regression的方法处理之后得到的模型

可是这样做有一个问题，就是如果我们现在多了一些新的数据的话，由于我们在Regression中用的损失函数是MSE，而MSE计算的是到线上的距离，因此我们原来学的线就会往下偏，模型最终学到的就是紫色这条线的参数，这样就会造成一些原来分类很好的example被错误的分类

然而，我们用眼睛的直觉看就知道，绿色的线要更好。

因此，导致这样的问题发生的原因就在于我们的Regression的损失函数不适合Classification的任务。其实就印证了我们前面说的，不同的任务Loss Function不一样。

上面的这个例子中，紫色的解是对Regression来说比较好的解，而这个解其实并不适合Classification

用Bishop的机器学习的书中的话来说，Regression的Loss Function会乘法那些过于正确的点

B. Similarity of different classes

另外一个问题就是我们如果用一个数字来表示一个类别的话，那么在多分类的时候其实就会人为的引入多个不同的类之间的相似性

这个问题其实在前面就讨论过了，这里就不在强调了

3. Ideal Alternatives

我们先以二分类为例，讲讲我们预期的、理想的模型。上面的问题发生的原因首先在于用一个数值来表示一个类，其次在于用Regression的方法硬解Classification。

因此首先，我们理想的Classification模型对应的函数就不用具体的值来表示类别，大于0则表示是类1，否则就是类2

其次，我们的损失函数也要进行修改，相比于距离，我们直接用错误率来作为Loss

最后，由于我们上面的Function和Loss Function其实都是没有办法微分的，因此还需要我们自己去寻找对应的求解的方法

对应的方法有：Perceptron、SVM等等，不过因为我们今天关注的是如何使用神经网络来求解Classification问题，因此我们今天不会讲他们

而由于神经网络找最佳的函数是通过Gradient Descent来进行的。又由于这两步不可微，因此我们就要找一个替代的solution，使得Gradient Descent可行。

下面的这个solution我们首先从概率的角度来进行讲解，最后会将为什么从概率的角度来说这个solution也是符合机器学习定义的，即这个solution也是机器学习的方法之一，以及如何把它用到神经网络上

3. Probabilistic Solution

我们下面首先通过一个例子来引入用概率的方法求解分类问题的办法，然后再正式的进行讲解

1. Preparedness

我们首先看下面的一个例子

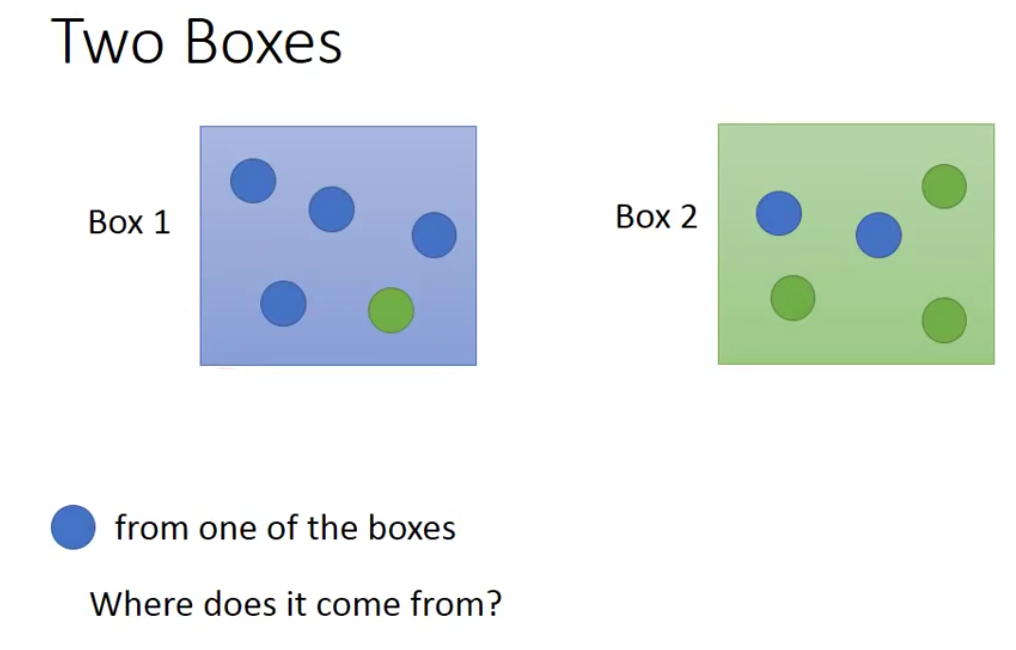
我们现在有两个盒子，每个盒子里都有蓝球和绿球。现在从两个盒子中的一个抽一个球出来，发现是蓝球。问这个蓝球来自与两个盒子的概率分别是多少

如果我们用频率代替概率的话，那么全贝叶斯公式得到蓝球的来自盒子1的概率计算如下

来自盒子2的计算同理，这里就不列出来了。

那么为什么要讲这个例子呢？

我们把每一个球当做example，而盒子当做class。那么我们现在的问题就是，给定一个输入$x$（一个球），现在求这个输入$x$来自于两个类（盒子）的概率

为了使用贝叶斯公式进行计算，我们首先需要知道随便给一个输入，他是class 1的概率，即$P(C_1)$以及对应的，是class 2的概率，即$P(C_2)$。然后还有从class 1中抽出我们现在考虑的$x$的概率$P(x|C_1)$，以及从class 2中抽出我们现在考虑的$x$的概率$P(x|C_2)$。

在有了这些概率之后，我们就可以计算出来$x$是属于class 1的概率了。同理也能够求解出来$x$是class 2的概率。

那么问题的关键就在于如何求解出这四个值。因为我们是机器学习的model，因此我们其实是有Training Data的，因此我们就希望能够从Training Data中的数据来估计这四个概率。而上面这一套理论，统称为generative的model。

为什么称为generative的model呢，就是根据贝叶斯公式，我们在得到了分布之后就可以自己产生一个example。关于这点，我们在后面会更加详细的进行讲解。

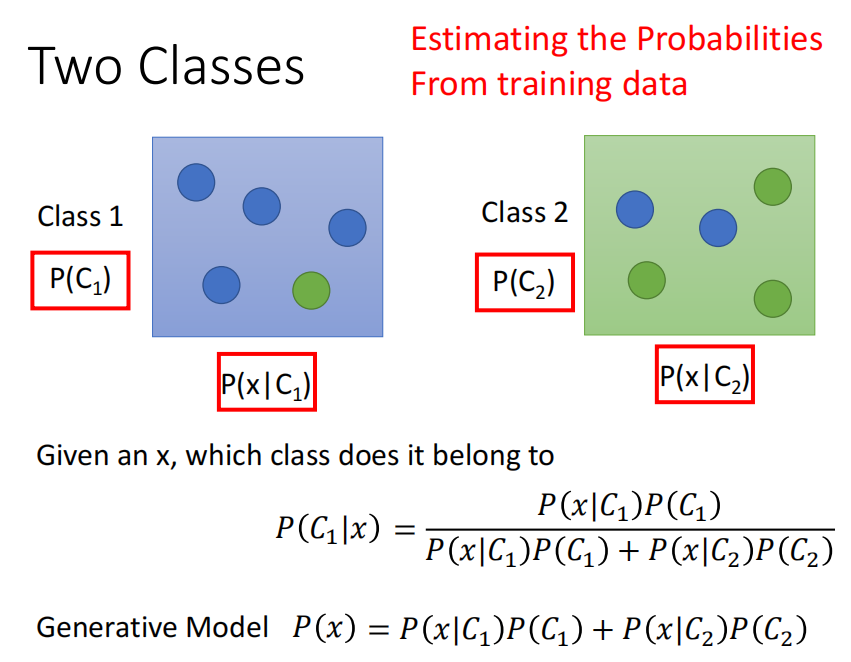
因此，现在我们要计算一个object $x$属于某个类，例如$C_1$的概率，即$P(C_1|x)$。则计算的关键就是计算:$P(C_1),P(C_2)$以及$P(x|C_1),P(x|C_2)$这四个概率。

下面我们就分别来计算这四个概率

2. Prior

我们首先计算$P(C_1)$和$P(C_2)$这两个概率，这两个概率称为Prior，即先验概率。

什么是先验概率

---

回答一（摘自知乎用户Agenter的回答）：

这几个概念可以用“原因的可能性”和“结果的可能性”的“先后顺序”及“条件关系”来理解。

下面举例：

隔壁老王要去10公里外的一个地方办事，他可以选择走路，骑自行车或者开车，并花费了一定时间到达目的地。在这个事件中，可以把交通方式（走路、骑车或开车）认为是原因，花费的时间认为是结果。

若老王花了一个小时的时间完成了10公里的距离，那么很大可能是骑车过去的，当然也有较小可能老王是个健身达人跑步过去的，或者开车过去但是堵车很严重。若老王一共用了两个小时的时间完成了10公里的距离，那么很有可能他是走路过去的。若老王只用了二十分钟，那么很有可能是开车。这种先知道结果，然后由结果估计原因的概率分布，$P(交通方式|时间)$，就是后验概率。

老王早上起床的时候觉得精神不错，想锻炼下身体，决定跑步过去；也可能老王想做个文艺青年试试最近流行的共享单车，决定骑车过去；也可能老王想炫个富，决定开车过去。老王的选择与到达目的地的时间无关。先于结果，确定原因的概率分布，$P(交通方式)$，就是先验概率。

---

回答二（摘自用户风铃猫的回答）

太长不看版：

先验分布是你瞎猜参数服从啥分布

后验分布是你学习经验（已经获得结果）后有根据地瞎猜参数服从啥分布

因此，我们这里说的先验概率其实就是有一个object $x$，然后这个$x$是class 1和class 2的概率

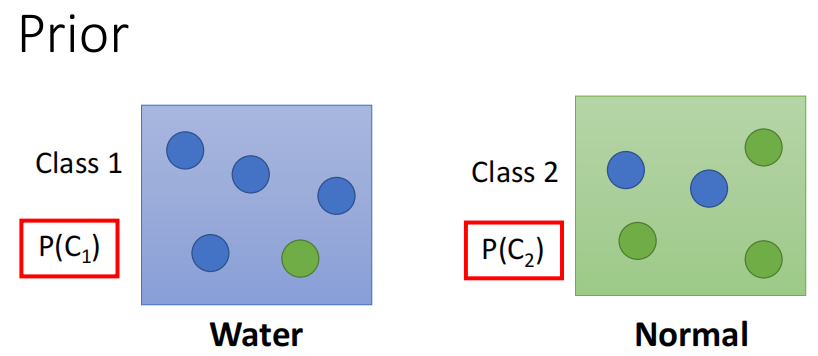
为了获得这两个先验，我们凭空的猜是肯定不行的。由于我们是机器学习的方法，因此我们就从训练集上来获取这两个先验。我们前面说我们以一个二分类为例，那么我们不妨就用神奇宝贝中的水系和普通系的神奇宝贝进行分类。用所有编号小于400的神奇宝贝作为训练集，然后编号大于400的神奇宝贝作为测试集。

我们这里暂时先考虑二分类，因此我们的训练集就是编号小于400的，为水系和普通系的神奇宝贝。我们用频率来代替概率的话，那么得到的先验就是

3. Probability from class

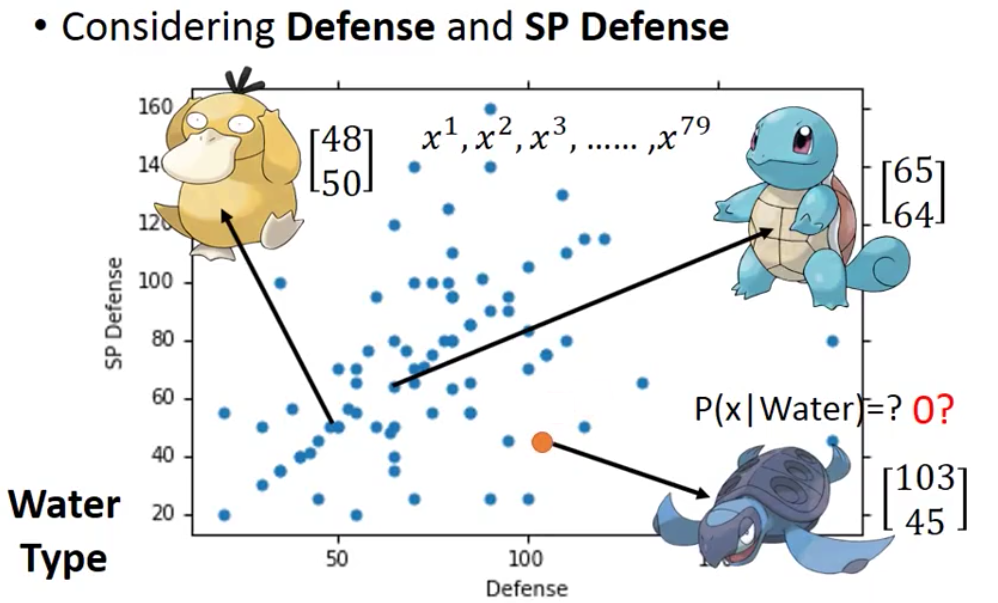
在有了先验概率之后，我们接下来需要计算的，就是$P(x|C_1)$和$P(x|C_2)$。这两个概率表达的含义就是从class 1的所有神奇宝贝中随机抽出来一只神奇宝贝，得到它是object $x$的概率和对应的从class 2中得到object $x$的概率。例如下面，$x$表示圆盖海龟，$C_1,C_2$分别表示水系和普通系的神奇宝贝，那么$P(x|C_1)$就表示从水系神奇宝贝抽出来一只神奇宝贝，它是圆盖海龟的概率。

A. 不能用频率代替概率

这两个概率我们可能的一个想法就是和上面计算先验一样，用频率来代替概率。可是这样做其实是有问题的。因为在测试的时候，我们有79只神奇宝贝，那么可以用1/79作为从某个类中sample得到某个神奇宝贝的概率。

可是在测试的时候，我们的测试的example并不在训练集中，那么这个时候用频率来估计概率就不行了。例如上面的圆盖海龟就不是编号前400的水系神奇宝贝。

因此，我们在获取某个类中获取某个神奇宝贝的概率的时候，就不能用频率来估计概率。下面用图像来更加形象的说明

我们上面说道，为了描述一个神奇宝贝，我们可以用一个长度为7的向量来实现。换而言之，我们用一个长度为7的向量来表示一个神奇宝贝

由于七维点画不出来，因此为了能够画出来，我们这里只选取其中的两个feature，这样的话就可以用二维平面上的一个点来表示一个神奇宝贝。

那么我们真的把79个水系的神奇宝贝画出来在图上，就是下面的样子

我们这里只用了两个轴来表示，就是防御力和特殊防御力。例如下面的可达鸭和杰尼龟

上面说的不能用频率代替概率就是指，Training里可能包含可达鸭和杰尼龟的数据，因此我们这个时候用频率作为概率还是可以得到一个概率的。可是在测试阶段出现了新的圆盖海龟，他并不在我们的训练集中，因此就用频率作为概率的话的概率就是0，这就与事实违背了

因此，我们就需要想办法来根据已经有的神奇宝贝，估测从水系的神奇宝贝挑一只出来，它是圆盖海龟的概率到底是多少

B. 假设为高斯分布

我们无法用频率来代替概率，那么我们下面就需要用别的方法来得到概率。

一个可行的思路就是，我们想想说这79个水系神奇宝贝其实都是冰山的一角。我们想想水系的神奇宝贝是服从正态分布的。因为我们一个神奇宝贝是用了七个特征值来进行描述，因此水系的神奇宝贝其实是从一个7维的Gaussian Distribution中sample得到的。

因此我们这里的防御力和特殊防御力两个值各自都服从一个Gaussian Distribution，因此两个维度在一起就服从一个联合的Gaussian Distribution。

因此，我们下面图里的79个点其实就是对Gaussian Distribution进行了79次sample之后得到的值。这个也非常好解释，因为在Gaussian Distribution中，中间部分sample到的概率要大一点而sample出圆盖海龟的概率会小一点，但是也不是0

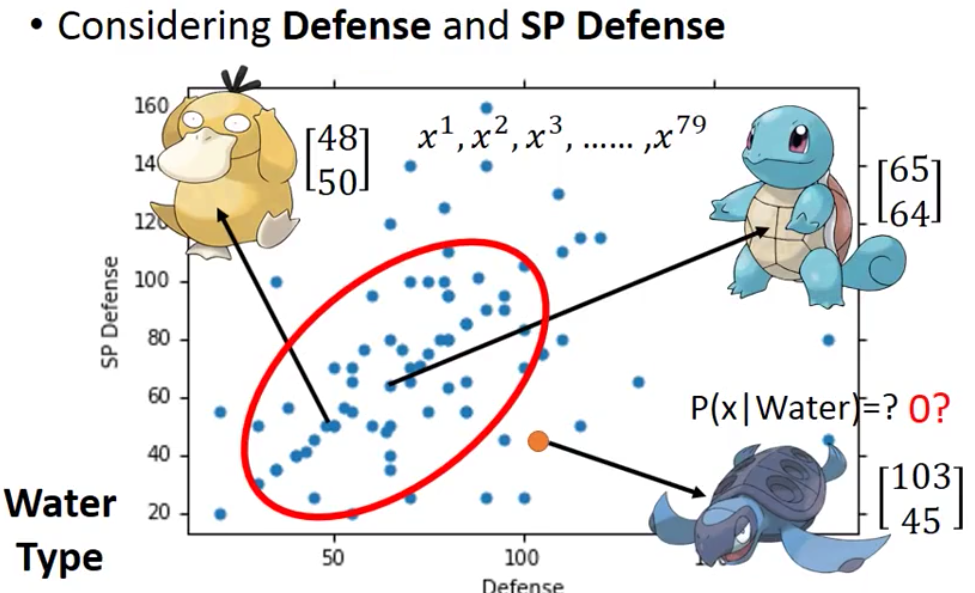
因此，我们现在的问题就从如何确定一个从水系神奇宝贝随机抽出来一只神奇宝贝，它是圆盖海龟的概率成了如何找到水系神奇宝贝的Gaussian Distribution

我们稍后再将如何获得这个分布，假设我们现在已经有了这个Distribution了（为了章节的完整新，因此关于Gaussian Distribution的一些性质放到下一小节）

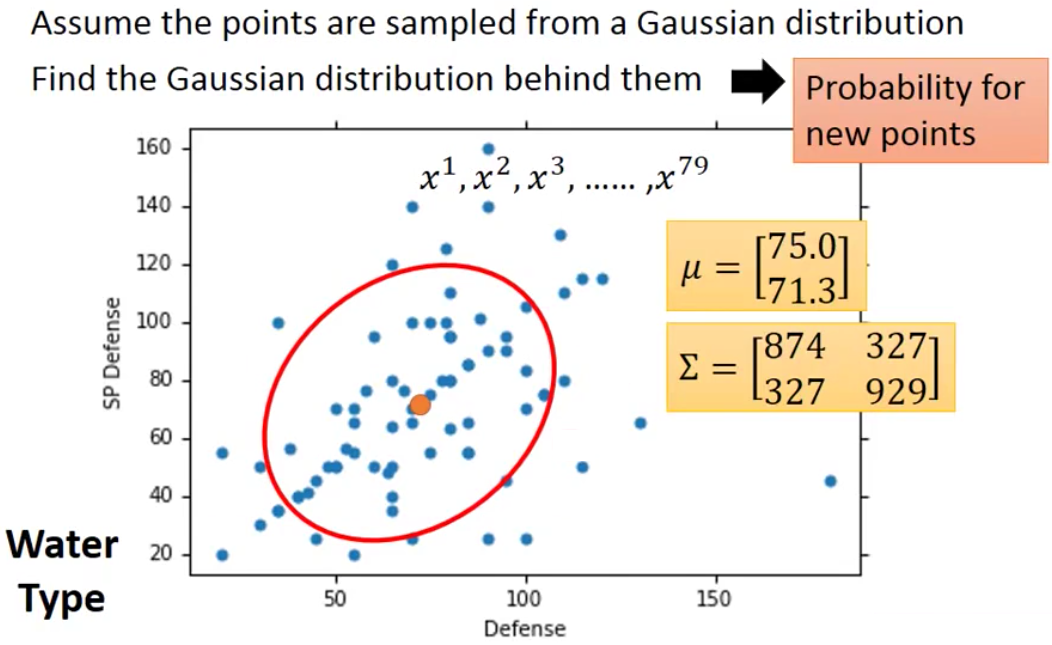
那么根据$\mu$和$\Sigma$就可以写出来这个Gaussian Distribution的expression。然后现在当新的、不在training set里面的$x$来了之后，我们就可以根据这个expression来进行计算

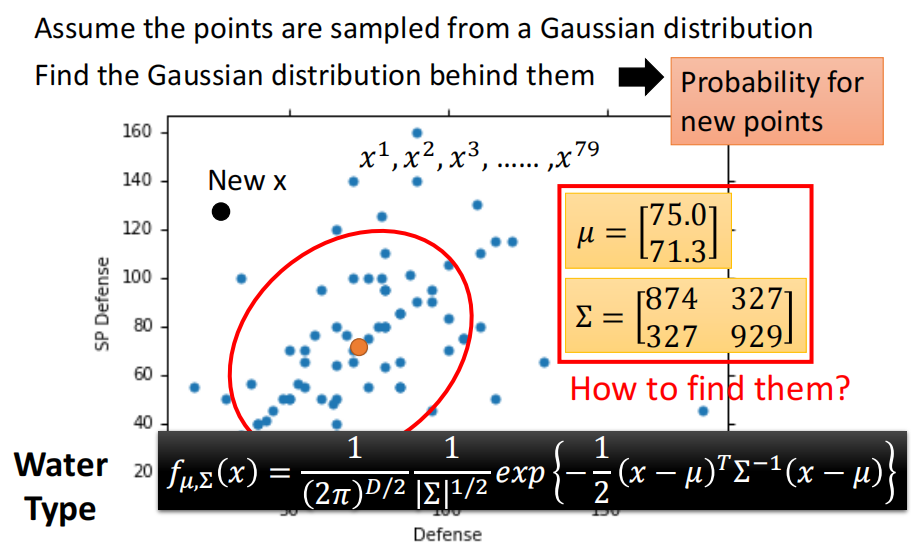
因此，我们就可以得到$P(x|C_1)$和$P(x|C_2)$，即

$$P(x|C_1)=f_{\mu_1,\Sigma_1}(x)$$ $$P(x|C_2)=f_{\mu_2,\Sigma_2}(x)$$

C. About Gaussian Distribution

因为我们后面会讲到如何寻找Gaussian Distribution，会涉及到非常多的Gaussian Distribution的性质，因此我们这里要回顾一下Gaussian Distribution。

Gaussian分布的通式如下

$$f_{\mu,\Sigma}(x)=\frac {1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}exp\{-\frac 1 2(x-\mu)^T\Sigma^{-1}(x-\mu)\}$$

Gaussian Distribution的表达式也是一个含参的函数，参数就是$\mu$和$\Sigma$。其中，$\mu$是均值向量，长度和feature的数量相同，而$\Sigma$是协方差矩阵，covariance matrix，是一个feature数的方阵，主对角线上的元素表示方差而其他元素表示协方差。

Gaussian Distribution这个函数的input是$x$，而对应的output是这个$x$的概率。不过严格上来说应该是概率的密度，但是我们现在说的只是单个值，因此可以理解为概率。

Gaussian Distribution给出的概率除了和$x$有关以外，还和$\mu$和$\Sigma$两个因素有关，即便是相同的$x$，不同的$\mu$或者$\Sigma$，得到的概率都不一样。下面就是几个具体的例子

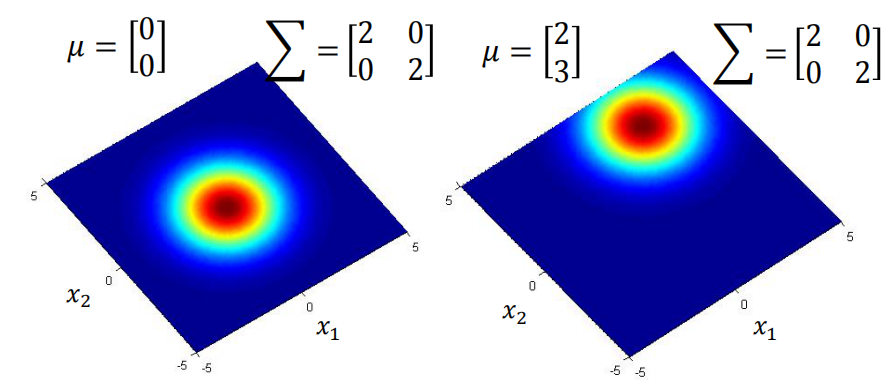
3. Maximum Likelihood

我们上面讲到Gaussian Distribution的一个性质，就是在任何地方一个具体的Gaussian Distribution（即给定了$\mu$和$\Sigma$）的值都不为0，因此从某一个Gaussian Distribution中sample得到这79个example的概率并不是0。这也就也为这，其实任意一个Gaussian Distribution都是完全有可能去sample得到这79个点的。

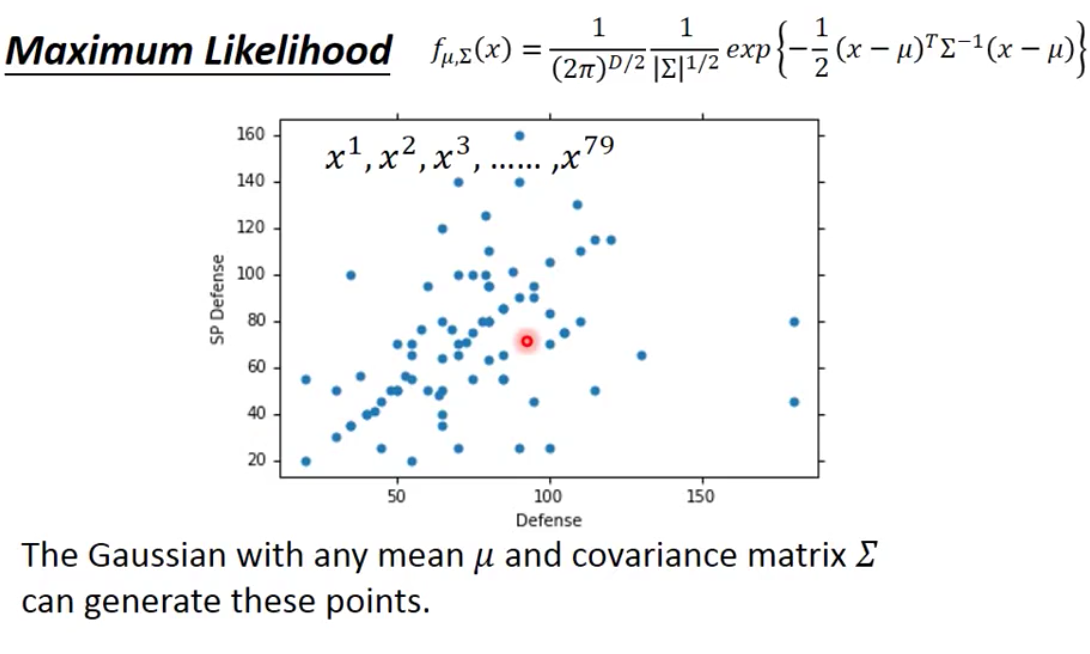
我们在图上更加形象的进行表达，左下角的Gaussian Distribution完全有可能sample得到这79个点，而右上角的Gaussian Distribution虽然不太可能得到右下角的79个点，但是概率不为0，因此还是有可能的。

然而我们上面的假设却说，这79水系神奇宝贝都是从水系神奇宝贝服从的这个Gaussian Distribution的中sample出来的。因此问题就成了：任意一个Gaussian Distribution都已可能sample得到我们这79个水系神奇宝贝，那么到底哪一个才是真真的水系神奇宝贝的Distribution呢？为此，我们就通过Maximum Likelihood来进行寻找。

上面我们虽然说任何一个Gaussian Distribution进行sample得到这79个example的概率不为0，但是每个Gaussian Distribution sample得到这79个example的可能性却不一样

例如在下图中，左下角的Gaussian就显然比右上角的Gaussian sample得到这79个example的可能性要高

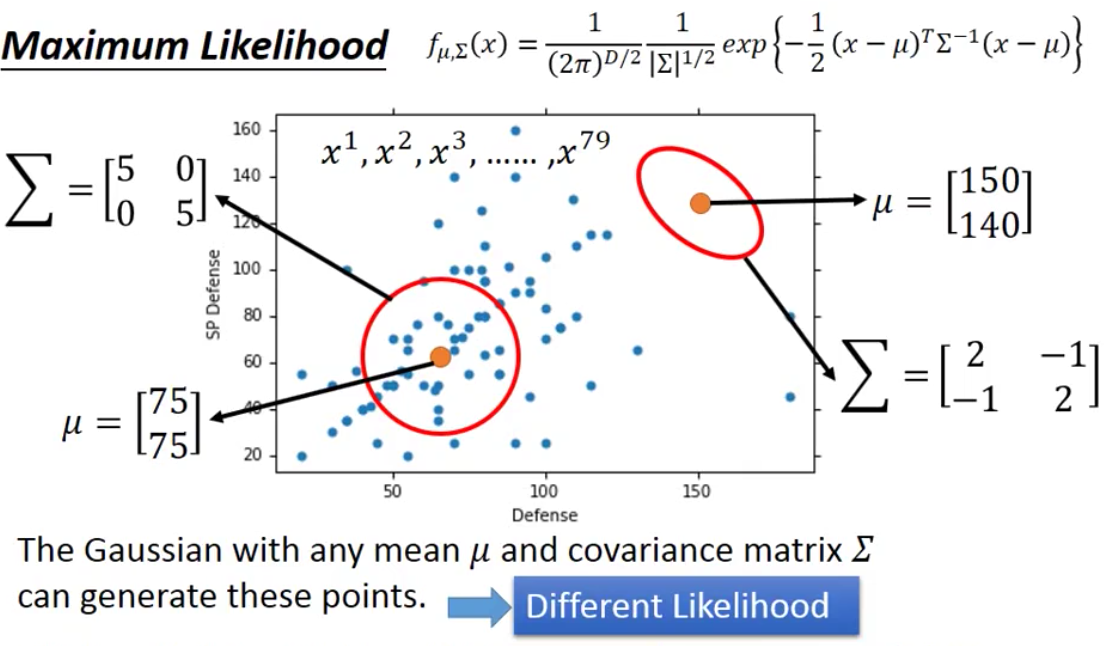
而我们衡量这个sample的可能性就是通过Likelihood（似然）实现的。

因此，当现在给定了一个Gaussian Distribution（一组$\mu$和$\Sigma$），我们就可以去计算这个Gaussian的Likelihood。因为Likelihood的开头字母也是L，这个和Loss Function撞了，但是实在是想不到更好的notation了，因此就用L来表示Likelihood。

因为我们在sample这79个example的时候都是独立进行的，因此Likelihood的计算方式就是概率连乘即可。

我们接下来要做的，就是找到能够Maximum这个Likelihood的参数$\mu$和$\Sigma$。我们记最大化Likelihood的参数$\mu$和$\Sigma$为$\mu^$和$\Sigma^$，那么形式化的表述就是

那么上面这个式子

$$\mu^*, \Sigma^*=arg\max L(\mu,\Sigma)$$

的求解，如果想爽的话当然可以自己求微分解出来。不过这个事其实已经有人帮我们干过了，我们直接套公式写出来解就行了

这个式子也是非常符合直觉的，均值向量就是每一个维度的平均，而协方差矩阵就是差的行向量和列向量相乘然后求平均

4. Pipeline

我们接下来看看上面的理论在真实的案例下的implementation。

下面是真实的水系和普通系的神奇宝贝的散点图。

然后我们用上面的理论，假设水系和普通系都有各自的分布，然后我们计算出来两个分布各自的均值和方差

然后在有了这两个Gaussian Distribution之后，我们就可以来计算$P(x|水系神奇宝贝)$和$P(x|普通系神奇宝贝)$

因此，我们就可以利用贝叶斯公式来进行分类

5. Results

我们接下来看下上面这个案例的效果。下面是两类神奇宝贝的散点图，水系神奇宝贝有蓝色的点来表示，普通系的神奇宝贝用红色来表示，$C_1$和$C_2$分别表示水系和普通系，图上的彩色线则表示相同概率的等高线。我们针对图上所有的点计算这些点是水系的概率，然后概率越高颜色就越红，反之越蓝。

其实我们肉眼就能知道估计分类效果不会太好，因为两类的分布非常的密集。

我们根据计算出来的概率，如果大于0.5则表示是水系的，小于0.5就表示不是水系的。因为我们这个是二分类，因此不是水系就是普通系。最后得到的在训练集上的表现如下

我们其实更关注在测试集上的表现，因此把测试集上的数据绘制在这个二值化的图像上，得到的结果如下

发现结果烂掉了💔。使用2个维度的值的话正确率只有47%，比瞎猜50%的表现还要烂。。。

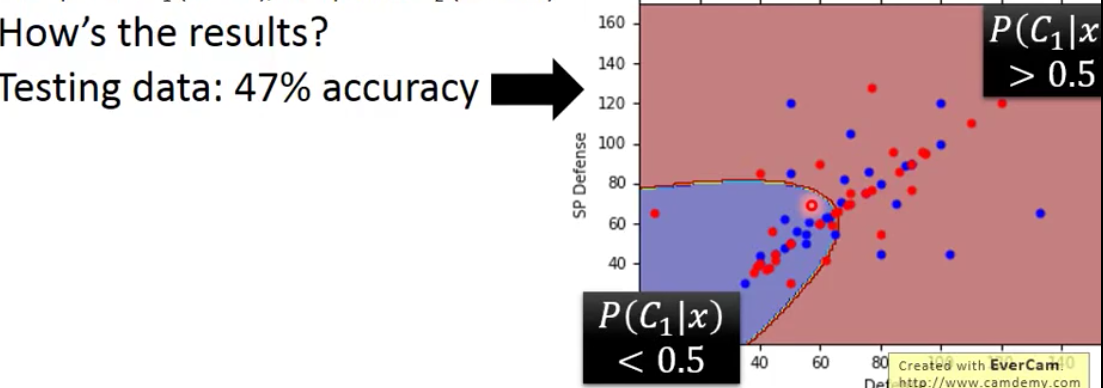
那么我们可能想机器学习厉害的地方就在于可以处理高维度的数据，因此我们就想性能烂的原因是不是因为我们只用了两个维度的数据。我们把所有的7个维度的数据用上，最后得到的结果就是在测试集上54%的准确率，之比瞎猜好一地点点。。。

6. Modifying Model

我们上面讲的模型最后的表现烂掉了，我们下面就想着能不能对模型进行一些修改，来提高模型的表现。我们根据前面的机器学习攻略手册中讲的，我们现在是在训练集上的loss小，但是在测试集上的loss大，因此我们现在的情况要么是Mismatch，要么是Overfitting。

Mismatch发生的条件比较苛刻，一般不会发生。因此我们这里其实发生的现象就是Overfitting。

而处理Overfitting要么就是增加训练的数据量，要么就是给模型进行限制。因为我们的神奇宝贝一共就这么多，因此我们只能走给模型增加限制这条路。增加限制其实就是限制模型的学习能力，为此我们需要减少参数。而减少参数的方式就是通过参数共享。

在实际的运用中，这个possibility的model大家一般都是把Variance Matrix取一样的，从而实现添加限制

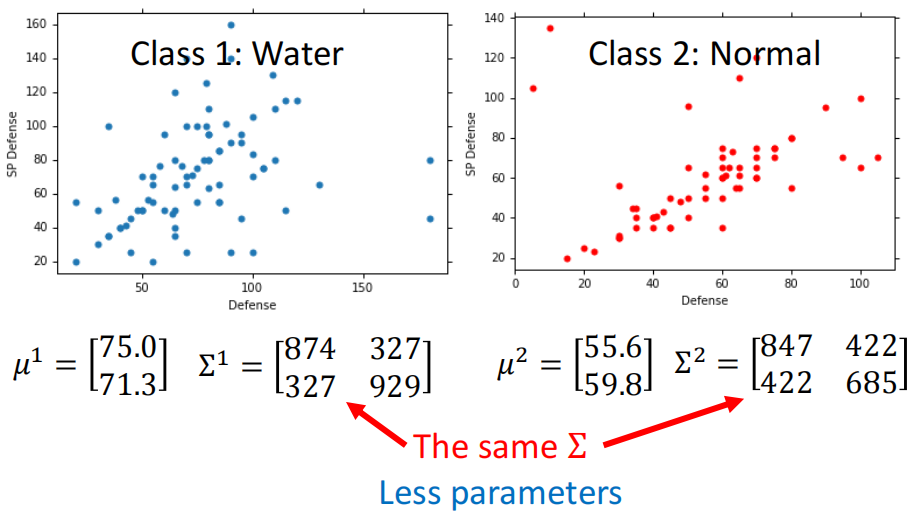
我们像上面这样添加限制，其实就等价于我们假设水系的神奇宝贝和普通系的神奇宝贝分别从两个相同covariance的Gaussian Distribution sample得到的

那么此时，我们进行Maximum Likelihood，计算均值向量和协方差矩阵的式子，就成了下面的式子

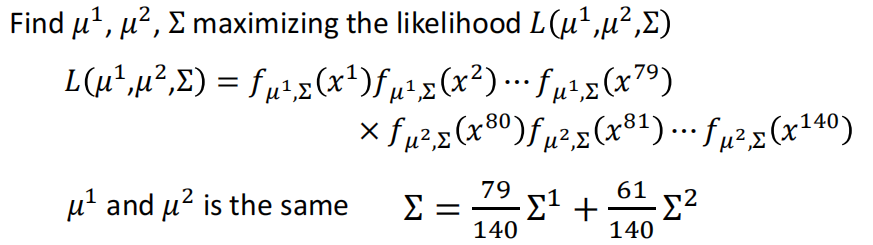
我们最后，进行修改后的模型，考虑七个维度的话，他的表现就有了极大地提升，

需要注意的是，在只有两个feature的时候，现在两个class的boundary成了线性的了。虽然我们是用概率的模型来看待的，但是因为最后的边界是线性的，因此我们也称为是一个线性的模型

7. Summary of Probability Model

我们最后对上面的概率的模型进行一个总结

机器学习的三大步：

• 定义含参的函数（模型）
• 定义衡量模型好坏的Loss Function
• Optimize得到最好的Function（最佳参数）

8. Further discussion

A. Why Gaussian

我们最后，可能想问的一个问题就是为什么我们假设的先验分布是一个Gaussian的分布而不是其他的分布。

其实关于先验分布的选择，是随意的，因为先验是我们写出的原因发生的概率，要写出来这个概率只能靠我们的认知。因此我们前面根据大数定律得到的认知就是Gaussian的分布。其实我们取别的分布也完全是OK的

不过如果我们的分布选的太简单，那么model bias可能就大了。因此具体使用那个也是看我们的。

例如我们如果某个feature的取值只有两种，表示是或者不是，那么相比于Gaussian，我们其实应该假设这个feature服从Bernoulli Distribution

B. Why high-dimension Gaussian Distribution

我们假设的Gaussian的分布是一个高维的Gaussian Distribution。那么这个其实也是我们的假设。我们完全可以假设每一个example的feature之间的取值都是independent的。换而言之每个feature都是服从一个独立的分布的。

我们假设每个feature都服从一个一维的Gaussian Distribution。这样当然也可以。这样的话其实也相当于给我们的模型添加限制。限制了covariance matrix的取值。

C. Naive Bayes Classifier

如果我们在假设每一个feature都是独立服从Gaussian Distribution的基础上，我们还假设每一个feature服从的Gaussian Distribution都是相同的。即假设每一个feature都是独立同分布的。那么这个时候，上面这个possibility model就称为naive bayes classifier

因为我们现在的假设是每一个feature都是独立同分布的，因此如果实际和我们的假设比较符合的话，那么naive bayes classifier的效果就比较，如果不是的话，那么性能就会差

4. From Probability Model to Logistic Regression

我们在最前面说道，我们这一节课的目的是为了讲解使用Neural Network进行Classification的原理。可是我们上面讲了这么多，仿佛都只讲一个新的Probability的model。看起来和Neural Network进行Classification无关

那么下面，我们就要讲解是如何从这个Probability Model一步一步的推导到Neural Network中去的

1. Posterior Probability: Logistic Regression

在概率论中，我们称某个事情发生之后，该事件由某个原因导致的概率为后验概率（Posterior）。

那么在上面的例子中，我们已经抽出来了一个圆盖海龟，它是水系的神奇宝贝这个概率就是一个后验概率，即

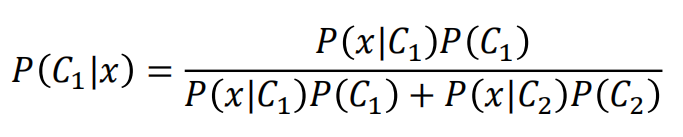
然后我们对后延上下同除分子，就得到了

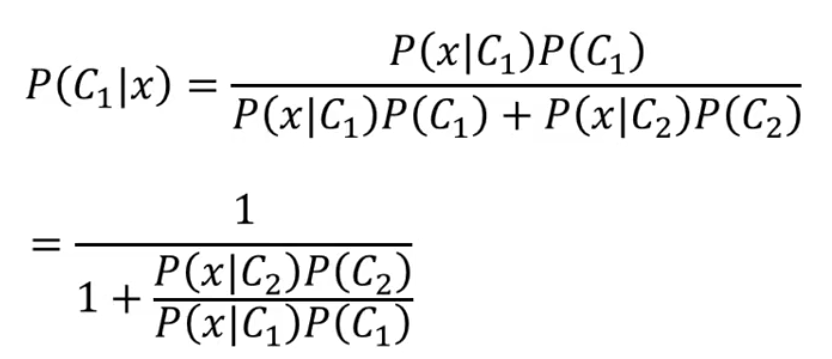
我们如果再假设

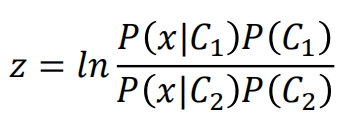
那么就得到了一个Sigmoid函数

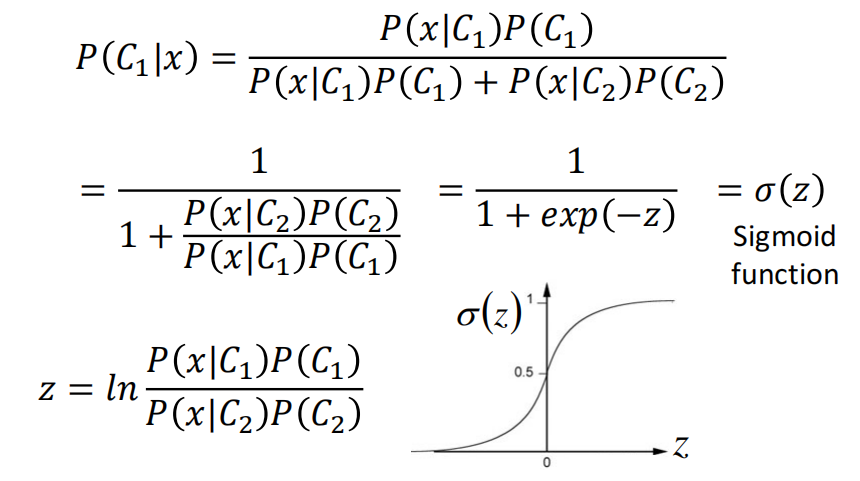
所以，到现在，我们就知道后验分布是一个变量$z$的函数

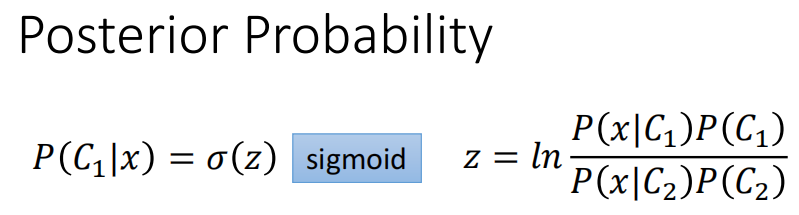
我们现在就要研究一下这个$z$到底是长什么样子的（表达式是什么样的）

我们首先把后验中的先验拆出来，那么由于我们用频率来代替先验，一次你后面的先验就可以直接表示为两类的example的比值

然后前一项我们因为假设了是Gaussian的Distribution，因此我们是可以写出来表达式的，因此我们写出来表达式，然后带进去相除

接下来我们进行化简，把指数部分相减，然后从$\ln$中取出来，就得到

然后我们就把常数项展开、合并同类项，进行化简。展开第一项的结果如下

然后把第二项继续展开，就得到了

由于我们上面假设两个Gaussian Distribution的$\Sigma^1$和$\Sigma^2$是一样的，因此我们还可以对$z$进行更进一步的化简、合并同类项

那么这个$z$其实是给$x$这个向量左乘一个矩阵，然后再加上一个向量，因此，上面的式子最终就化简为

从上面这个式子其实就能够看出来为什么边界是Linear的了。

因此，我们上面的generative的Probability的Model干的事情，其实就是我们通过一些手段，例如频率估计概率、假设高斯分布等等手段，最后算出来了$N_1,N_2,\mu_1,\mu_2,\Sigma$，然后用这些值算出来$W$和$b$。然后来来进行推断

那么我们这样是不是有一些舍近求远了，我们最重要的就是$W$和$b$，我们为什么要费这么大力气来求呢，有没有办法能够直接来求得这两个值？

这个就是我们接下来要讲的，Logistic Regression。

5. Logistic Regression

我们上面说道，Probability Model最后化简到最后就是下面的式子

$$f(z)=\frac{1}{1+e^{-z}}$$ $$z=w\cdot x+b$$

我们从概率的角度出发，假设每一类服从高斯分布，然后从training set中计算得到上式中的参数$w$和$b$。

最终判断某一个input $x$是不是$C_1$类，就是看最后得到的概率$P(C_1|x)=f(x)$是否大于0.5。

最后，我们发现Probability Model最后判断一个input $x$到底是不是属于某各类，就是根据$w,b$来进行推断，那么我们其实没有必要通过假设高斯分布、频率代替概率、通过一步步的推导最后得到参数$w$和$b$。我们就想，反正就是要这两个参数，那么我们能不能通过别的方法来获得这两个参数。那么从这个思路出发，其实就是Logistic Regression。

我们接下来就将详细的讲解Logistic Regression。

ML的三大步：

1. 定义含参函数（模型）
2. 定义损失函数（衡量模型的好坏）
3. Optimize（求解最优参数）

因此，我们下面就从这三大步出发，来介绍Logistic Regression

1. Step 1: Function Set

Logistic Regression的函数的表达式如下

$$f_{w,b}(z)=\frac{1}{1+e^{-z}}$$ $$z=w\cdot x+b=\sum_i w_ix_i +b$$

而$f_{w,b}(x)$的含义就是$x$属于某一个类的概率，即

$$f_{w,b}(x)=P_{w,b}(C_1|x)$$

我们模型里的参数就是$w$和$b$。$w,b$所有的取值构成的集合在一起，就成了我们这个模型的Function Set

我们把Logistic Regression用图形来表示出来，就是下面的图

那么现在当一个新的input $x$进入之后，Logistic Regression的计算如下

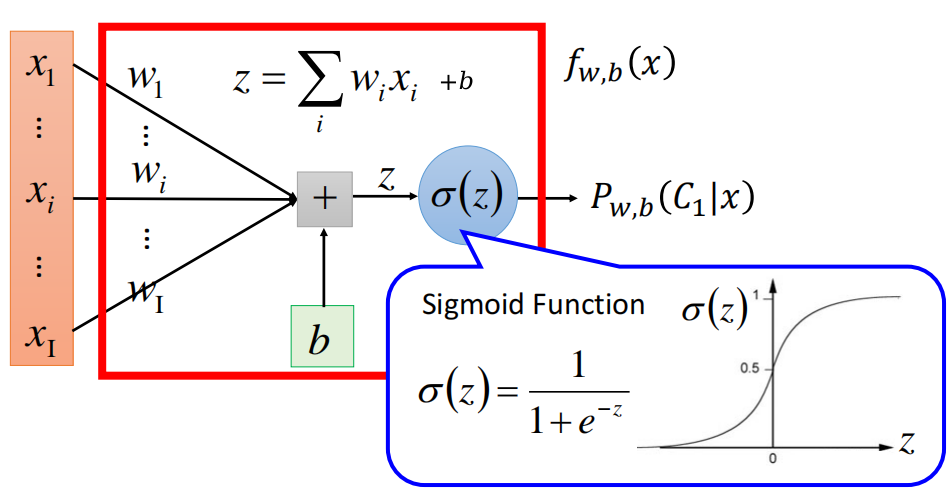
我们在最前面讲解了Linear Regression，我们和Logistic Regression进行一下比较。

Linear Regression最后没有通过Sigmoid函数，因此输出的值可能是any value，而Logistic Regression最后则因为通过了Sigmoid函数，因此输出的值只可能是介于0和1之间的值

2. Step 2: Goodness of a function

在定义完了Logistic Regression的Function Set只有，我们接下来要做的就是定义衡量模型（函数）好坏的Loss Function

我们的training set是一个input和label的pair。而label可能的取值数量和我们的类别数量一样。此外，我们还假设我们所有的数据都是从一个概率分布$f{w,b}(x)=P{w,b}(C_1|x)$生成的

模型中的参数$w$和$b$是根据某一个分布推导来的，在Probability Model中，我们假设这个分布是一个Gaussian Distribution。而带入Gaussian Distribution计算得到的结果准确的话，那么就意味着真实的data的Distribution和Gaussian Distribution长得很像。如果不准确的话，就意味着真实的data的Distribution和Gaussian Distribution差的比较大。因此我们就需要重新假设一个data的Distribution，然后带入。如果准确率较高，那么就结束，否则重新假设一个Distribution。直到我们最终找到了一个准确率比较高的Distribution。而准确率较高的Distribution就意味着它和data真实的Distribution很相近。

在表象上来说，不同的Distribution反映在模型上就是参数$w$和$b$，因此不同的$w$和$b$就表示了不同的分布。

因此，一个$w,b$的pair就和一个分布对应，因此我们衡量一个函数的好坏，就是看这个Distribution产生这些data的可能性大不大。

我们通过Likelihood来衡量这个可能性，即

注意上式中，因为我们是二分类，因此$x^3$是$C2$类的概率就是$(1-f{w,b}(x^3))$

接下来，我们再对上式进行一下数学上的变形。因为取$\ln$的话增减性不变，而在前面加了一个符号，因此maximize Likelihood就等价于minimize变形后的式子，即

​ 因为取了$\ln$，所以我们可以把Likelihood的连乘拆开

不过拆开连乘有一个很烦的事情就是，有的项是$-\ln f{w,b}(x)$，而有的项又是$-\ln(1-f{w,b}(x))$。因此我们没有办法直接写出来一个summation over n。

因此我们做一个符号上的转换，对于每一个input，如果它是class 1，他的label就是1，否则就是0。

那么这个时候，我们就可以把negative nature log的Likelihood表示为统一的式子

我们可以验证一下，发现确实是对的

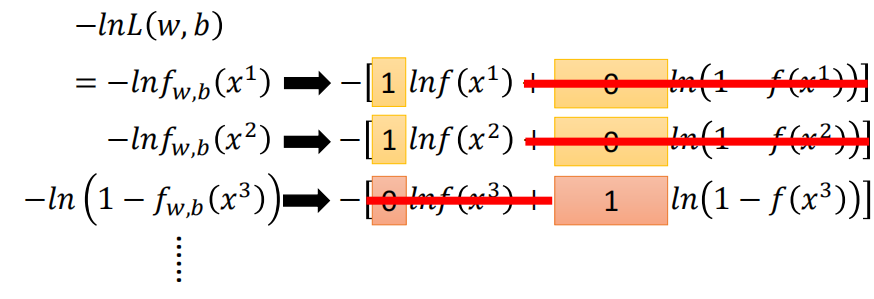
因此，我们最后就可以把负对数似然写为下面的式子

而上面的式子中，我们如果把$\hat y^n$和$1-\hat y^n$视为两个随机变量的话，那么这两个随机变量服从Bernoulli Distribution。因为我们上面假设$\hat y^n$的取值只有0或者1。

而$f_{w,b}(x)$就是描述某一个input $x$的概率，因此如果把他也视为一个分布的话，那么上面的式子就是一个交叉熵。这个时候，我们最小化交叉熵就是要让输出的分布和真实的label的分布一样

最后，我们比较一下Logistic Regression和Linear Regression在Step 2上的异同

3. Step 3: Find the best function

对于Logistic Regression来说，找到最好的Function的计算方法就是Gradient Descent。

而Logistic Regression算Gradient还是比较简单的，首先计算第一项的微分

然后求第二项的微分

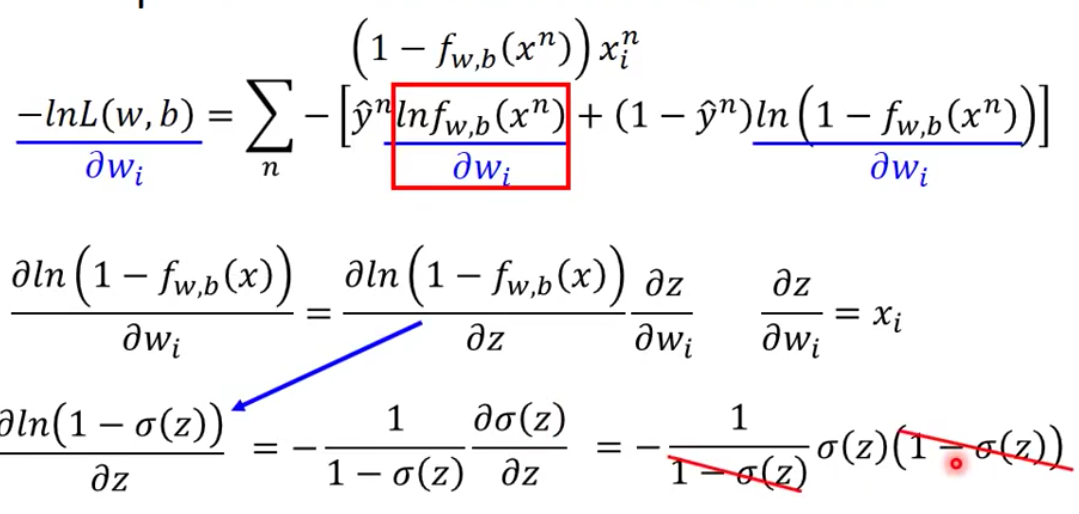
虽然中间的计算比较复杂，但是最后得到的式子很直观，就是输出和label的difference乘以input

最后，我们比较一下Logistic Regression和Linear Regression的第三步的异同，发现两者在表达式上其实是一样的。只不过是前面乘的系数的值域不同

4. Why not Mean Square Error？

我们上面在比较Logistic Regression和Linear Regression的时候，我们说道Logistic Regression的Loss Function是cross-entropy loss而Linear Regression则是使用mean square error。

造成这个现象的一个原因就是Logistic Regression我们的是从Probability的角度出发，一步步推导，最后使用Likelihood来衡量得到的。那么我们就想问为什么不能强行用MSE呢？使用MSE在这里还想也是说的通的，就是要预测的概率和真实的概率越接近越好。

所以我们不妨真实使用MSE来Train一发

那么我们使用Gradient Descent计算得到的Gradient的表达式就是上图中的最后一行。

那个这个Gradient有一个什么问题，就是在模型推断得到的概率很小或者很大的时候，不管label是1还是0，求得的梯度直接就是0了

就以两个feature的二分类来说的话，我们绘制MSE和cross-entropy的loss surface如下

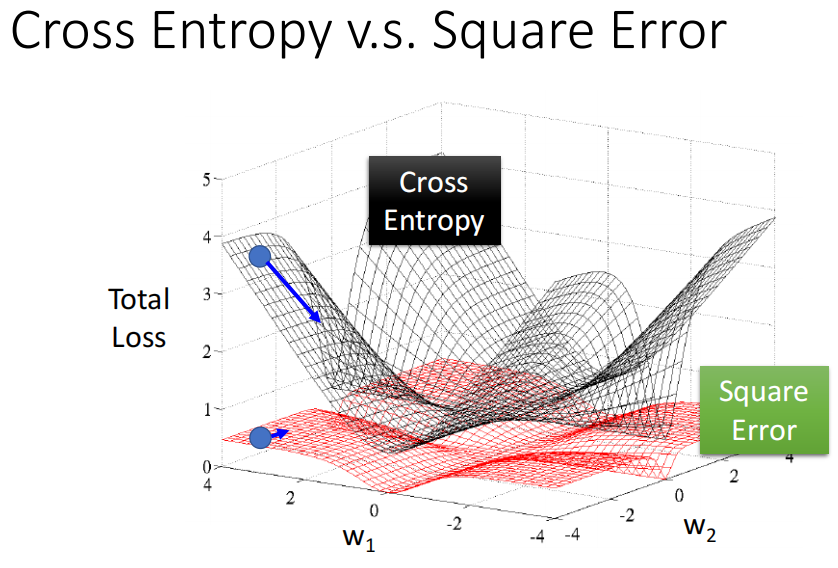
我们可以看到MSE在分类这件事情上，当距离目标很远的地方，就很平坦，对应的Gradient就是0，基本上就无法更新了。而此时cross-entropy的Gradient依然均匀，因此可以支持我们更好的进行训练。

6. Discriminative v.s. Generative

Logistic Regression这个方法我们称其为Discriminative的方法，而上面用Gaussian来描述Posterior Probability的方法称为Generative的方法。

我们下面就将比较一下两个方法的异同

1. Optimization Method

而实际上，两者Model能表示的Function Set是一模一样的，都是$P(C_1|x)=\sigma(w\cdot x+b)$，只不过两者寻找最优参数的Optimization的方法不同。

Discriminative的Model是通过Gradient Descent来求得的，而Generative的Model则是我们再假设为Gaussian Distribution的基础上求取$\mu^1,\mu^2,\Sigma^{-1}$计算得到的

而因为两个模型能表达的Function Set是一样的，因此我们就会问，Discriminative和Generative的Model两个得到的参数$w$和$b$是否是一样的

答案其实是两个方法找到的最佳的参数是不一样的，这个其实就提醒我们，尽管模型相同（意味着best function candidate是相同的），但是我们加的限制（Logistic Model中没有假设是Gaussian Distribution）不同、求解的方法不同，最终得到的参数是不同的

2. Results Comparison: Distribution in mind

我们既然说两个方法的model都是一样的，只是Optimization的方法不一样，那么我们会问哪个方法得到的结果会好一点呢？

我们看一下上面的神奇宝贝分类的例子，我们用所有的feature，最后Discriminative Model得到的准确率是79%，而Generative Model得到的准确率是73%

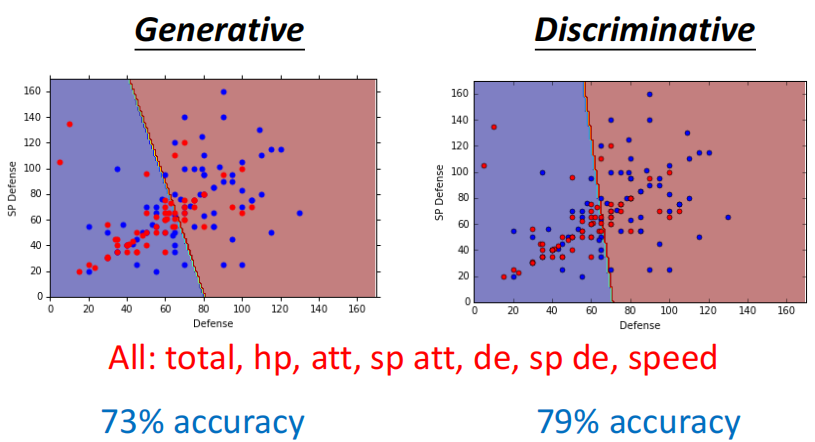
当然我们这里只有一个例子，在真实的例子中其实往往都是Discriminative的Model准确率更高。为什么会这样呢？

其实是因为Generative的Model会在心中有一个Distribution，这个心中的Distribution会影响到准确率。我们下面通过一个toy dataset讲解Distribution in mind问题。

我们假设有下面的一个dataset作为training dataset

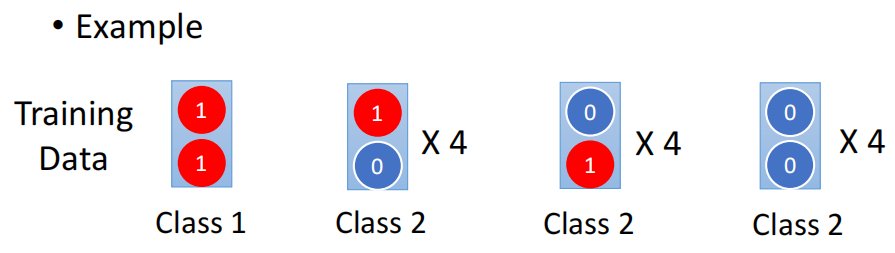
这个training data一共有13个example，其中属于class 1的example只有一个，其他12个都是class 2的example。

那么现在有一个新的input来了，我们需要判断这个input是哪一个class。我们首先用Human Learning来看一下，我们就会觉得这个input是class 1

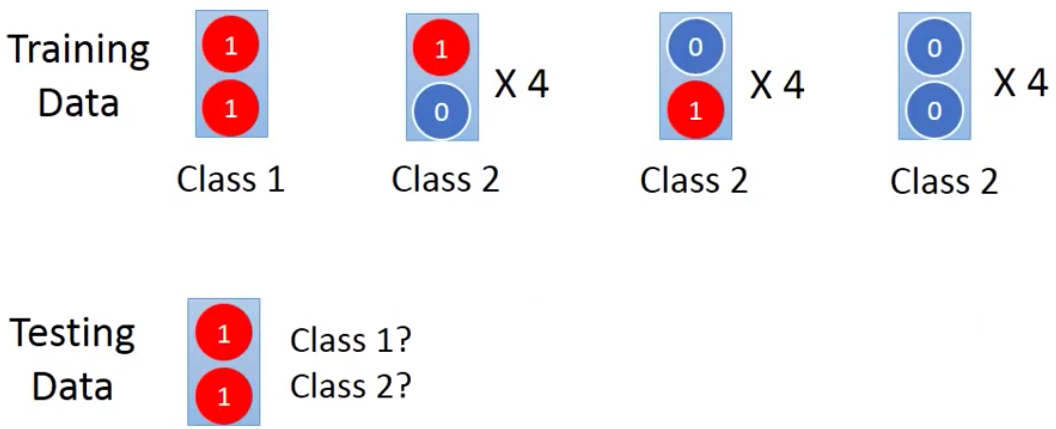
我们来看看Generative Model给出的结果。为了简单起见，我们不妨用Generative Model里的Naive Bayes

那么对于朴素贝叶斯来说，他假设input所有feature的Dimension之间都是independent的，因此一个input判断它是哪一个类，就分别判断每一个feature是不是这个类。即看所有的feature是不是都是由这个类的Distribution generate出来的。

那么我们首先计算$C_1$和$C_2$的Prior，然后在分别计算从$C_1,C_2$中sample得到$x_1,x_2$的概率

然后我们把算到的这些概率都带入到Bayesian的公式里去，计算$x$来自class 1的概率

那么我们会发现，在human看来是来自于class 1的input，在Generative Model看来它是来自于class 2的。

那么为什么会出现这样的现象呢？这是因为在我们人看来，在training set中出现了$x^1,x^2$都是1的情况，所以这个input应该就是class 1。

可是对于Naive Bayes来说，他首先不会考虑不同feature之间的correlation。因此这两个feature是independent产生的。在Naive Bayes看来，在class 2中没有看到这样的example是因为我们对真实Distribution sample的此时不够多。我们如果sample的足够多，那么搞不好会有两个feature全是1的example。

因此，Generative Model和Discriminative Model的差别就在于Generative Model做出了一些假设，首先假设data都是来自于一些分布，其次根据具体的模型的不同还有一些额外的假设。

这个假设数据都是来自于某一个分布这件事就类似于脑补，即本来不一定有这件事，你自己想象出来这件事。例如动漫里男主女主没有在一起，但是我们却想象说两个人在一起了。

因此，对于上面的Naive Bayes来说，明明在training dataset里面明明没有观察到feature全是1的、属于class 2的example出现。但是它根据心中的Distribution，脑补出来它看到了这件事情。

因此Naive Bayes会做出和人类的直觉不一样的判断。

3. Is 脑补 a good thing?

既然Generative Model会根据他心中的Distribution（我们假设的先验分布）脑补出来没有看过的example，那么我们就会问这个脑补到底是不是一件好事情？

其实脑补这件事情是有利也有弊的，优点在于：

• 因为以及假设了先验分布了，因此其实只需要用很少的数据来估计出这个先验分布的特征值，然后就可以自己generate出来其他的数据。而Discriminative Model在数据量比较少的时候，就会出现Overfitting这个现象
• 因为有了这个先验分布，因此对data中的噪声更加鲁棒
• 在Generative Model中，我们把Posterior拆成了Prior和class-dependent的概率，那么这样的好处就在于我们其实可以从不同的角度、来源来获得这个先验和class-dependent概率。例如在语音识别中，我们要识别出来一句话，然而同样的一段语音，识别出来的结果可能有很多个，那么这个时候我们其实需要的就是来获得每个识别出来的文本的概率。这个概率就是一个后验。那么我们拆成先验和class-dependent的概率之后，先验就是这句话被说出来的概率。那么要或者这个概率其实只需要从网络上爬虫爬取一下就行了。而这句话是某个class的概率（例如文本情感，那就是看从开心或者愤怒这两个class中generate出来的概率）就可以通过DNN来实现

7. Multi-class Classification

我们上面讲的全部都是二分类下的操作，在真实情况下往往都是multi-class的Classification任务。因此我们接下来讲解一下multi-class的Classification是如何操作的。

我们这里以三个class为例进行讲解，其实也可以推广到多个class的Classification上去。而且这个推广的过程和二分类非常类似。

1. Calculate possibility: Softmax

在binary的Classification中，我们判断某一个input是不是这个类，那就只需要看它的Logistic Regression的输出结果即可。如果Logistic Regression上的输出大于0.5的话，那么就是这个class，如果小于0.5的话就不是这个class，因为是二分类，不是这个class就是另外一个class。而之所以要大于0.5的话，是因为Logistic Regression的输出是属于这个类的possibility。

而在multi-class的 Classification中，由于当这个class的概率小于0.5的时候还有两个class候选，因此其实没办法只用一个Logistic Regression来完成。因此使用Logistic函数得到的输出就不再是possibility了

为此我们用一个Logistic Regression的加强版，即使用一个softmax来得到概率，而此时因为是多分类，所以我们是选择概率最高的类作为Classification的结果。

下面我们就讲讲softmax计算的方法。

首先对于softmax来说，每个class都有一组参数$w^i,b_i$，这样的话，先让一个input通过三组$w^i,b_i$，就得到了三个$z_i$。

在Logistic Regression中，我们最后是通过Logistic函数来实现将值转换为概率。而这个值则是与某一个input和Distribution对应。我们推导Logistic函数的时候是通过二分类的贝叶斯公式。

那么类比于二分类的贝叶斯公式，我们对多个class（原因）的贝叶斯公式写出来，然后除以分子的话，就得到了softmax函数。

因此，在计算得到三个$z_i$之后，我们接下来用softmax实现从值转换为概率。

softmax具体的计算的图示如下

即首先计算三个z的exponential，然后求和再除三个z的exponential，这样就得到了最终输出的概率。

我们举一个具体的例子，假如说现在计算得到的三个值是-3、1、3，带入之后计算的概率分别是0.88，0.12和约等于0。所以我们就说这个input $x$在分类的结果就是class 1

在通过softmax之后得到的是概率，因此最终输出的所有值均满足：求和为1，各自在0-1之间这个特点

2. Loss Function

在binary的Classification中，计算Logistic Regression的参数好坏的Loss Function是cross-entropy，而推到得到cross-entropy是通过Maximum Likelihood得到的。

这个过程完全可以扩展到多个类上去。因此，multi-class的Logistic Regression的损失函数也是使用的交叉熵，其具体的计算如下

考虑到我们的target都是one-hot向量，因此其实计算完Cross-Entropy之后得到的possibility名义上是三项的summation，其实只有一项。而在求梯度反向传播的时候，则在softmax这一层从一个Gradient传播到了三个方向去。因为softmax计算的时候有用到三个feature计算exponential的summation。

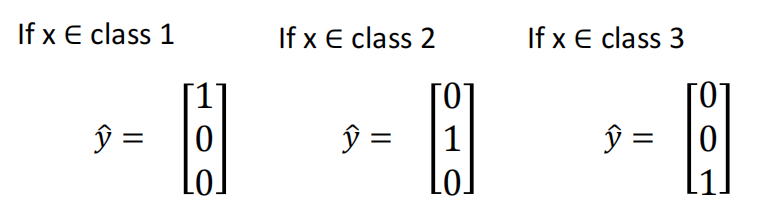
8. From Logistic Regression to Neural Network

1. Limitation of Logistic Regression

实际上我们说Logistic Regression并不是万能的，而是有缺点的。例如下面的例子，我们现在的training data只有4个example。

我们现在就是要让Logistic Regression对这四个example进行二分类，即希望对class 1的两个example通过Logistic Regression后计算出来的概率大于0.5。

那么我们其实会发现，这件事其实是办不到的。因为对于Logistic Regression来说，他计算得到的boundary其实是一条直线，因此不管我们怎样的画这条直线，都是没有办法完成这个分类的

2. feature transformation

为了解决上面这个Logistic Regression的limitation，我们可以通过特征变换来实现。我们想想我们之所以无法用Logistic Regression分出来的结果是因为我们的feature选的不好。因此我们可以先对feature进行变换，得到一个良好的feature之后就可以让Logistic Regression完成分类了。

举例来说，上面的例子中，我们原有的feature space中Logistic Regression是无法完成分类的

那么我们可以通过现有的feature来构造（transform）新的feature，例如我们这里构造出来新的feature $x_1’$和$x_2’$分别表示原来的点到$(0,0)$和$(1,1)$的距离。这样的话，Logistic Regression画一条线出来就可以实现分类

然而有一个问题就是这个feature transformation我们其实并不是每次都知道怎么做，或者说并不是所有的feature transform都是像我们这里进行的transform一样简单

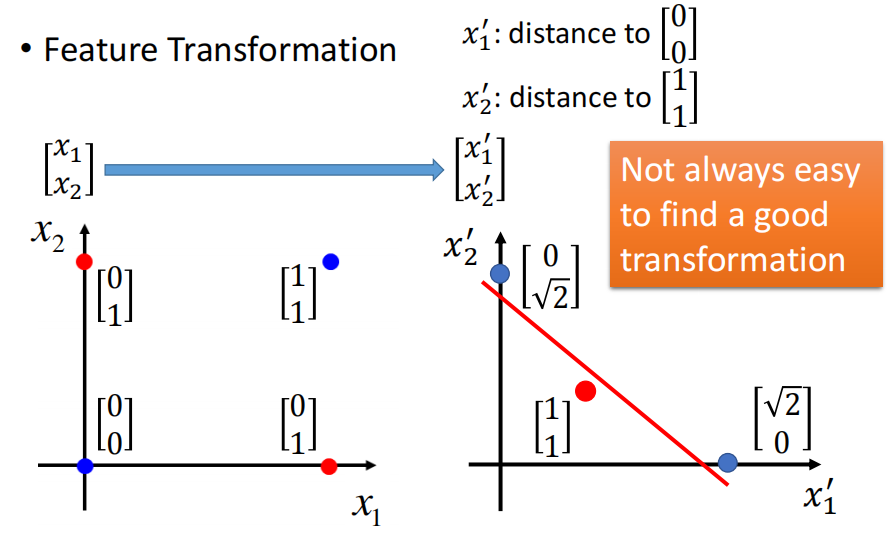
而我们如果花费太多的时间在寻找transformation的话，那么其实就不是机器学习了，反而是人的智慧了。因此相比于我们handcrafte出来这个transformation，我们更希望能够让机器去自己学到这个transformation

3. Cascading logistic regression models

我们如何实现让机器自己去学习到这个transformation呢？其实只需要把多个Logistic Regression的model cascade起来就行了

因为进行变换其实就相当于乘以一个矩阵进行基座标变换，而我们套上Logistic Regression把这个值放缩到0-1区间内。那么这样最后得到的输出我们就可以认为是新的feature

那么这样，在机器学习的时候（Gradient Descent的时候），其实就会学习前面参数$w{11},w{12},w{21},w{22}$。也就意味着，机器自己学习这个transformation。最后再接一个Logistic Regression进行分类即可

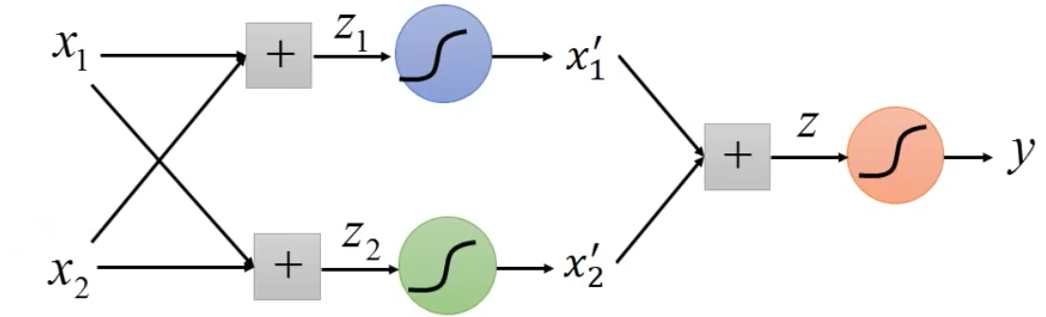
因此，我们这个cascade Logistic Regression中，三个Logistic Regression中前两个用于feature transformation，一个用于Classification

4. Cascade Logistic Regression to Neural Network

每一个Logistic Regression的input可以有多个数值，因此我们其实可以把多个Logistic Regression以一个复杂的形式连接起来。

然后称每一个Logistic Regression的unit为一个Neuron，然后很多个Neural 连接起来就是Neural Network。

更进一步，既然前面是在transformation，那么其实没有必要要通过Logistic函数，我们可以给前面的feature transformation的地方通过relu等其他函数，只需要保持最后分类的地方的Logistic或者softmax函数不变即可。

这样的话就最终成为了我们标准的使用神经网络进行分类的模型。

9. Summary

最后，我们进行一下总结。我们本节课的目的在于配合前面讲解神经网络分类的short version版本，我们完完整整的从Probability Model出发，一步步讲解，然后引出Logistic函数背后的意义是概率。进一步从概率的角度出发，讲解使用cross-entropy背后的原理是交叉熵。最后讲解多分类的时候使用softmax其实就是Logistic的二分类的贝叶斯公式的多分类推广。

我们为了讲解上面这段话，让其中的每一段都rationale，我们绕了不少弯路，特地的讲解完了Probability Model和Logistic Regression。

不过我却认为这些弯路并不是白费的，因为我们更加深刻了理解了分类为什么是使用softmax以及使用cross-entropy的原理。

16414个字，目前为止最长的文章了，辛苦我自己了~

继续加油🐛🐛🐛