本文是Machine Learning 2021 Spring 第五节课的笔记,本节课主要讲解了如何利用深度学习进行分类。

李宏毅ML2021-Spring-5: Classification (Short Version)
在前面的课程中,我们在第二节课:Introduction of Machine/Deep Learning的时候就首先介绍了机器学习就是找一个函数,然后根据要找的函数的不同,机器学习的任务可以分为三种:
- Regression:机器需要寻找的函数的输出是一个(连续的)数值
- Classification:机器的输出是多个选项中正确的一个(类别) ,这些选项都是人类提前给定的
- Structured Learning:略
我们在这些课中还通过YouTube观看人数预测这个任务,从Linear Model出发,从函数拟合的角度慢慢引入到Deep Learning。最后我们讲解了如何用Neural Network来解决YouTube观看人数预测这个任务。
那么其实YouTube人数预测这个问题中,它的输出人数就是一个连续的数字,因此其实那里的Neural Network解决的就是一个Regression的问题。而让网络解决Regression问题其实也很简单,就是让网络最后输出一个数值就行了,非常的简单。因此我们没有专门的讲解Regression问题。
对于Classification来说,因为要做选择,所以最后到底该怎么样的改变网络才能让网络输出一个选项呢?本节课将讲解Neural Network如何解决Classification任务
1. Short Version
在以往的课程中,关于如何使用深度学习来进行分类这节课会讲一个小时左右,但是因为今年这次课时间有限,所以会讲一个短版本的如何使用深度学习来进行分类。
具体来说,这个短版本会直接告诉你通过深度学习来进行分类的操作,更多的intuitive和insight都省略不讲,如果想学习的话得自己去看往年的课程。

1. About Notations
在机器学习中,关于符号其实是没有统一的规定的。有的人用$(x,y)$表示example,用$\hat y$表示模型的输出,也有的人从函数的角度出发,将$y$定义为模型的输出,而$x$是input的example的feature,真实的label用$\hat y$来表示
本课程中,老师就是从第二个观点出发做给出的记号

2. Classification as Regression
我们在前面讲了如何用神经网络来解决Regression问题。那么我们首先想,能不能让网络把分类问题当做一个回归问题来处理。具体来说就是我们现在把每个class和一个数字绑定。
然后我们训练的时候还是用MSE如果RMSE这样的损失函数让网络的输出越接近代表这个类的数字就行了

但是这样做其实是有问题的,因为我们这样做,其实暗含了这样的假设:Class 1和Class 2更加相似,而Class 1 和 Class 3会比较不同。因此,这样做其实人为的引入了相似性
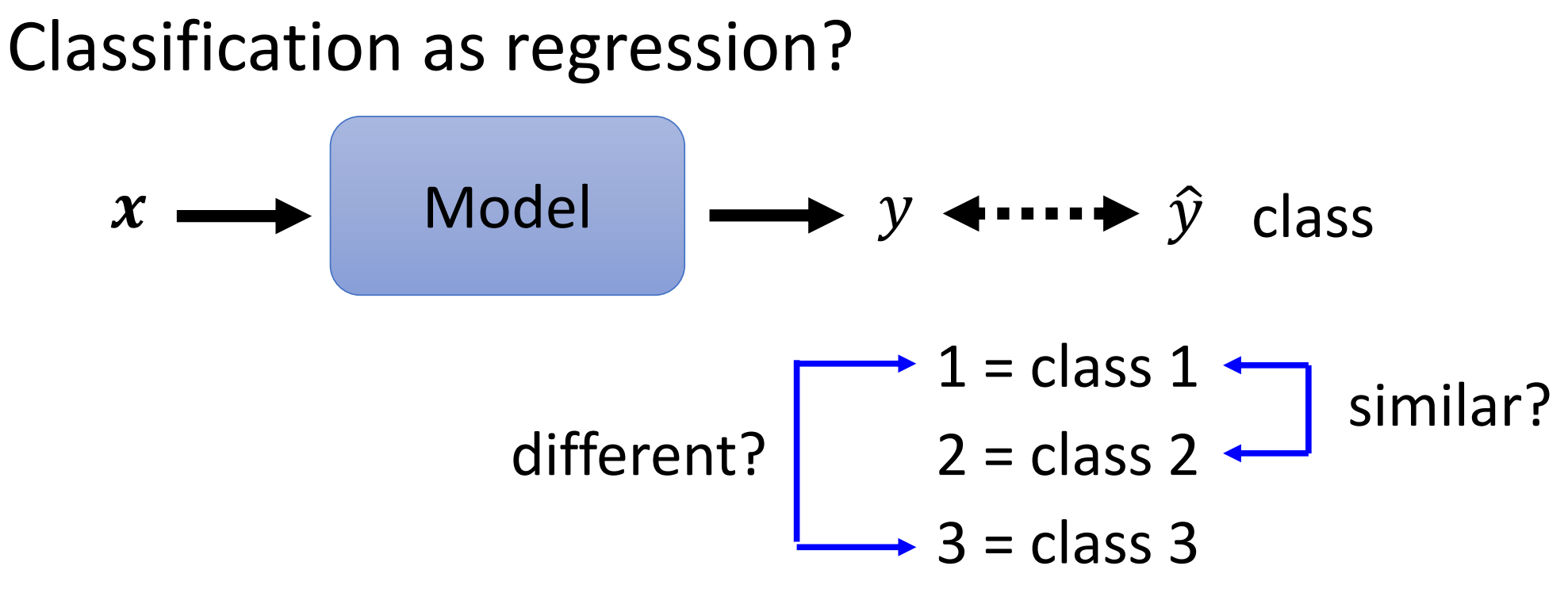
在有一些场景下,不同的class之前确实是有关系的,比如根据小学生的身高体重来判断这个学生是几年级的学生。那么一年级和二年级之前确实比一年级和三年级之间更加相似。因此这个时候这样去用Regression来解决Classification问题是OK的。
可是在很多情况下,不同的class之间是没有关系的,比如进行水果、汽车等几类物体的划分时候,不用的物体之间其实并没有特别的关系,因此这个时候给不同的类之间加上这个关系就会显得不是很正确
3. Class as one-hot vector
那么其实在做分类的时候,更常见的做法是用one-hot vector来表示不同的类。
假设我们有三个类,那么我们就用一个长度为3的向量来表示这三个类,每一个维度上如果是这个类就是1,如果不是这个类就是0
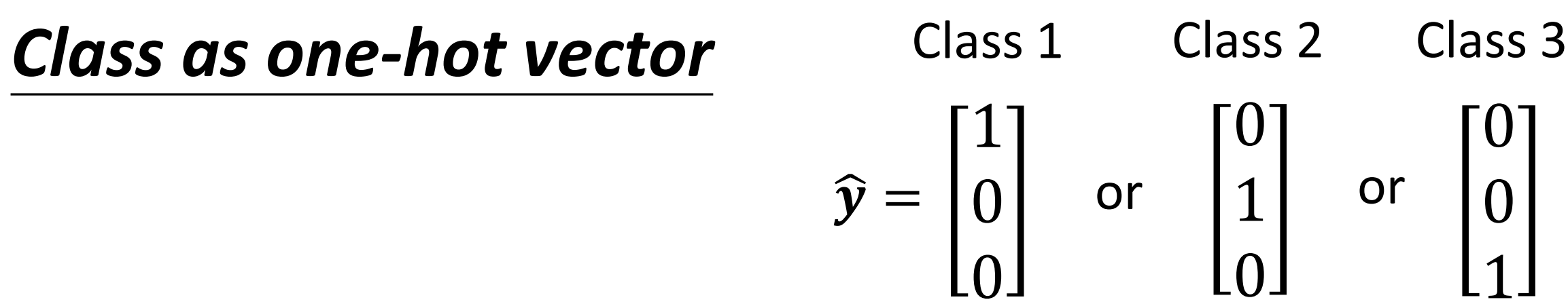
那么现在有一个问题就是,我们的网络给出的输出都是一个数字,然而现在label变成了一个向量。可是我们的Label却是一个三维的向量。

因此我们现在还需要对网络的结构进行修改,让它重复输出三个数字,也就是分别乘以三组不同的权重,最后就能够输出三个数字。所以修改其实也很简单,就是把Regression的输出层按照上面说的修改一下即可

所以我们现在给一个input(这里input)是有三个feature,然后期待网络输出的向量$(y_1,y_2,y_3)$和他真实的类越接近越好
4. Softmax
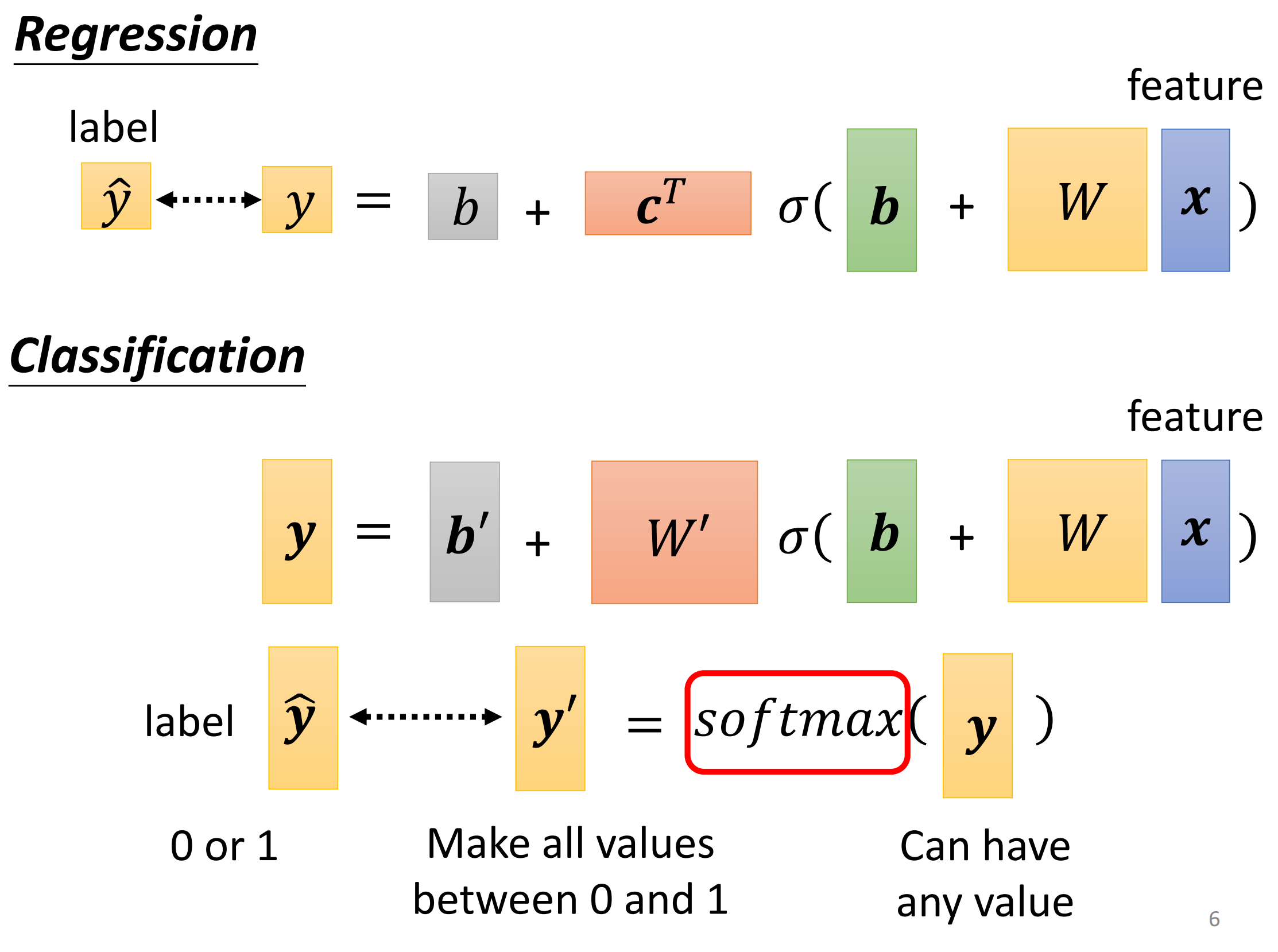
我们网络现在能够根据输入给出一个输出向量,但是和Regression不同的是,Regression最后直接用这个输出的值当做预测的值即可,而Classification其实不能直接用这个输出来直接作为预测。
一个原因就是我们输出的y的范围其实是从正无穷到负无穷的即$y$其实可以是任何值,而在我们上面的one-hot vector中,我们则是要求每个example的label的$\hat y$的值要么为0要么为1,因此在直接给出预测前还需要进行一步操作。
我们通过softmax把最终输出的$y$的值不改变相对大小放缩到0~1之间。
当前,上面这个所谓范围的这个解释只是骗小孩的,在他背后有更深层次的原因,不过在这里我们不进行深入的讲解,如果有需要的话得自己去看往年的长版本的课程。
而softmax具体的计算过程如下,首先对每个$y$去exponential,然后再做归一化
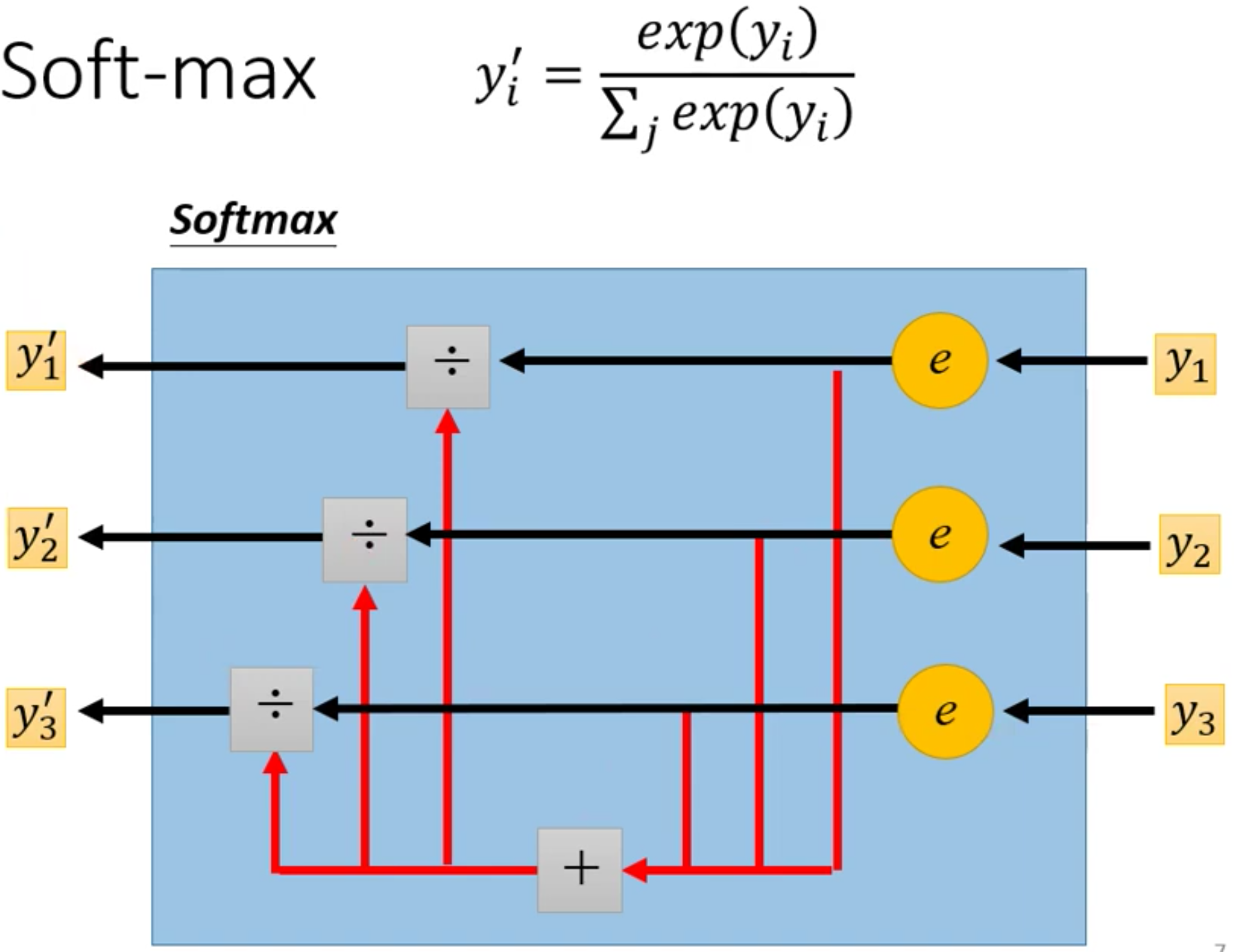
而Softmax的特点有两个:
- 所有的值都是介于0~1之间的
- 所有的值的和是1
- 大的值和小的值差距更大
下面是一个Softmax的计算的例子,我们通常把softmax的输入称为Logit
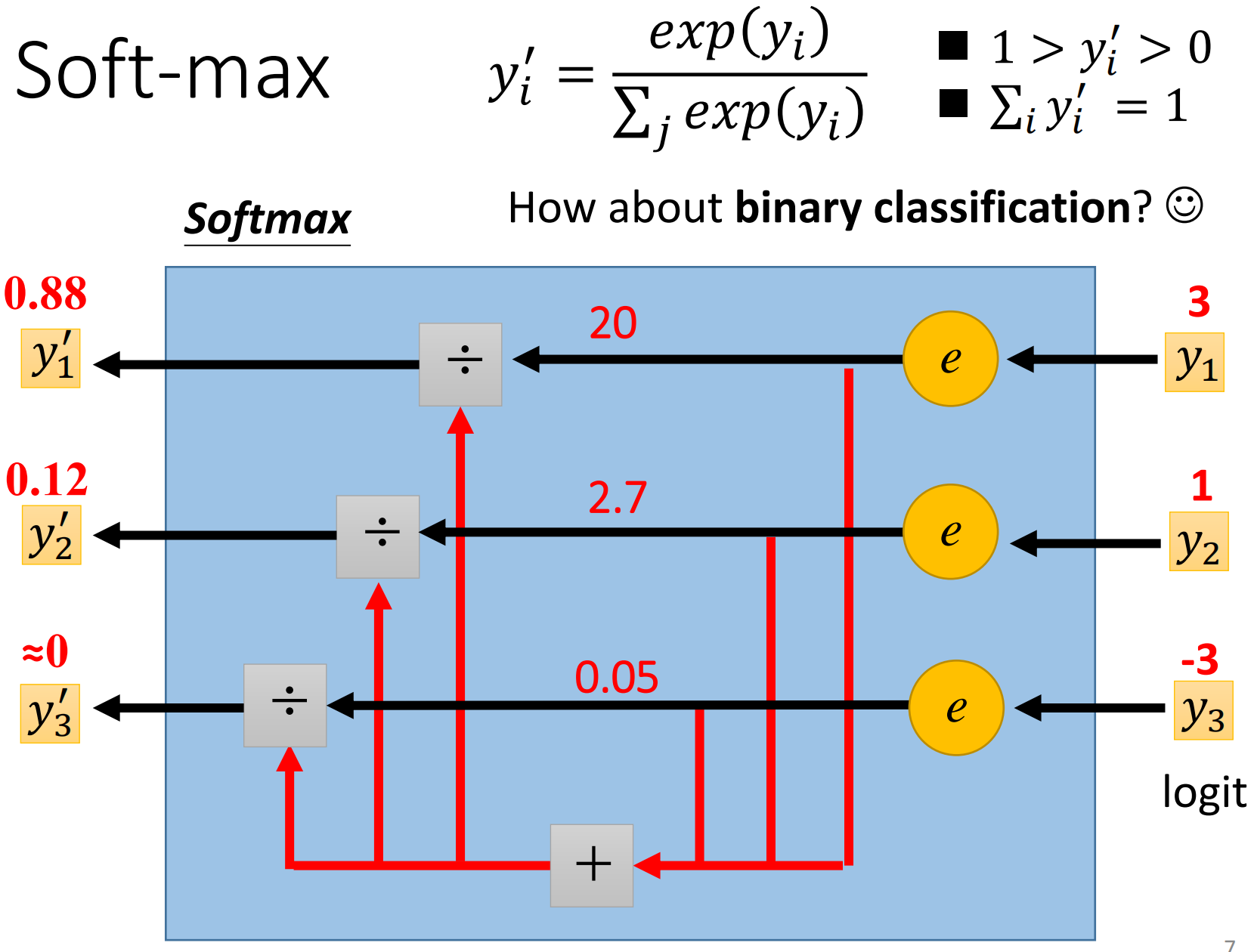
最后,对二分类来说的话,我们其实用Sigmoid就行,因为这个时候Sigmoid和softmax是等价的
5. Loss Function of Classification
我们在定义了模型只有,接下来的一步就是要确定损失函数用什么。在Regression中我们直接用MSE计算得到的距离来衡量即可。
在Classification中我们当然也可以用MSE作为损失函数
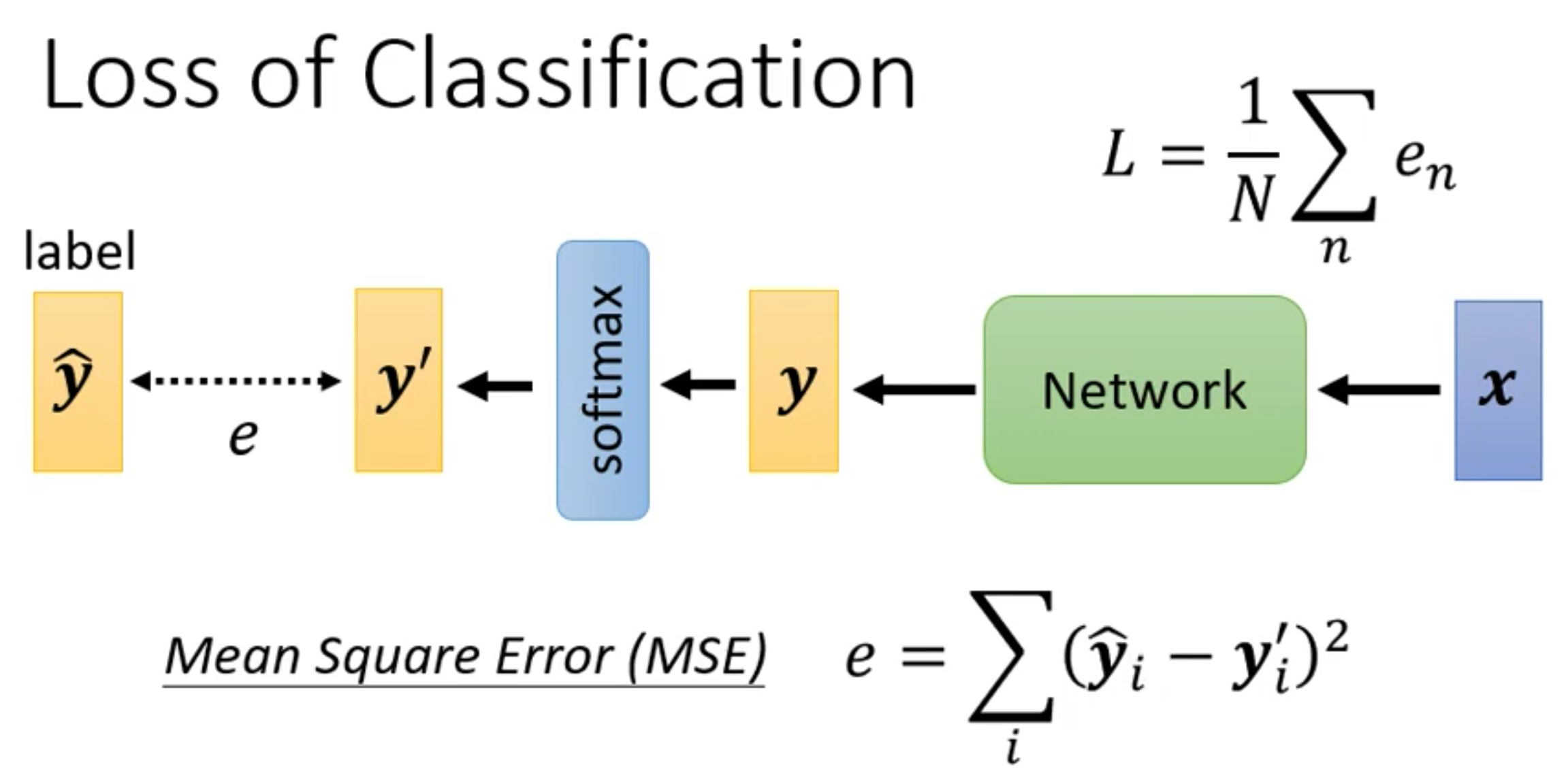
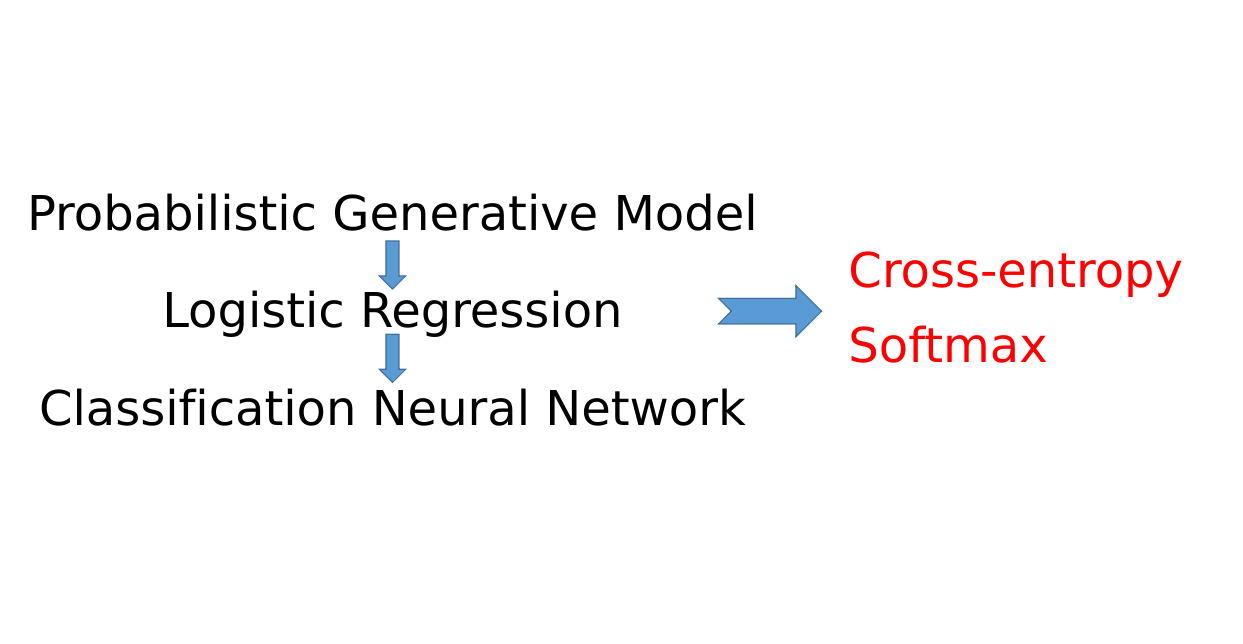
然而在Classification中,其实更常用的损失函数是Cross-Entropy
而交叉熵损失的表达式如下,summation of all i, yi hat dots yi prime natural log。
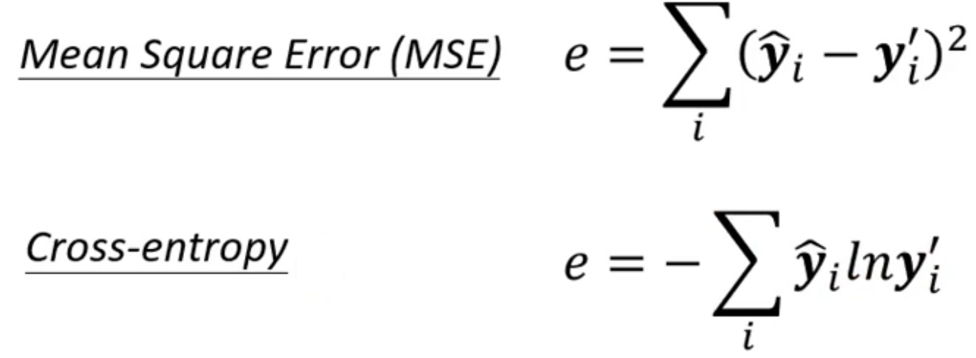
那么为什么要minimize cross-entropy,其实我们也不讲,这个原因(故事)得去长版本的讲解里听。
不过这里简单的说一下,minimize cross-entropy就等价于maximize likelihood

而对于分类任务来说,cross-entropy实在是太常用了,因此在Pytorch里面,softmax是和cross-entropy绑定在一起的,我们只需要调用cross-entropy就会自动的先计算softmax
下面我们从一个例子来讲解为什么cross-entropy要比mse要好。
假设我们现在做一个三分类的任务,下面是我们的模型图

我们现在假设$y_1$和$y_2$分别从-10-10变化,而$y_3$固定取-1000
那么我们就得到了下面的Error Surface
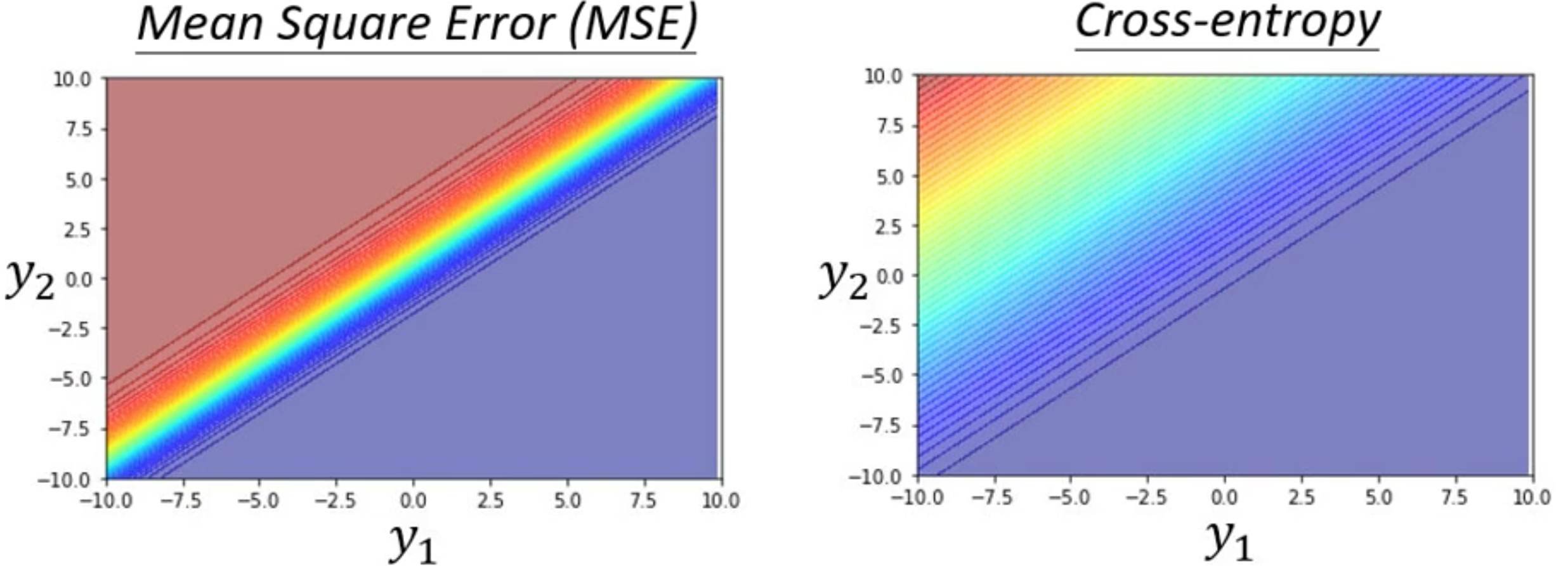
那么能看到,在两种损失函数的曲面上,越靠进右下角损失就月小,而右下角就表示$y_1$很大而$y_2$很小,其实就表示预测的类别是$y_2$
同理,左上角loss大是因为直接预测错了。
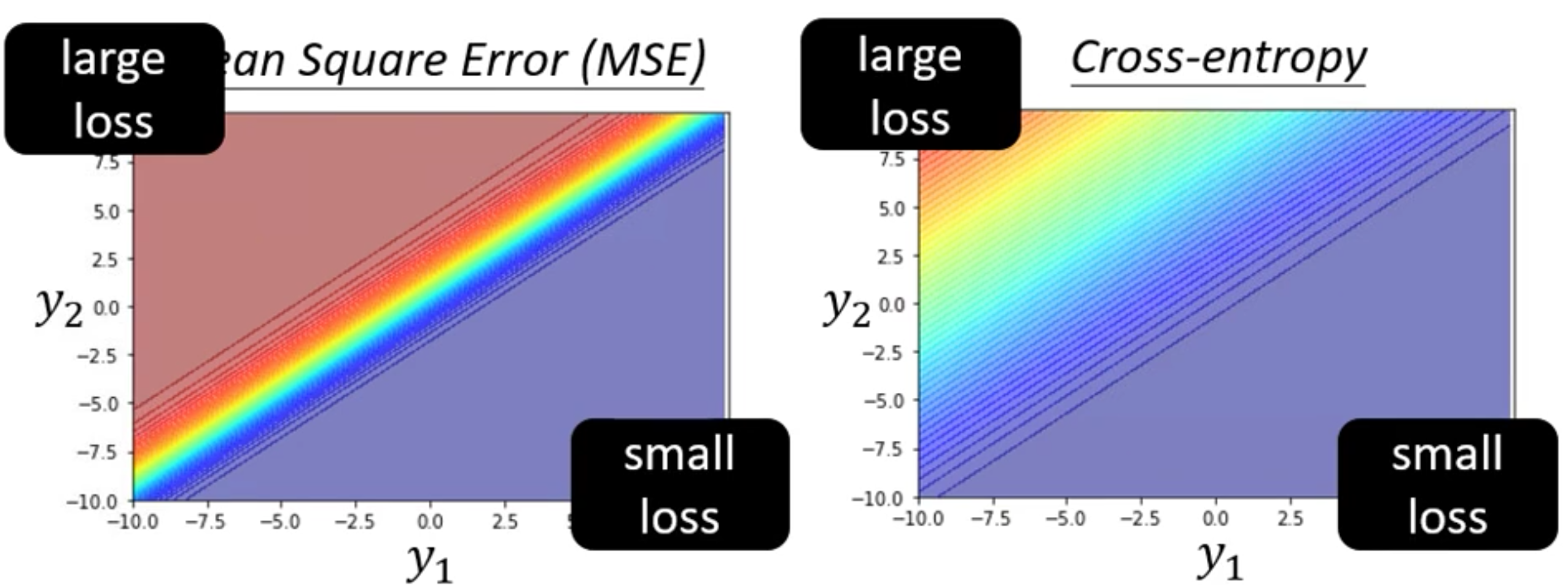
那么假如说我们现在起点都在左上角,那么其实左边使用mse的话,是没有斜率的,因此就无法更新,而右边的使用cross-entropy则是因为有斜率,所以可以到达右下角。所以针对与分类任务来说,使用Cross-Entropy会更好

最后,上面这个例子其实给了我们一个启发,就是我们针对不同的任务要使用不同的损失函数。