本文主要讲解了数学建模的题型划分、常用算法分类以及常用算法的适用场景

数学建模备赛：数学建模题型划分、常用算法分类及其适用场景

一、数学建模常见的赛题类型

数学建模常见的赛题类型一般可以分为四种：

• 优化类
• 机理分析类
• 评价类
• 预测类

严格来说，数学建模比赛的赛题变化莫测，上到卫星变轨，下到捕鱼摸虾应有尽有，虽然题目各种各样，但经过分析探究发现主要集 中在上面这四大类，其中

• 优化类赛题是考察的最多的，不管是美赛还是国赛，每年都会有题目涉及优化问题，如国赛2016B：风电场运行状况分析、2015B：出租车资源合理配 置等
• 其次是机理分析类，如2016B：小区开放对道路通行的影响分 析、2011A：城市表层土壤重金属污染分析等
• 评价和预测类赛题由于解题较为简单，出的相对不多。

具体对于美赛来说，数模美赛MCM和ICM各自有三道题，然而这六道题的每一小问其实都可以划归为上面的四类问题。

A. 预测类问题

所谓的预测类问题，指的是通过分析已有数据或现象，找出其 内在发展规律，然后对未来情形做出预测的过程。

例如：

• 国赛2007A：中国人口增长预测问题
• 国赛2016C：电池 剩余放电时间预测等
• 美赛2013ICM：地球健康的网络模型

而根据已知条件和求解目的，往往将预测类问题分为：

• 小样本内部预测
• 大样本内部预测
• 小样本未来预测
• 大样本随机因素
• 周期特征的未来预测
• 大样本的未来预测

此外，预测类问题可以是以一个大题的形式出现，也可以是以一个大题中的某一小问的形式出现。但是，预测问题主要是以某个 小问的形式出现，很少有整个赛题所有小问全是预测要求的

B. 评价类问题

所谓的评价类问题，指的是按照一定的标准对事物的发展或现状进行划分的过程。在数学建模中出题点可体现在对生态环境、社会建设、方案策略等进行评价。

评价类赛题往往没有明确的指标体系和评价标准，往往是需要同学们查阅各类资料进行构建的，因此评价类赛题也没有明确的答案。 过去的评价类问题：

• 2010国赛B题：2010年上海世博会影响力的定量评估
• 2012国赛A题： 葡萄酒的评价
• 2014年美赛MCM B题：大学运动教练挑选

注意：评价类问题近些年在美赛赛题中频繁出现。解决评价类赛题的关键是指标体系的构建，构建完评价体系后在选择合适的评价方法即可，体系建立应秉持全面、准确、 独立的三要素

C. 机理分析类

所机理分析是根据对现实对象特性的认识，分析其因果关系， 找出反映内部机理的规律。

1. 在求解机理分析类问题时首先需要探寻与问题相关的物理、化学、经济等相关的知识
2. 然后通过对已知数据或现象的分析对事物的内在规律做出必要的假设
3. 最后通过构建合适的方程或关系式对其内在规律进行数值表达。

机理分析在国赛美赛中的出题点较多，如:

• 2014年国赛A题：嫦娥三号软着陆轨道设计与控制策略
• 2016国赛B题：小区开放对道路通行的影响
• 2013美赛MCM(A)：车辆右行问题

机理分析立足于建立事物内部的规律，相对于其他类型的赛题均有章可循。机理分析类赛题往往需要结合众多关联知识才可以进行求解，如空气动力学、流体力学、 热力学等

D. 优化类问题

优化类问题时数学建模中最为常见的赛题，所谓的优化指在现有条件固定的情况下，如何使目标效果达到最佳。如在一座城市公交车公司拥有的公交车数量是固定的，问如何安排线路能够使盈利达到最高

优化类问题往往需要分析三个关键因素： 目标函数、决策变量和约束条件，三者往往缺一不可。不管是国赛还是美赛，对于优化类赛题每年都会出，如：

• 2019年国赛C 题：机场的出租车问题
• 2020国赛C题：中小微企业的信贷决策
• 2020年美赛E题：淹死在塑料的海洋中

优化类问题是当前美赛最常见的赛题，解决优化类赛题必须知道优化的目的、约束的条件和所求解的关键变量，需要有较强的编程能力和赛题分析挖掘能力

二、数学建模算法体系分类

数学建模中的算法大致可以分为下面的几类：

• 数据预处理模型
• 优化模型
• 预测模型
• 评价模型
• 聚类分析模型

每类模型中又会有很多的算法，常见算法的分类如下

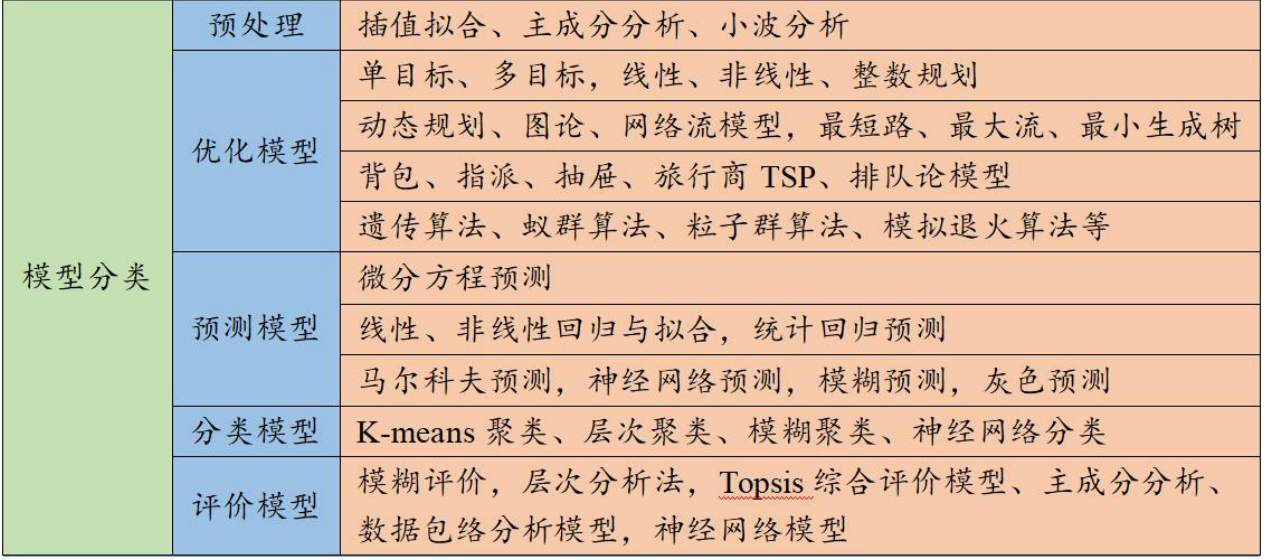
上面的这些算法都是基础的算法，因此要全部掌握。

而在实际比赛的时候是不限制模型的使用的，以实用为准，而每种模型均有其实用的场景，因此切勿盲目追逐较为复杂繁琐的模型。

下面就将讲解各类模型及其运用场景

A. 数据预处理模型及应用场景

1) 插值拟合

• 主要用于对数据的补全处理
• 其中样本点较少时（泛指样本点小于30个）采用插值方法，主要有拉格朗日插值算法、牛顿插值、双线性内插和双三次插值
• 当样本点较多时（泛指样本点大于30个）则采用拟合函数，即考虑随机误差

2) 小波分析，聚类分析（高斯混合聚类，K-均值聚类等等）

• 主要用于分析诊断数据异常值并进行剔除
• 小波分析：适用于时域范围的大样本异常值监测
• 聚类分析：适用于空间分布的大样本/小样本异常值监测

3) 主成分分析、线性判别分析、局部保留投影

• 主要用于多维数据的降维处理，减少数据冗余等

4) 均值、方差分析、协方差分析等统计方法

• 主要用于数据的截取或者特征选择等

B. 优化类模型及应用场景

优化问题的三要素：

• 决策变量：通过变量的改变，获得更好的结果。 它可以理解为控制变量，或者是一些决定性的参数。
• 目标函数：评价是否向着好的方向发展，用来评测的标准。
• 约束：它限定了决策变量的具体的设置范围一个定义域限定。

1) 单目标优化

• 所评测目标只有一个，只需要根据具体的满足函数条件， 求得最值
• 适用场景：针对问题所建立的优化目标函数有且仅有一个

2) 多目标优化

• 多个评测函数的存在，而且使用不同的评测函数的解，也是不同的。也即是说：多目标优化问题中，同时存在多个最大化或是最小化 的目标函数，并且，这些目标函数并不是相互独立的，也不是相互和谐融洽 的，他们之间会存在或多或少的冲突，使得不能同时满足所有的目标函数。例如金融投资中，风险小这个优化目标和收益大这个优化目标其实是冲突的
• 适用场景：基于问题所构建的优化目标函数不唯一，常出现在金融投资领域， 往往要求风险更小，收益更大

3) 线性规划

• 线性规划问题是要最小化或最大化一个受限于一组有限的线性 约束的线性函数
• 适用场景：所建立的目标函数和约束条件均为线性函数

4) 非线性规划

• 如果目标函数或者约束条件中至少有一个是非线性函数时，最优化问题叫做非线性规划问题
• 适用场景：所建立的目标函数或约束条件存在非线性函数

5) 整数规划

• 整数规划是指规划中的变量（全部或部分）限制为整数
• 适用场景：决策变量的取值只能为整数的情形

6) 二次规划

• 二次规划问题是目标函数是二次的，而约束条件是线性的
• 适用场景：所建立的目标函数或约束条件均为二次函数

7) 动态规划

• 基本思想是将待求解问题分解成若干个子问题，先求解子问题，然后从这 些子问题的解得到原问题的解
  • 背包问题：对于背包的类型，这边就做个简单的描述：n个物品要放 到一个背包里，背包有个总容量m，每个物品都有一个体积w[i]和价值v[i]， 问如何装这些物品,使得背包里放的物品价值最大。
  • 运输问题：给定m个资源，分配给n个部门，第i个部门获得j个资源a有个盈利值，问如何分配这m个资源能使获得的盈利最大，求最大盈利
  • 分割问题：给定一个具有$n$（$n<50$）个顶点（从$1$到$n$编号）的凸多边 形，每个顶点的权均已知。问如何把这个凸多边形划分成$n-2$个互不相交的三角形，使得这些三角形顶点的权的乘积之和最小？

8) 图论模型

• 最短路模型：主要包括Dijkstra算法和Floyd算法两种，用于求解两点间的最短距离
  • 适用场景：路径规划问题，如修建道路、设定救援路线等
• 最大流模型：通常可以把这些边想象成道路，流量就是这条道 路的车流量，容量就是道路可承受的最大的车流量
  • 适用场景：企业生产运输问题、交通拥堵优化问题等
• 最小生成树：图的生成树是它的一颗含有其所有顶点的无环连通子图,一 幅加权图的最小生成树(MST)是它的一颗权值(树中的所有边的权值之和) 最小的生成树
  • 适用场景：道路规划、通讯网络规划、管道铺设、电线布设等
• 排队论模型：排队论也称随机服务系统理论。它涉及的是建立一些数学模 型，以对随机发生的需求提供服务的系统预测其行为；排队论主要是对服 务系统建立数学模型，研究诸如单位时间内服务系统能够服务的顾客的平 均数、顾客平均的排队时间、排队顾客的平均数等数量规律
  • 适用场景：商店购货、轮船进港、病人就诊、机器等待修理等等

C. 聚类模型及应用场景

1) K-means聚类

• 针对每个点，计算这个点距离所有中心点最近的那个中心点， 然后将这个点归为这个中心点代表的簇。一次迭代结束之后，针对每个簇类， 重新计算中心点，然后针对每个点，重新寻找距离自己最近的中心点。如此循环，直到前后两次迭代的簇类没有变化。

• 适用场景：与地理位置有关的分类情形，如地物类别划分、村落划区、语言分 布位置划分等

2) 层次（系统）聚类

• 层次聚类也称系统聚类法，是根据个体间距离将个体向上两两聚合，再将聚合的小群体两两聚合一直到聚为一个整体。计算所有个 体之间的距离，最相近距离的个体合体，不断合体。
• 适用场景：通常用于行政区域的划分或分级处理等，如根据城市经济指标划分城市发展等级、根据各类综合指标进行文明城市建设评选等

3) 模糊聚类

• 基于模糊关系的分类法
  • 其中包括谱系聚类算法(又称系统聚类法)、基于等价 关系的聚类算法、基于相似关系的聚类算法和图论聚类算法等等。它是研究比较早 的一种方法，它不能适用于大数据量的情况，所以在实际中的应用并不广泛
• 基于目标函数的模糊聚类算法
  • 该方法把聚类分析归结成一个带约束的非线性规划问题，通过优化求解获得数据集的最优模糊划分和聚类。该方法设计简单、解决问题的范围广，还可以转化为优化问题而借助经典数学的非线性规划理论求解， 并易于计算机实现。
• 基于神经网络的模糊聚类算法
  • 它是兴起比较晚的一种算法，主要是采用竞争学习算法来指导网络的聚类过程

4) 神经网络分类

• 常用的分类模型为BP神经网络模型，指通过多层神经元系统建立 输入与输出间的非线性映射关系
• 适用场景：适合样本数量较多时的分类问题，常被用于图像地物类别划分

D. 评价模型及应用场景

1) 模糊综合评价法

• 模糊综合评判是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价，即用模糊-数学 对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清 晰，系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决
• 适用场景：无具体的评价标准，通过统计问卷等形式进行的评价问题

2) 层次分析法

• 是指将与决策总是有关的元素分解成目标、准则、方案 等层次，在此基础之上进行定性和定量分析的决策方法
• 适用场景：比较适合于具有分层交错评价指标的目标系统，而且目标值 又难于定量描述的决策问题，但常用于计算指标的权重

层次分析法是一种计算权重的方法，而模糊综合评价法是一种对问题进行综 合性评价的方法。进行模糊综合评价时，可使用层次分析法（AHP）对各个 因素进行权重赋值

3) 数据包络(DEA)分析法

• 它是根据多项投入指标和多项产出指标，利用线性规 划的方法，对具有可比性的同类型单位进行相对有效性评价的一种数量分析方法
• 适用场景：该方法一般用于评价生产效率或者综合竞争力水平等

4) Topsis综合评价法

• TOPSIS法根据有限个评价对象与理想化目标的接近程度进 行排序的方法，是在现有的对象中进行相对优劣的评价。TOPSIS法是一种逼近 于理想解的排序法，该方法只要求各效用函数具有单调递增（或递减）性就行。 TOPSIS法是多目标决策分析中一种常用的有效方法，又称为优劣解距离法。
• 适用场景：尝试用于大体系的综合评价，要求有理想化指标数据，如环境质量评价、医疗质量综合评价、国家综合实力评价等

5) 神经网络评价

• 与前面介绍的分类较为类似，事先将各项输入样本数据与其对 应的输出评价结果建立非线性映射关系，然后对未知样本进行类别划分即可
• 适用场景：同样适用于大样本的综合评价，不要求指标具有理想化情形

E. 预测类模型及应用场景

1) 灰色预测模型

• 是通过少量的、不完全的信息，建立数学模型并做出预 测的一种预测方法。是处理小样本（4个就可以）预测问题的有效工具， 而对于小样本预测问题回归和神经网络的效果都不太理想
• 适用条件：适用于小样本情况下的发展预测问题

2) 微分方程预测

• 无法直接找到原始数据之间的关系，但可以找到原始数据 变化速度之间的关系，通过公式推导转化为原始数据之间的关系。微分方 程建模是数学建模的重要方法，因为许多实际问题的数学描述将导致求解 微分方程的定解问题。把形形色色的实际问题化成微分方程的定解问题
• 常用到的模型有：传染病模型、理想火箭模型、人口模型（Malthus模型 和Logistic模型）

3) 回归分析预测

• 是在分析自变量和因变量之间相关关系的基础上，建立 变量之间的回归方程，并将回归方程作为预测模型
• 适用场景：样本数量较少，自变量与因变量间的变化具有明显的逻辑关系

4) 马尔科夫预测

• 对事件的全面预测，不仅要能够指出事件发生的各种可 能结果，而且还必须给出每一种结果出现的概率，说明被预测的事件在预 测期内出现每一种结果的可能性程度。这就是关于事件发生的概率预测。 马尔可夫（Markov)预测法，就是一种关于事件发生的概率预测方法。它 是根据事件的目前状况来预测其将来各个时刻（或时期)变动状况的一种 预测方法。马尔可夫预测法是地理预测研究中重要的预测方法之一
• 适用场景：主要用于市场占有率的预测和销售期望利润的预测以及其他商 业领域的预测等

5) 时间序列预测（必须掌握）

• 时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序 列的方法构 成数据分析的一个重要领域，即时间序列分析
• 时间序列预测法是一种定量分析方法，它是在时间序列变量分析的基础上，运用一定的数学 方法建立预测模型，使时间趋势向外延伸，从而预测未来市场的发展变化趋势，确定变量预 测值
• 常用到的模型：移动平均法、指数平滑法、差分指数平滑法、平稳时间序列模型 ：自回归 AR 、移动平均 MA 、ARMA 模型等
• 适用场景：常用在国民经济市场潜量预测、气象预报、水文预报、地震前兆预报、农作物病 虫灾害预报、环境污染控制、生态平衡、天文学和海洋学等方面。

5) 神经网络预测

• 大部分时间序列预测方法均假设各变量之间是一种线性关系，这种局限性 使其在实际应用过程中很难准确地进行分析和预测，而神经网络作为一种非线性模型被用来 研究预测问题效果会更好
• 常使用的方法：利用前i年的数据预测第i+1年的数据
• 适用场景：同样适用于大样本的预测问题

三、数学建模常用解题方法

数学建模常用解题方法分为三类：

• 关键词标定匹配法
• 案例等效替代法
• 逐步推理分析法

A. 关键词标定匹配法

将赛题对应的关键词勾画出来，然后根据其机理去匹配对应的算法

• 数据处理：补全、剔除、选取数据、分析数据、分析走势等……
• 关联与分析：原因、为什么？推测、两者关系、提出方案等……
• 分类与判别：分类、分级、判定、隶属、划分、异常值、识别等……
• 评价与决策：评价、评判、提出方案、选择方案、择优、后果等……
• 预测与预报：未来形势、走势、预测、变化、效果、未来、影响等……
• 优化与控制：调度、合理安排、选址、调整、优化、最优等……

B. 案例等效替代法简介

这类赛题主要针对工程性很强的赛题，案例等效替代法指的是 我们在进行赛题分析的时候，遇到含有关键字赛题无法找到能 够选用的模型，及模型应用条件无法嵌套，则可采用案例等效 替代法，及按照题干要求采取两种方法进行案例搜索，一种是 直接按照问题搜寻，另一种是排除问题主体的关键点搜索。通 过找寻类似的案例得到启发进行案例的延伸推广，将别人的解 题过程应用于自己的建模过程。

C. 逐步推理分析法

这类赛题主要针对数学物理较强的赛题，即给出的问题非常笼 统，含有较多的物理和数学知识，常用于美赛的A题，解决这类 题目一般无固定的常用模型可以套用，也没有类似的案例进行 比对，往往需要复杂的微分方程和物理学知识来解答。逐步推 理分析法的本质就是找到问题的关键点所在，对待求结果进行 一步步反推，将题目已知条件进行量化，利用复杂的数学或物 理学知识构建相应的关系式进行求解。