本文是李宏毅Machine Learning 2021 Spring 第三节课General Guidance的笔记，本节课主要讲解了深度学习的训练攻略

李宏毅ML2021-Spring-3: Neural Network Training Guidance

我们在前面的一节课以Youtube人数预测这个案例贯穿始终，在介绍Machine Learning / Deep Learning基础概念的同时，从线性模型入手，讲解了神经网络模型。

此外，我们还讲解了Machine Learning中训练一个模型的流程（Procedure）。我们复习一下，这三步分别是：

1. 定义模型（含参函数）
2. 定义损失函数（根据我们的数据）
3. 优化（训练）模型（神经网络是通过梯度下降）

然而其实神经网络中进行训练的时候，直接使用梯度下降往往会出现很多的问题，导致模型训练不出来。除此以外，我们上节课其实海遗留了不少问题，例如为什么神经网络要用Deep的而不是Fat的。这些内容在本节课都会进行讲解。

1. Framework of ML

我们首先规范化一下我们的（训练）模型（神经网络）时候整体的框架。

首先，我们根据我们需要完成的任务来收集数据，所有的数据被分为两部分，一部分是包含label的训练数据，而另外一部分是不包含label的测试数据：

• Training Data：${(x^1,\hat y^1),(x^2,\hat y^2),(x^3,\hat y^3),\cdots,(x^N,\hat y^N)}$
• Testing Data：${x^{N+1},x^{N+2},x^{N+3},\cdots,x^{N+M}}$

PS：其实，我们在手机数据的时候是不会划分测试数据和训练数据的，换而言之我们收集数据的时候都是$(x,\hat y)$这样的键值对。然后我们收集完数据之后再对数据进行拆分，其中一部分分为训练数据，而另外一部分分为测试数据。

这就意味我们其实是有测试数据的label的。但是注意，我们要当做没有，原因会在本文的后面讲解

而具体每一个具有label的数据，我们称为一个示例（example），即$(x^i,\hat y^i),i=1,\cdots,N$。在不同的问题中，$x^i$和$y^i$的表现形式不同。例如：

• 在语音辨识（Speech Recognition）问题中，$x^i$是输入的音频，而输出的$\hat y$是音素(Phoneme，类似于音标)
• 在图像识别（Image Recognition）问题中，$x^i$是输入的图片，而输出的$\hat y$是图片中的物品的名称/类别(Class)
• 在语者辨识（Speaker Recognition）问题中，$x^i$是输入的音频，而输出的$\hat y$是说话的人的名字
• 在机器翻译（Machine Translation）问题中，$x^i$是带翻译的文本，而输出的$\hat y$是目标语言的文本

接下来，有了训练数据和测试数据之后，我们就能够训练、测试我们的模型

• 首先是训练阶段

  1. 训练阶段的第一件事，就是定义出来一个含有位置参数的函数$y=f_\theta(x)$，注意，以后我们用$\theta$表示模型中的参数
  2. 接下来，我们要定义一个loss，loss是一个函数，因此有的时候又被称为loss function。Loss function的输入是模型中的参数，用于判定这组参数是好还是不好
  3. 最后一步就是求解一个Optimization的问题，即找一个$\theta^*$，能够让$L(\theta)$最小

  

• 在训练阶段之后，就是测试阶段

  1. 我们用得到的$\theta^*$来对所有的测试数据中的数据进行预测，即

     $$y^i=f_{\theta^*}(x^i), \qquad\qquad i=N+1,N+2,\cdots,N+M$$

  2. 接下来就可以用我们预测得到的${y^{N+1},y^{N+2},\cdots,y^{N+M}}$，例如把预测得到的结果上传到Kaggle上去（后面的课程的作业的要求）

2. General Guide

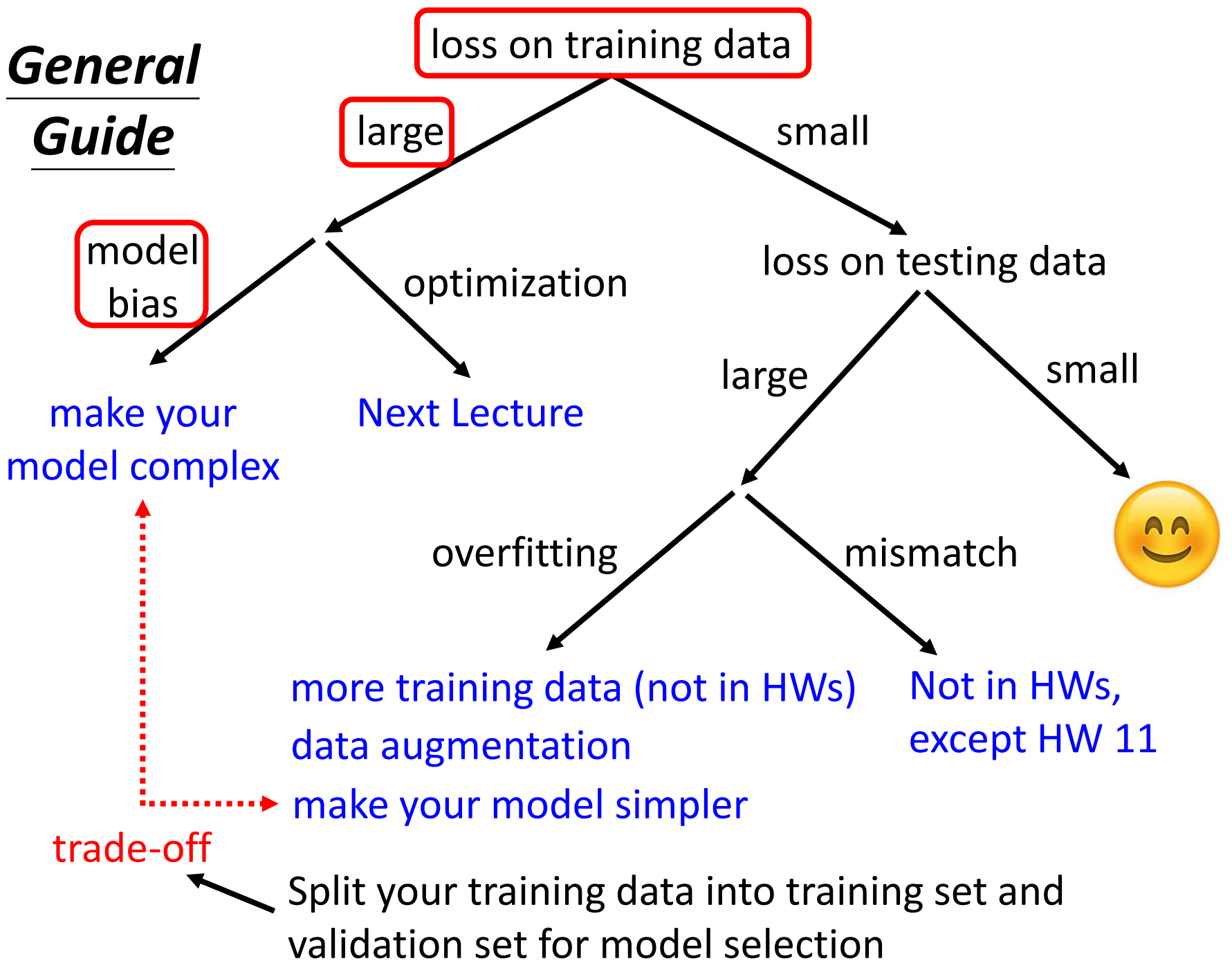
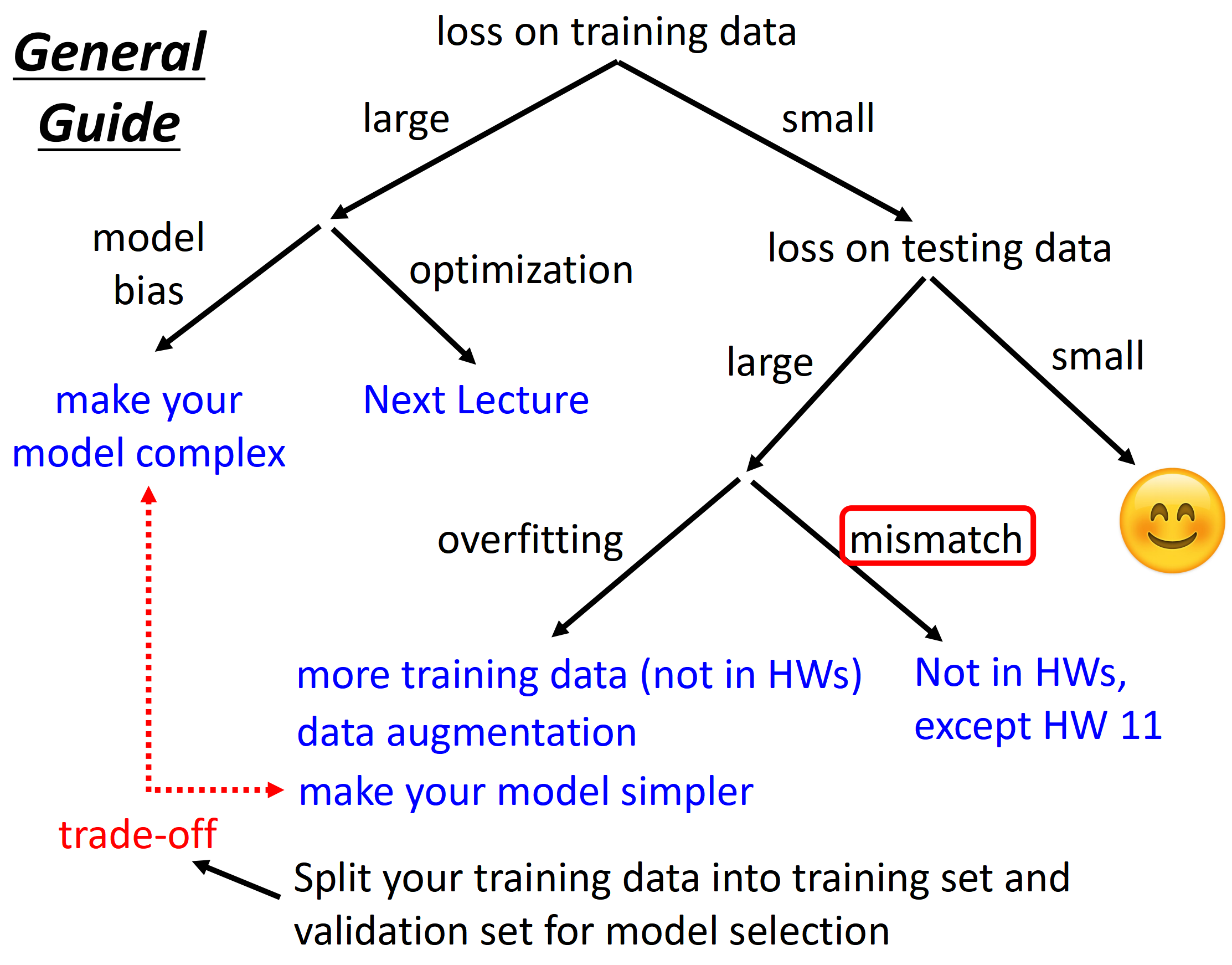
下面的这张图就是神经网络训练的攻略手册，可以帮助我们训练出来高精度的模型。当然适用于我们前期训练模型

整个攻略是从上到下的，因此当我们发现模型得到的精度不高，或者是模型根本没有训练起来的时候，第一步就是先检查模型在训练数据上的损失。

有人可能会问，为什么模型在测试集上的表现不好反而要先去检查训练集上的损失呢？

其实检查训练集上的损失是为了先检查模型有没有学习到东西。虽然说模型可能表现很差，但是通过这一步能看到模型训练时候的loss有没有下降，如果没有下降，那么就意味着很可能代码写错了

A. Large Loss on Training Data

我们如果检查发现，在训练集上模型的表现确实有提升，但是最终模型收敛到的loss却很大，那么此时就有两个可能，第一个是Model Bias，第二个就是Optimization的问题

1. Model Bias

对于Model Bias而言，其实在上周就已经讲过了。具体而言就是我们的模型太简单，其学习能力太弱难以充分的学习当前的任务。或者说模型的潜力太小，最终开发/学习到极致的模型也无法胜任当前的任务。

那么到底什么是模型的学习能力/潜力呢？

举例来说，我们现在设计了一个含有参数$\theta$的模型$f_\theta(x)$，即

$$y=f_\theta(x)$$

由于模型中的参数是可以变化的，而一个参数就对应一个具体的模型，例如$y=2x^2$和$y=3x^3$，这两个模型都平方模型这一类模型，但是却是两个不同的模型。

因此，我们让模型$f\theta(x)$中的参数$\theta$取不同的值，就有了不同的具体的模型，例如：$f\theta^1(x)$、$f\theta^2(x)$、$f\theta^3(x)$、$\cdots$、$f_\theta^N(x)$、$\cdots$

那么我们把这些模型当做高维（维数大于等于$len(\theta)$，因为可能存在参数更多的模型）空间中的一个点，那么我们把所有的模型集合起来，就可以得到一个模型的Set。

然而当前模型所构成Function Set太小了，无法包含到让模型损失最小的模型。换而言之，可以让Model表现最好的模型（模型由参数描述）是无法用当前模型来描述的

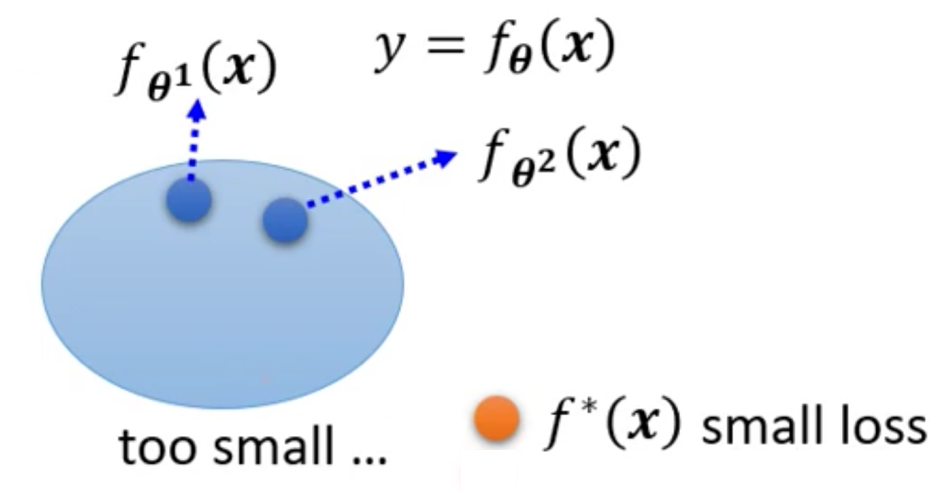
那么这个时候，即便是当前模型所能够描述的Function Set中最好的模型，他的Loss依然很高。

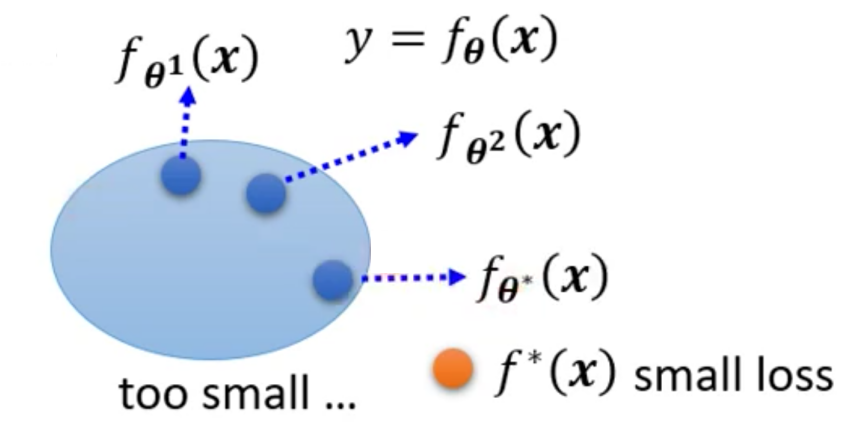
这个时候问题就类似于我们是在大海里捞针（表现最好的参数），然而大海里并没有针（当前模型并不存在全局/全模型最佳的参数）

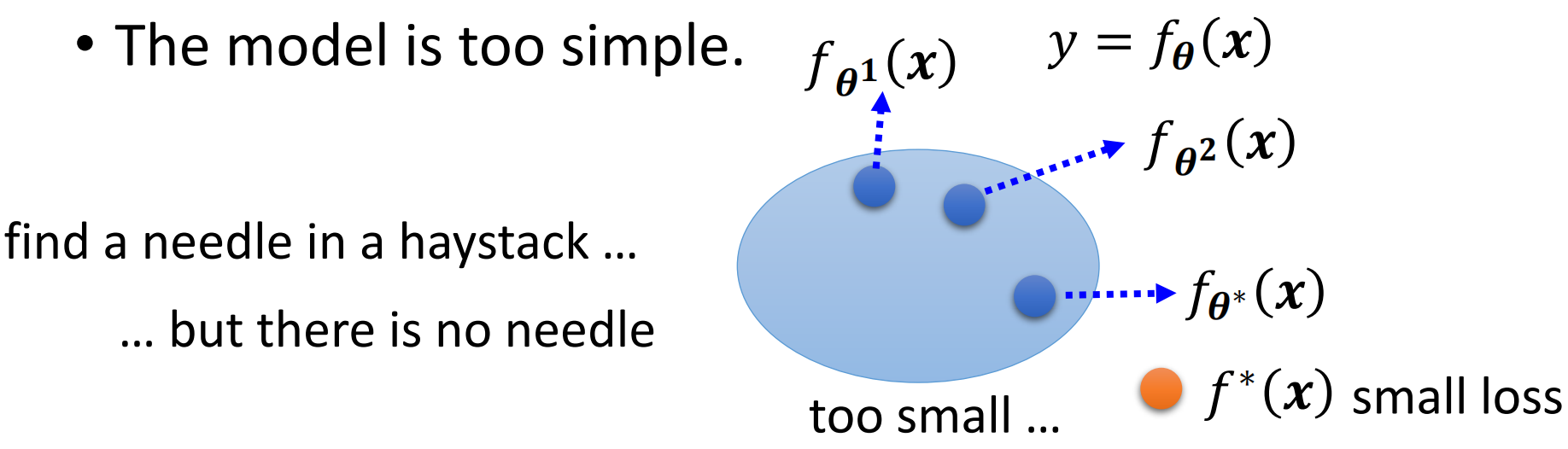
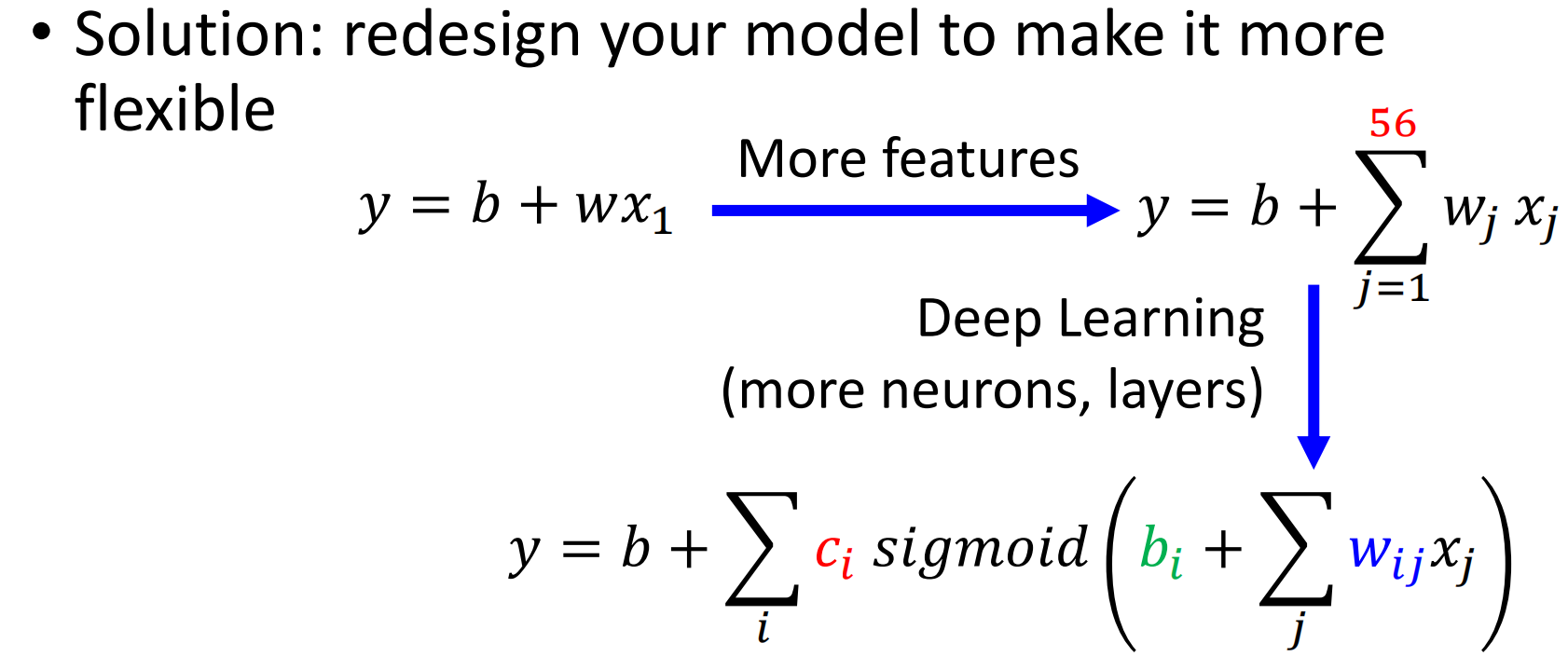
那么这个时候，我们要做的就是重新设计我们的模型，让他具有更大的潜力/更加可塑（more flexible）。所谓更加可塑，其实指的就是结构更加复杂、参数更加多、能够表达更多的模型。

这样的事情其实我们在上一节课就已经做过了，我们发现线性模型只看一天前的数据不太行，那么就让他看前56天的数据，然后觉得模型还是不太行，那么就引入Sigmoid、ReLu等函数为模型添加非线性、构成深度网络、神经网络

2. Optimization

在训练数据上loss大可能是由于Model Bias造成的，但并不是说所有的在训练数据上loss大就是由于Model Bias造成的，还有一种可能就是Optimization的问题。

所谓Optimization的问题，其实指的就是我们没有做好Optimization这一步。在我们的预期里，我们通过Optimization就能够让模型的表现得到提升，然而这都是建立在我们做好了Optimization这一步的基础山的，因此如果我们没有做好Optimization，模型的表现也是上不去的。

Optimization这一步出问题，其实由很多种可能，例如我们的学习率设的太大或者太小等等。当然，我们在上一节课其实也讲了一种Optimization中可能出现的问题，就是Local Minima的问题

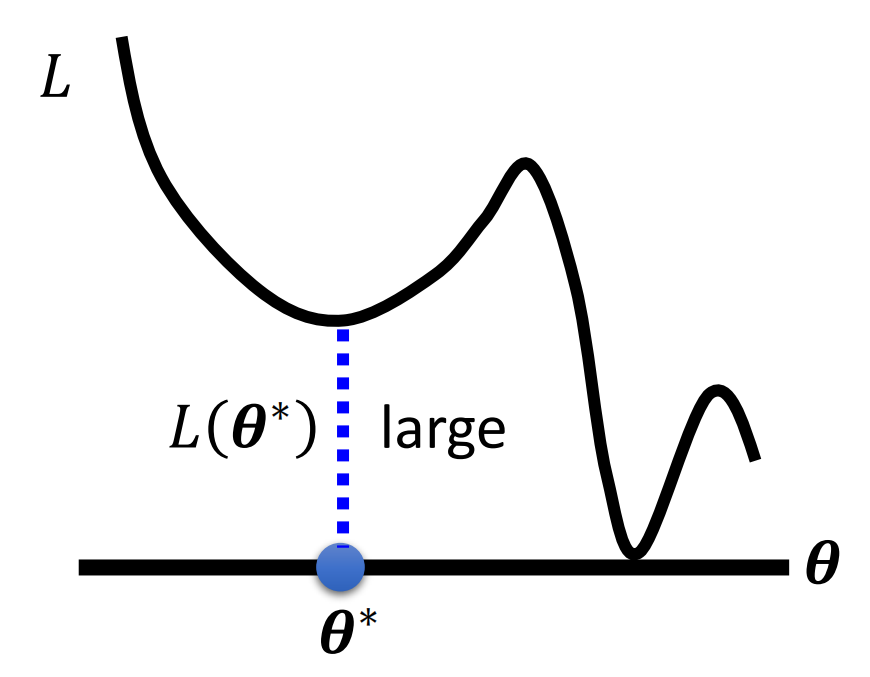
同样，用图像来形象的表示的话，就是问题的最佳的模型的参数确实可能由我们的模型来描述，然而在Gradient Descent的时候，由于某些原因（例如局部最优点），我们无法得到这个全局最优点。

形象的比喻，我们这个时候面临的问题就是针确实在海里，只是我们没有办法找到这根针

而对于Optimization做的不好的话，到底该怎么解决呢？

Optimization问题的Solution我们下节课再说。

3. Diagnosis between Model Bias and Optimization

那么这个时候问题来了，既然模型在训练数据上的表现糟糕可能是由Model Bias造成的，也有可能是由Optimization造成的。那么在当我们真实遇到了模型在训练数据集上的表现糟糕的情况的时候，到底那个才是我们的处境？

那么这个时候，判断我们所处的情况的关键就是我们的模型到底有没有足够的潜力，或者说我们的模型到底够不够flexible（可塑）？

那么这个时候我们可以通过下面的几个方法来进行判断：

• 通过不同的模型之间的比较来获得insight，即我们的模型是否足够的flexible

  举一个通过比较或者insight的例子

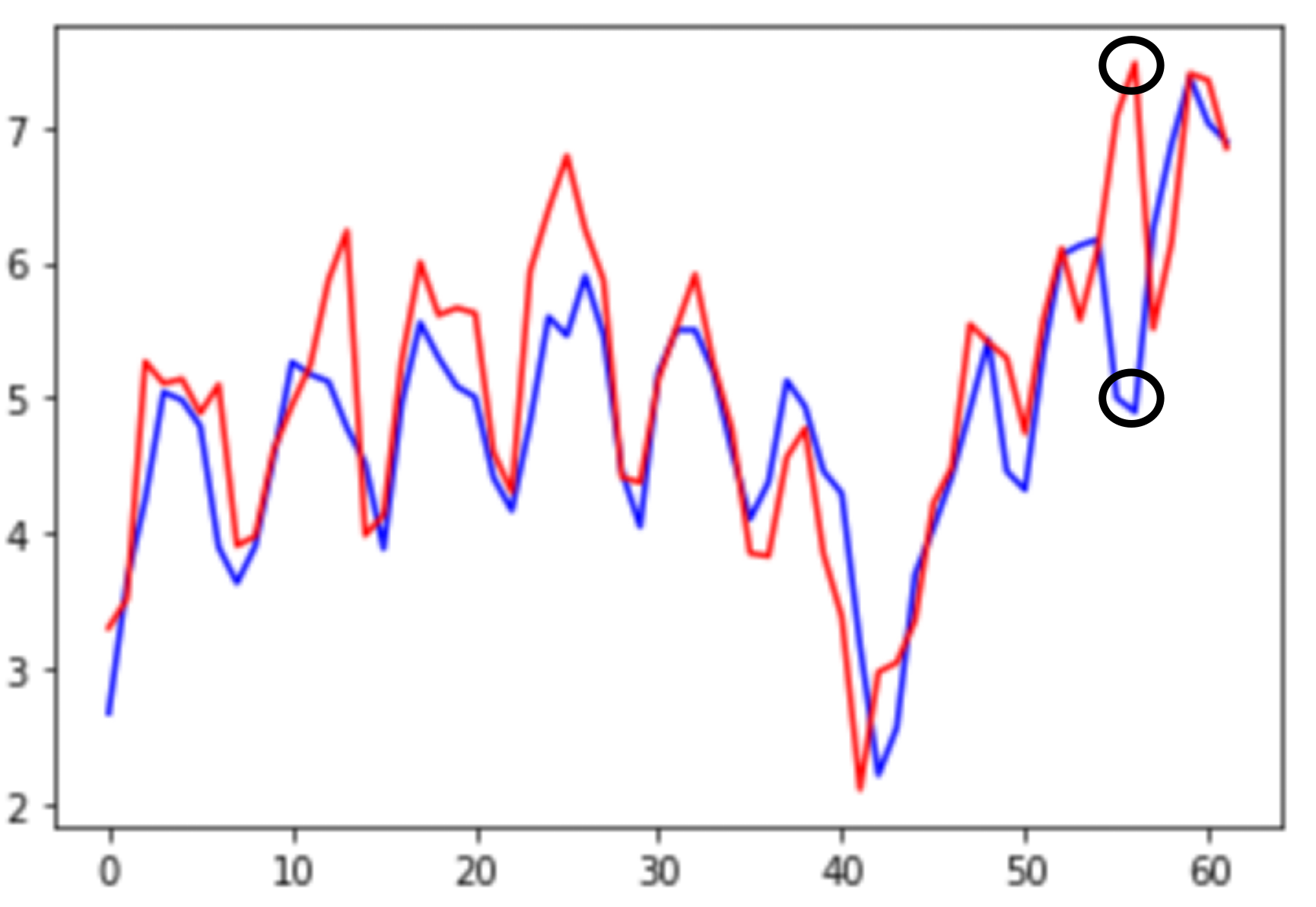
  这个例子是来自与2015年的Paper：Residual Network中的例子。这个Paper在一开头就讲了一个故事。这个故事是说，现在针对同一个任务，训练两个基本的结构相同而层数不同的Network。一个Network是20层网络，而另外一个是56层的模型。然后把这两个模型随着训练的进行，在测试集的表现记录了下来：

  

  在2015年的时候，大家对Deep Learning了解的还不是非常透彻。人们往往都认为，模型是越深越好的。一旦出现了上面的问题，就是Overfitting的问题（关于Overfitting后面会讲）。

  但是这个问题到底真的是由Overfitting造成的吗？这个不是由Overfitting造成的。虽然我们现在知道，Overfitting还要检查在训练集上的表现。

  可是在2015年ResNet的文章发现，如果发生了过拟合那么就应该是56层的模型的性能应该要优于20层的模型，因为56层毕竟都已经发生了过拟合（后面会介绍Overfitting，我们这里只需要知道Overfitting的一个特征就是在训练数据上表现超乎寻常的好而在测试数据上格外的烂）

  可以检查在训练数据上的表现发现即便是在训练数据上，深层的模型的表现也不好。因此，这个问题其实是20层的模型Optimization比56层的模型Optimization要容易。

  

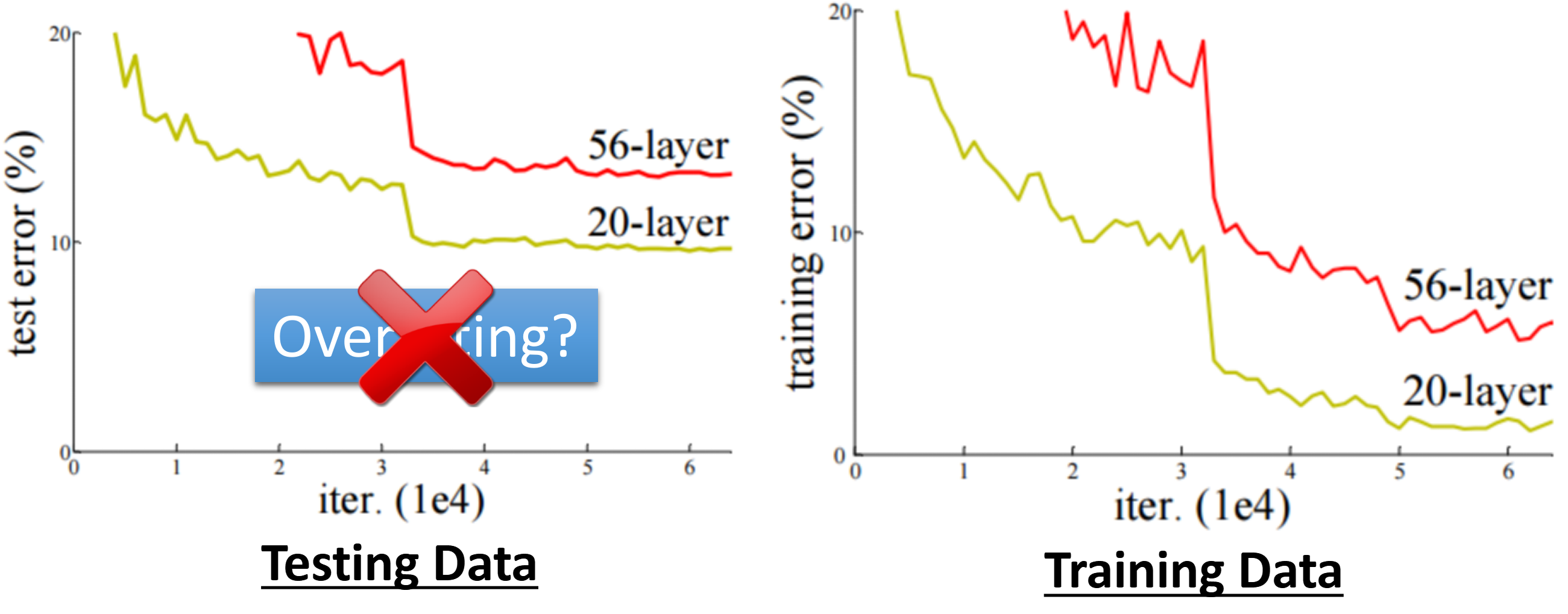
  因此当时认为这个是Overfitting的现象，其实是由于Optimization没有做好导致的。

  我们可能还有一个疑问，就是，诶，为什么说是Optimization没有做好而不是Model的Bias呢？

  其实我们在上面就已经说过了，一般来说，模型的参数越多，模型就越复杂，模型就更加的flexible。

  而且对于20层的模型来说，它能够做到的事情56层一定也能做到，就让前20层保持一样，后面的层全部复制前一层的输出就行了呀。因此56层的模型一定比20层的模型更加flexible。这就意味着，如果56层的模型Optimization成功的话，他的表现一定是比20层的模型要好的。

  因此，这个现象不是Overfitting，也不是Model Bias，而是Optimization做的不好

  

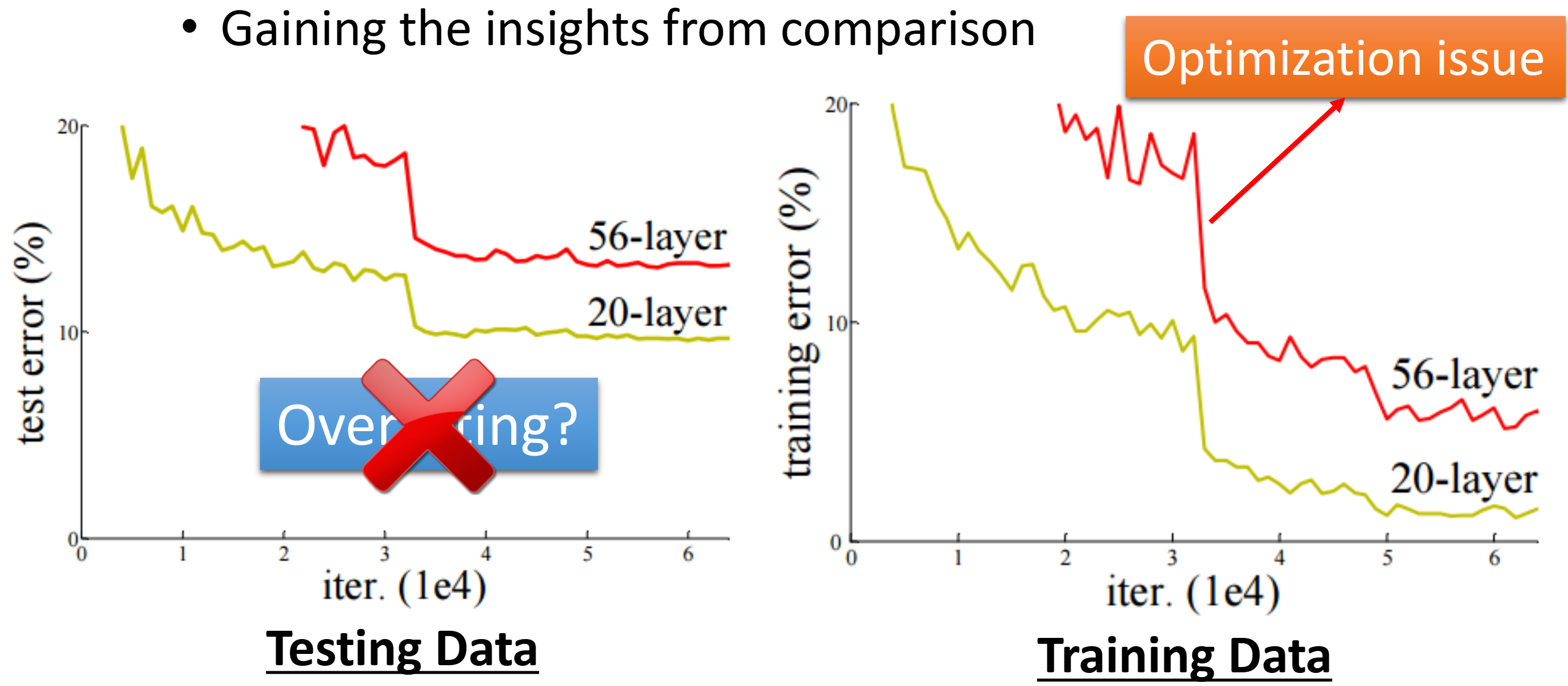
  所以上面这个例子给我们的启示就是（上面这个例子教会我们这样去判断是否是Optimization的问题）：

  1. 我们首先训练一个浅层的网络，因为浅层的网络不容易Optimization失败，或者我们可以用一些其他易于训练的机器学习的模型而不是神经网络，例如决策树或者支持向量机（Support Vector Machine）。

     用这些比较简单的模型训练得到的结果可以作为我们的下界

  2. 接下来训练一个比较深的Model、更加Flexible的Model。如果更加Flexible的Model的表现没有第一步简单的Model的表现好，那么就很有可能是发生了Optimization的问题。那么这个时候我们就需要通过一些手段来进行更加有效的Optimization。例如使用带有策略的Gradient Descent或者直接换一种优化的算法。

     举例来说，之前讲的YouTube观看人数预测问题。明明四层都能做到的事情五层却做不到，那肯定就是Optimization的问题了

     

B. Small on Training Data, Large on Training Data

那么接下来，假设我们通过努力，已经成功的让模型在训练数据上的表现变小了，那么我们接下来需要关注的就是模型在测试数据上的表现

1. Happy Ending

如果模型在测试数据上的表现也很小，那么其实就表明我们的模型已经很OK了，可以直接用于下一步了，所以这样就是Happy Ending

2. Small on Training Data, Large on Testing

A. Overfitting

在遇到了训练数据上loss小而测试数据上loss大，那确实有可能是遇到了Overfitting的问题。

但是要注意，Overfitting是在训练数据上的loss小而在测试数据上的loss大才可能会发生的，因此在判断发生了Overfitting这个现象之前，要先排除掉Model Bias和Optimization这两个问题。

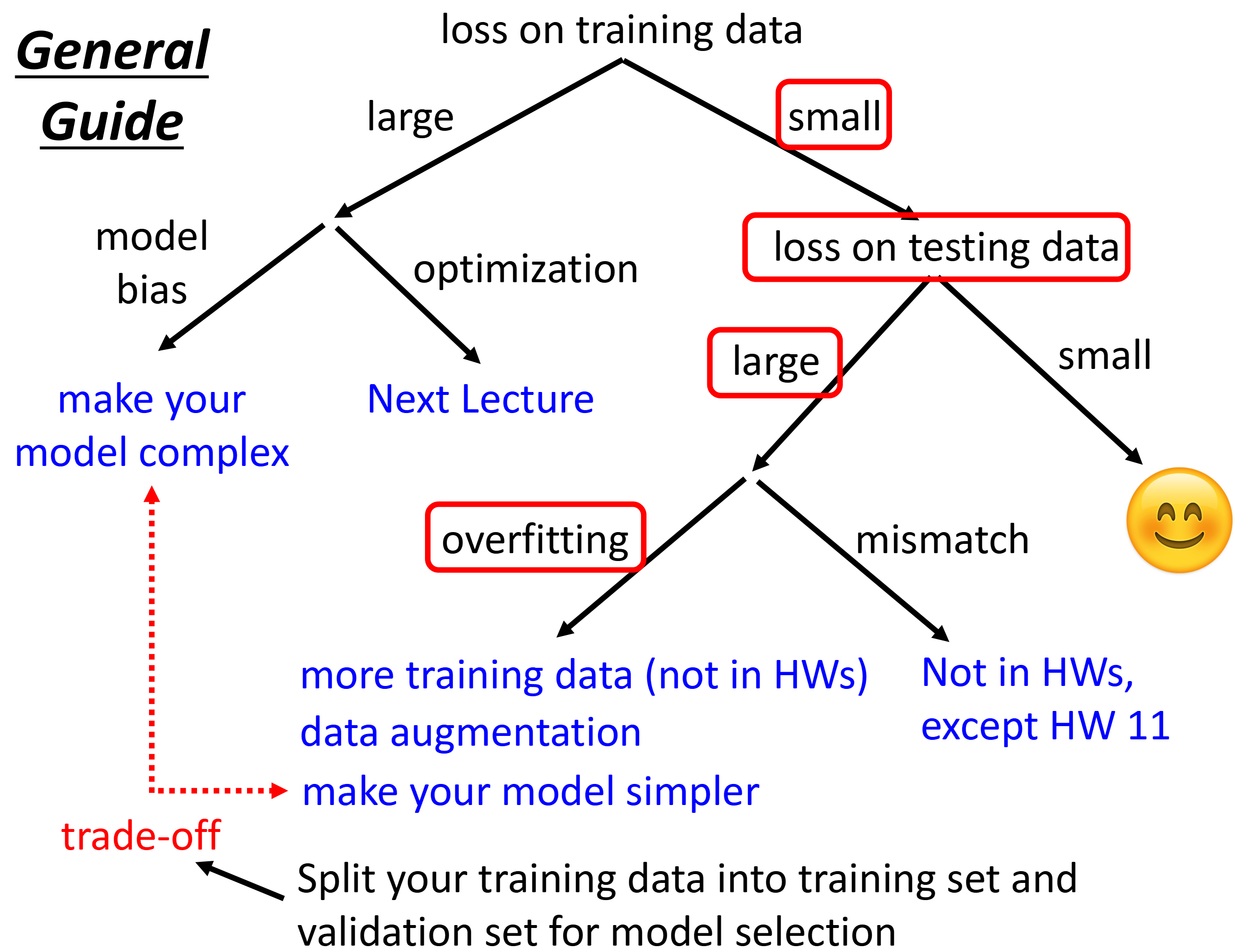
那么为什么会发生Overfitting（在训练集上表现好而在测试集上表现差的）问题呢？

我们下面通过举一个极端的例子来进行说明。

极端的例子

假设我们现在的训练集是${(x^1,{\hat y}^1),(x^2,{\hat y}^2),(x^3,{\hat y}^3),\cdots,(x^N,{\hat y}^N)}$

而我们通过训练之后找到了一个很废的模型，这个模型做的就是单纯记住见过的example。然后当见过的输入进来了知乎就能够给出正确的label作为预测，而没见过的输入进来了之后直接随便给答案，即

$$y=f(x)=\begin{cases} \hat y^i, &\exist x^i = x\\ random, & otherwise \end{cases}$$

那么这个模型其实一点用处都没有，因为完全不能用于帮助我们进行预测。可是即便是在测试数据上的loss很大，可是这个模型在测试数据上的loss却是0

当然，上面例子是非常极端的，一般是不会存在这样的模型的。我们下面举一个更加常见的例子

常见的例子

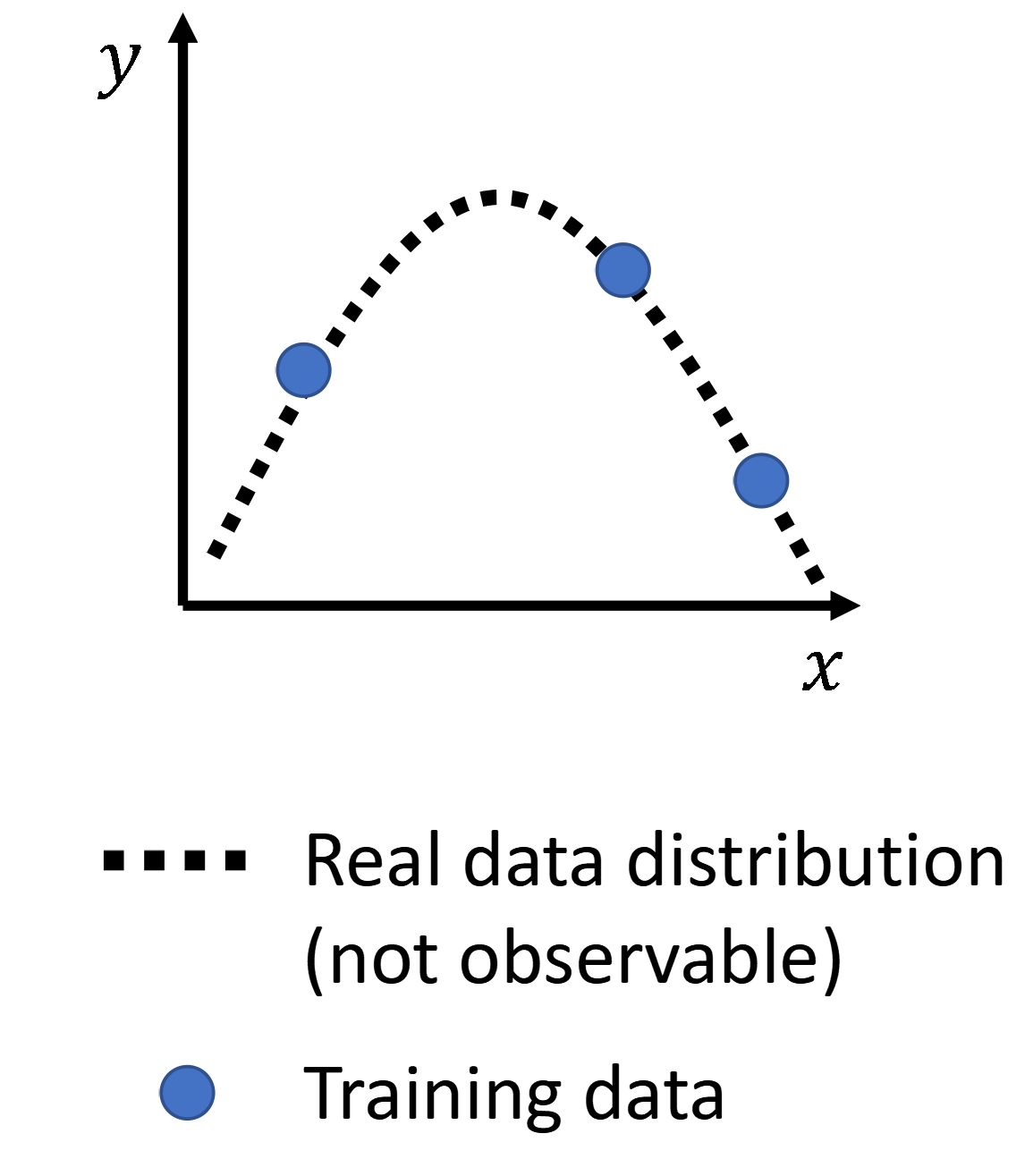
假设我们现在所有的example都是从一个二次曲线上获得的，那么我们现在的任务就是根据这有限个已知的点来预测未来给一个$x$，对应的$y$会在哪里。

那么对于我们来说，我们其实是通过有限次观测从曲线上采集得到的点，因此这个曲线的全体对于我们来说是不可见的。我们可见的只有这有限个数据点。

那么如果我们的模型非常的Flexible，那么就可以逼近更加复杂的函数。而为了让loss最小，我们Flexible的模型其实是有可能学成下面这样的模型。在我们有观察到的地方，模型还是好好的进行了拟合，而在没有采集到的地方，模型就有FreeStyle了

而我们的测试数据也是从真实数据的分布上观测得到的，而且往往和我们的训练数据不同，那么可想而知，学出FreeStyle的模型的表现肯定不好

那么该如何解决Overfitting的问题呢？

其实有两个解决的思路：

1. 第一个方向就是受到上面的例子的启发，Overfitting的发生是由于我们对原始数据分布的观测存在没有观测到的区域造成的。那么很简单，我们直接对其进行观测即可。换而言之，我们收集更多的数据来限制模型发挥它的Freestyle。那么这样模型能够发挥Freestyle的地方比较少，最后还是会很接近我们数据的原始分布

   

   为了要收集更多的数据，我们确实可以真的去收集数据然后来进行训练。可是这样的问题就是费时费力。

   一个替代的方案就是，我们根据我们对问题、对数据的认识来创造出来一些新的数据。例如对于图像识别问题来说，我们把图像水平翻转过来，或者把猫放大，那他都是猫。这一招叫做数据增强（Data Augmentation）

   

   但是我们在做Data Augmentation的时候要注意，不能随便乱进行数据增强，我们数据增强一定要有道理的。例如我们把一只猫翻过来。那么机器并不知道这只猫反过来了，反而认为猫有可能是浮在空中（毕竟机器没有学习背景、周围的环境，因此他没法发现周围的环境也反过来了），那么机器在学习的时候就会感到困惑，因为之前他学习的内容并没有说明猫可以浮在空中。因此用这样的数据来进行训练其实会降低模型的准确率，因为让他学到了错误的知识

   

2. 第二个方向就是从源头探究一下为什么会发生Overfitting。Overfitting发生的原因其实是模型的太大，模型能够学习到非常复杂的函数。而在损失函数的强迫下，模型不得不学习到更加复杂的、能够拟合所有训练数据的函数。因此，另外一种方式就是通过给模型增加限制，，限制模型的潜力，避免模型学习到复杂的函数。

   例如，对于上面的例子，我们somehow，通过某种方式（例如通灵），得知了模型是一个二次的曲线，即$y=a+bx+cx^2$。那么这个时候，模型能够学到的函数其实来来回回也就那么多种，因此我们的模型很有可能就会学到正确的函数

   

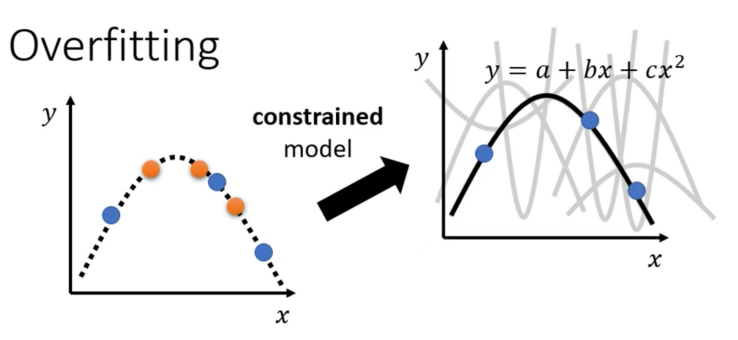
   而我们具体是怎么样知道这个模型就是一个二次函数的呢？其实这就依靠于我们的Domain Knowledge，或者说是先验知识。

   具体来说，有哪些方法来给模型添加限制呢？具体有下面的几种：

   1. 更少的参数（共享参数），对于神经网络来说就是更少的神经元
   2. 更少的feature
   3. Early Stopping
   4. Regularization
   5. Dropout

   关于3、4、5我们下节课再讲。不过关于更少的参数我们其实可以先简单的介绍一个例子

   

   对模型进行限制从而提升了模型表现的例子

   我们之前讲的网络的架构其实称为Fully-Connected Neural Network，即全连接神经网络

   

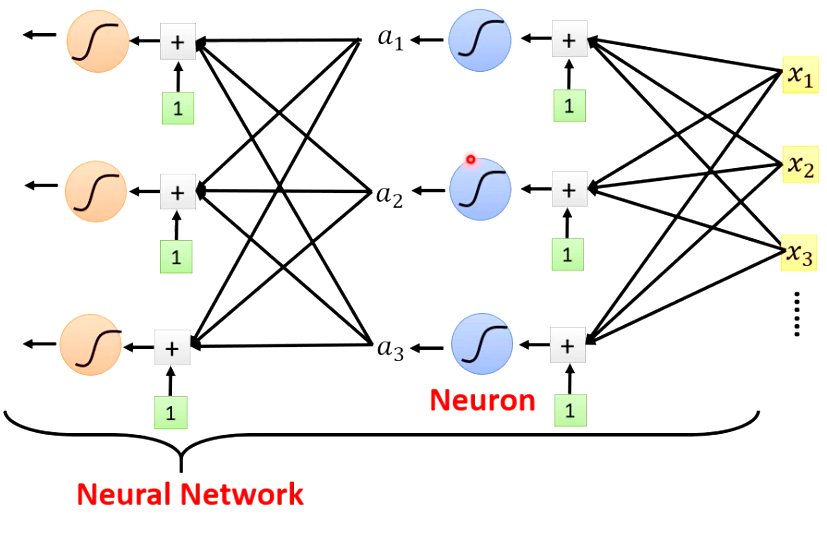
   而全连接网络其实是一个比较Flexible的model，这就意味这全连接网络的学习能力很强。与此同时带来的问题就是对全连接进行Optimization比较困难。或者说通过Optimization让全连接网络在任务上表现出色是一件比较难的事情，例如让全连接去进行图像识别就很难训练的好。

   而另外一种架构的网络称为卷积神经网络（Convolutional Neural Network，CNN），这种网络非常善于图像识别。但在实际上，卷积神经网络是一种限制非常大的网络，我们后面会具体讲到，对全连接网络添加参数共享，就成为了卷积神经网络。然而卷积神经网络这种限制是针对图像的特性进行的限制。换而言之，为卷积神经网络添加的这种限制限制了全连接神经网络学习到其他任务（例如语音辨识、文本翻译等任务）对应的函数。

   因此，CNN这个架构的网络能够表达的模型的集合其实是比较小的，是包含在全连接网络所能表示的集合的，如下图。然而，正是我们对全连接进行了这样的限制，提升了模型（在特定任务上）的表现。

   

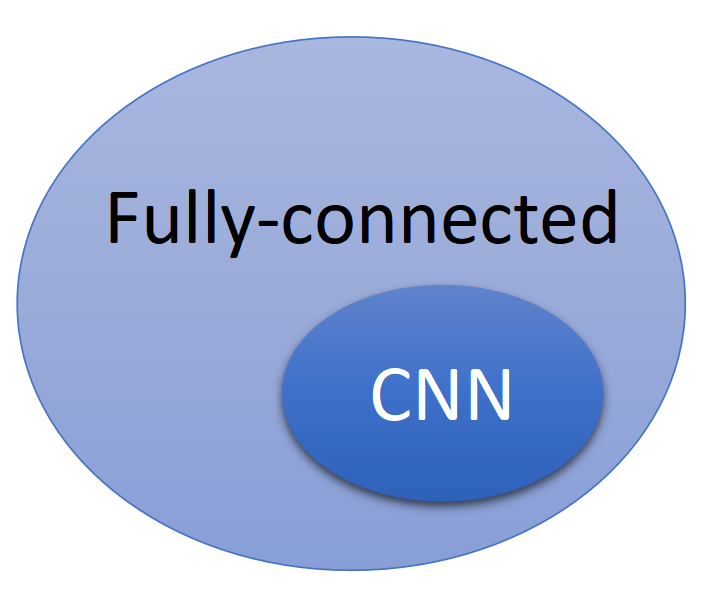
但是要注意，我们给模型的限制并不是越多越好，如果我们给模型的限制过多，就会导致模型的能力不足，从而出现Model Bias的问题。例如对于上面的问题，我们假设Model是一个Linear的Model，那么模型其实无法学习到一个非常满意的Model，因此最终极限的loss（最优的loss）还是会很大

那么其实到了这里，我们会发现有一个有点矛盾的地方，那就是我们让模型边的越来越复杂，越来越Flexible，那么模型Training时候的loss其实就会变低，但是模型在Testing时候的loss反而会变高，因此我们其实是需要在模型的能力和当前任务上的精度之间做一个取舍，选择一个中庸的模型

那么要怎么样去选择中庸的模型呢？这点我们在本文的后面：Cross Validation部分进行讲解

B. Mismatch

另外一种导致模型在训练时候的loss小而在测试的时候loss大的情况就是mismatch。

Mismatch指的就是训练和测试的数据是来自于不同的分布。例如我们训练的数据是从二次曲线上采集到的，而我们测试的数据是从三次曲线上来的。

在Mismatch的情况下，不管训练数据怎样的增加其实都没有用，因为要预测的数据的函数和学到的函数就是两码事。因此，Overfitting和Mismatch最大的区别就是对于Mismatch而言，单纯的增加训练数据没有办法提升模型的表现。

在这个时候我们就要注意我们的测试数据和训练数据的来源。

在绝大多数的情况下其实我们也并不会遇到Mismatch的情况。当然，现在也有不少的研究是关于如何处理Mismatch的情况。我们在未来的作业11就会专门的讲解处理Mismatch的方法。

作业11里面我们的训练图片是正常的图片，但是测试数据确实简笔画，那么模型其实不论怎么学其实都是学不好的。

当然除了作业11的情况，在作业一预测Covid19的确诊病例的时候我们如果用2020年的数据进行训练，而用2021年的数据作为预测，那么也会发生Mismatch的问题。原因也很好想，因为2020年的Covid19刚出来，人们还不是很有经验来应对Covid19，但是到了2021年，人们就有经验多了。

3. Cross Validation

A. Why not fine-tuning Model on Testing Set?

接上面Overfitting部分，我们说道要选出来一个中庸的模型

其实选择中庸的模型的根本目的还是选出来在Testing数据上表现最好的模型。那我们其实可能想到的一个方法，就是不断地做在Testing上跑模型、计算分数，然后选择出来在Testing上表现最好的模型。例如在Kaggle上（老师的作业有一部分是以Kaggle），计算分数是根据在Testing的数据上计算得到的。而所有的Testing的数据又被分为两部分，一部分是Private的Testing数据，另外一部分是Public的Testing数据。

对应到我们真实的场景中，我们收集的数据被分成了两部分，一部分是Training Set，另外一部分就是测试数据，对影Public的Testing Set。而在我们的模型部署上线后见到的真实的业务数据就是Private的Testing Set。

那么假设我们现在有三个模型，这三个模型我们并不知道用哪个好，然后我们就在Public的Testing上来进行挑选。将选好的模型用于Private的测试，得到最终的分数，那么最终的分数其实有可能会更低。

具体的原因，我们同样用一个非常极限的例子来阐述。模型同样只是记住数据，而对没有见过的数据随机给出结果。那么由于所有的模型都没有见过Testing的数据，而有可能编号56789的模型给出的Random的结果更好，然后我们用这个模型选为最终的模型，在Public Testing上测试。

而由于在Private的测试数据上计算最终分数是在ddl结束之后，因此很有可能发生的事情在Public上表现好的模型在Private上表现糟糕

那么这个原因又是为什么呢？

这个原因其实就是我们过拟合了测试数据。因为测试数据毕竟也是我们收集到的有限数据，因此我们不断地用测试数据来进行测试的话，那么其实就相当于我们在不选选择在我们收集到的Testing的数据上表现良好的模型。然而真实的数据是无穷的，我们只看模型在Testing数据上的表现，就和我们在训练阶段只看Training数据上的表现一样，发生了过拟合。

因此我们其实是不能够用Testing的数据来帮助我们选择模型的。

B. Fine-tuning on Validation Set

那么我们既然不能够用Testing Set来进行调试，那么我们该怎么样来挑选模型呢？这个方法就是进行Validation，即对模型进行验证。

具体而言，就是我们把训练数据再拆成两部分，随机取其中的10%作为Validation Set，剩余的90%作为Training Set。然后我们所有的模型用Validation Set来测试其好坏。我们根据在Validation Set上的表现，选出最好的模型，然后在Testing Set上进行验证。这样做的话，我们如果进行大量的调试的话，过拟合的其实是Validation Set。那么这个时候，使用Testing Set就可以真实的测试出来我们模型的好坏了。此时，对于我们采集的Testing Set还是我们模型部署上线后业务中真实的数据对于模型来说都是没有见过的数据，因此表现会非常稳定。

当然，由于我们还是有Public的Testing数据因此我们在见到在Public的Testing Set上的表现后还是忍不住的会去调试。这个时候就建议不要调试太多次，否则最终还是会过拟合Public Testing Set。最好的其实就是只看Validation Set的结果，而不去理会Public上的数据

C. N-fold Cross Validation

我们上面介绍了为什么要做Cross Validation以及怎么做Cross Validation。那么就存在一个问题，因为Validation Set的选取是依赖于我们的选法的。因此我们如果在选在Validation Set的时候存在偏差，那么就有可能导致我们Validation的结果是偏低或者偏高的。

换而言之，可能会由于我们的选法导致选出来了奇怪的Validation Set，进而导致无法真实的反映模型的性能，因此模型最后的性能可能很差。因此，为了处理这种问题，我们就可以用N-fold Cross Validation。

N-fold Cross Validation指的是把训练集切成N等份。然后取其中的一份作为Validation Set，剩下的作为Training Set，然后训练得到结果。然后更换Validation Set，继续训练然后得到结果，这个过程重复N次，得到N个结果。最后N个结果平均就得到了最终的结果。

4. 上周的结果

最后在上节课结束的时候，老师让同学们选择模型来预测这个周的视频的观看人数。最后大家选择了三层的模型。

那么最后的结果如下，可以看到，大家上周猛点老师的YouTube，让模型的表现烂掉😂