本文主要介绍了数学建模中的一类知识:相关性分析
数学建模算法9-相关性分析
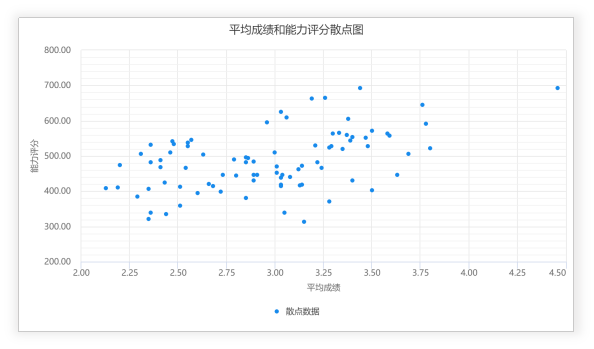
相关性,是指两个变量的关联程度。一般地,从散点图上可以观察到两个变量有以下三种关系之一:两变量正相关、负相关、不相关。
- 如果一个变量高的值对应于另一个变量高的值,相似地,低的值对应低的值,那么这两个变量正相关。在土壤中,孔隙率和渗透度就具有典型的正相关。
- 反之,如果一个变量高的值对应于另一个变量低的值,那么这两个变量负相关。
- 如果两个变量间没有关系,即一个变量的变化对另一变量没有明显影响,那么这两个变量不相关。

而相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度。
之所以要进行相关性分析,是因为在数学建模中经常会遇到一类题目,会评价两个指标(变量)之间的关系/联系。因此,本文就将介绍相关性分析的相关知识。
1. 变量间的相关性
在统计学上,我们通常这样判断变量之间是否有关:
- 如果一个变量的取值发生变化,另外一个变量的取值也相应发生变化,则这两个变量有关。
- 如果一个变量的变化不引起另一个变量的变化则二者无关。
在变量相关的基础上,我们又会有两个变量的相关程度到底如何,即一个变量变化多少另外一个变量对应的会变化多少?
因此我们定义变量关系强度,即两个变量相关程度的高低。统计学中是以准实验的思想来分析变量相关的。通常从以下的角度分析:
- 两变量是否相互独立
- 两变量是否有共变趋势
- 一变量的变化多大程度上能由另一变量的变化来解释
2. 四种基本变量
根据变量的类型,现实中的变量可以分为下面四种:
- 定类变量:根据定性的原则区分总体各个案类别的变量,变量间没有大小关系。例如:性别,民族、婚姻状况
- 定序变量:区别同一类别个案中等级次序的变量,变量间具有大小关系,但是没有数值关系。例如:文化程度、工厂规模、年龄大小
- 定距变量:区别同一类别个案中等级次序及其距离的变量,变量间具有大小关系且具有数值关系(可以用数值描述的变量),例如:摄氏温度、比率、智力水平。此外,定距变量是没有零点的,零只是其中的一个值。而且,加减得到的差值有意义而乘除后的值没有意义。
- 定比变量:也是区别同一类别个案中等级次序及其距离的变量,除了具有定距变量的特点外,还具有零点,即零点相比于其他值有意义,例如:收入、价格、市场占有率
3. 两变量的相关分析
A. Pearson相关系数
1. Pearson相关系数的计算
适用于定距、定比类型的变量。 是运用最广的一种相关程度统计量。例如可以用皮尔逊系数分析收入和商品价格的相关性。
皮尔逊系数$r$的计算如下:
Pearson系数的相关性检验用$t$检验,其统计量$t$服从自由度($n-2$)的分布,其中n表示数据的维度
之所以需要对皮尔逊系数进行检验,原因在于我们对一个变量的值的采集是通过有限次的观测。因此就会存在偶然性的问题,所以需要进行相关性检验
- 若计算得到$t\ge t_{a/2}$或$p\ge a$,则认为$r$统计显著。例如变量十六个维度($n-2=14$),且$a$取0.05,若计算得到$t\ge2.145$,则有95%的概率认为两个变量相关这一结果不是偶然造成的,或者说有95%的把握认为两个变量相关。
- 若计算得到$t\leq t_{a/2}$或$p\leq a$,则认为$r$统计不显著,即非常有可能是偶然因素造成的

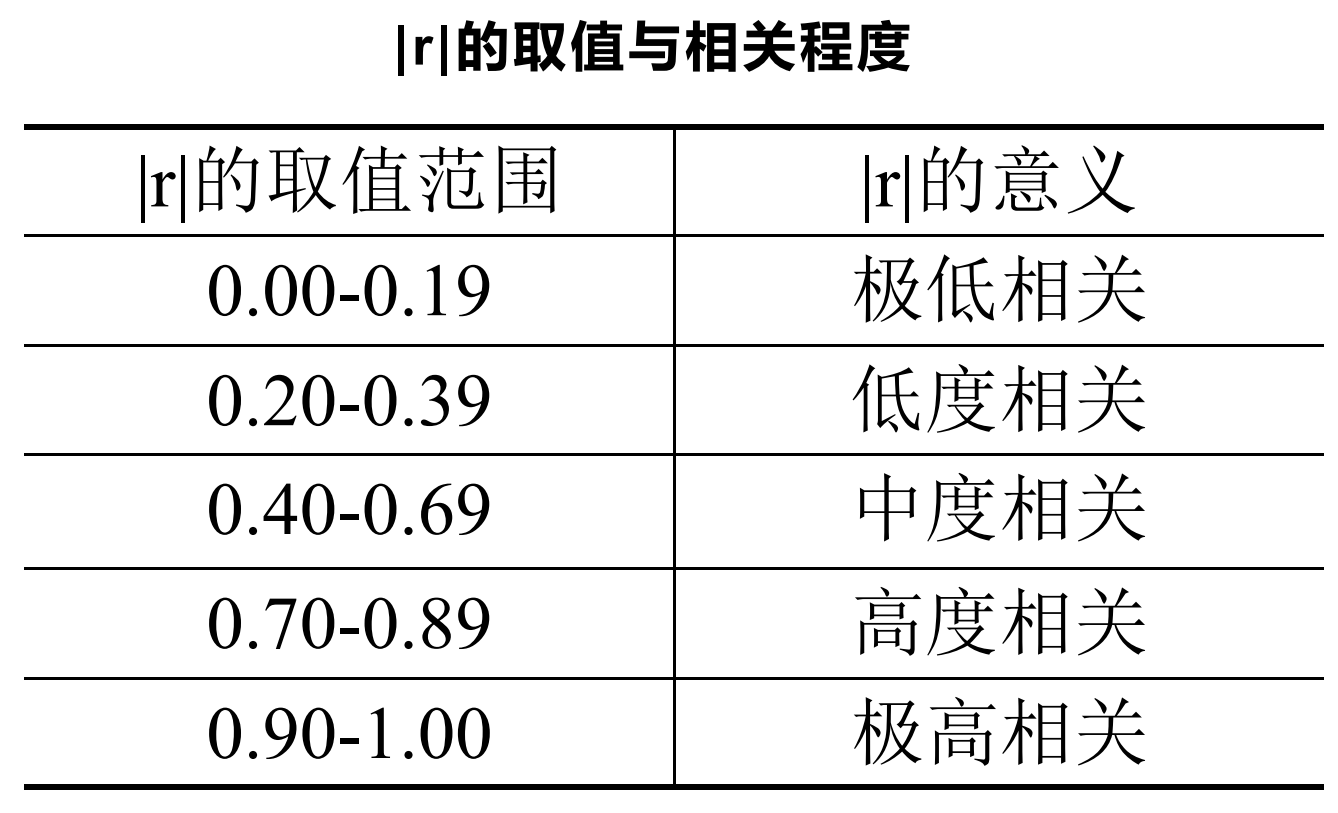
2. Pearson相关系数的意义
对于皮尔逊系数而言,其越接近一,表示计算该皮尔逊系数的两个变量之间相关性越高
3. Pearson相关系数的使用条件
- 两变量均应由测量得到的连续变量。
- 两变量所来自的总体都应是正态分布,或接近正态的单峰对称分布
- 变量必须是成对的数据
- 两变量间为线性关系,因此计算前需要先画散点图查看一下
B. Spearman相关系数
1. Spearman系数的计算
Spearman系数是用于计算度量定序变量与定序变量之间的相关系数。
斯皮尔曼系数计算如下
其中,$x_i$,$y_i$是两个变量按照大小排序的等级,$n$为样本容量。在$n\ge 20$之后,可以用$t$统计量进行检验。
同样,
- 若计算得到$t\ge t_{a/2}$或$p\ge a$,则认为$r$统计显著。例如变量十六个维度($n-2=14$),且$a$取0.05,若计算得到$t\ge2.145$,则有95%的概率认为两个变量相关这一结果不是偶然造成的,或者说有95%的把握认为两个变量相关。
- 若计算得到$t\leq t_{a/2}$或$p\leq a$,则认为$r$统计不显著,即非常有可能是偶然因素造成的
C. 双变量关系强度测量的主要指标
双变量关系强度测量的主要指标如下