本文是李宏毅Machine Learning 2021 Spring 第二节课Introduction of Machine / Deep Learning的笔记，本节课主要结合案例讲解了机器学习/深度学习的基本概念

李宏毅ML2021-Spring-2: Introduction of Machine/Deep Learning

1. What is Machine Learning

到底什么是机器学习呢？

从一个角度来说，机器学习其实就是让机器去找函数，例如：

• 对于语音识别来说，函数的输入是一段语音信号而输出是这段语音信号对应的文本
• 对于图像识别来说，输入是一张图片，而输出是一段描述图片类别的文本
• 对于下围棋来说，函数的输入是当前棋盘上的状态，输出是机器下一步落子的位置

从上面的例子我们能够想象得到这些函数会非常非常复杂，人类没有办法写出他们的解析式，因此我们预期希望机器能够自动寻找这个函数

2. Different types of Functions

因为要找的函数不同，机器学习可以分为不同的类别。下面就是一些专有的名词：

• Regression: 机器需要寻找的函数的输出是一个（连续的）数值

  例如，让机器预测未来的PM2.5的数值。函数的输出是明天中午的PM2.5的指数，而输入则是今天可能影响到明天PM2.5数值的因素的值，例如今天的PM2.5、今天的问题、今天的臭氧浓度等等。像这样，寻找输出是一个连续数值的函数的任务就是Regression的任务

  

• Classification: 机器的输出是多个选项中正确的一个（类别） ，这些选项都是人类提前给定的

  例如，让机器判断一封邮件是不是垃圾邮件。那么机器的输入就是这封电子邮件，而输出就是Yes或者No两个选项中的一个。

  

  当然，Classification任务的选线可以不止有两个，像上面这样只有两个选项的Classification任务是Binary的。而对于下围棋来说，我们如果把棋盘上$19\times19$个可以落子的位置当做$19\times19$个类的话，那么让机器下围棋这个任务就是一个有$19\times19$的选择题，让机器从$19\times19$个选项中选出正确的选项（下一步要下的位置）

  

然而Classification和Regression都只是机器学习任务中的一小部分，还有一类很大的问题，即Structure Learning

• Structured Learning: 机器不只需要做选择题、产生一个数字，还要去产生一个有结构的物体。例如让机器去画一张画、写一篇文章。形象的理解就是让机器学会创造

3. Case Study: How does machine find a function?

A. Background

自从2014年开始上课以来，李宏毅老师就会把自己的课程视频上传到YouTube频道上。

而对于一个YouTuber来说，他最在意的就是这个频道的流量有多少。因为对于一个全职Youtuber来说，流量决定了一个YouTuber的收益有多少。

那么我们就想，能否找到一个函数输入是YouTub后台的数据，而输出是未来的点阅率

B. How to find the function?

接下来我们就要问该怎么样寻找这个输入是今天的数据，输出是未来数据的函数呢？

那么对于机器学习来说，整个过程分为三步

1. 第一个步骤就是写出一个带有未知参数的函数解析式。简单来说就是我们先猜测一下这个函数$f$的到底长什么样子。

   那么我们先猜测一下，这个函数可能是下面这样

   $$y=b+wx_1$$

   其中$y$是明天的观看人数，例如2月26号的观看人数，而$x_1$是今天的观看人数，例如2月25号的观看人数；$b$和$w$都是未知的参数，后面我们准备让机器学习的就是这两个未知的参数

   那么我们为什么猜测这个函数会是$y=b+wx_1$这个样子呢？其实这个猜测是来自于我们先前对这个问题的理解，即我们的domain knowledge。而常听有人会说做机器学习需要一些domain knowledge，那其实domain knowledge的左右就是帮助我们写出来这个函数解析式。考虑到在真实的一个神经网络中，模型就是我们需要找的一个函数，因此domain knowledge的作用就是指导我们该如何设计网络。

   对于上面的问题来说，我们的domain knowledge就是明天的观看人数应该会和昨天的人数有关。虽然有关但又不是相同，因此我们就乘以一个数字在加上一个数字 。而我们猜测得到的带有未知参数的函数就称为我们的Model

   我们的猜测是基于我们现有的认识（现有的Domain Knowledge）提出的，而由于我们的认知是受限的，我们的模型又是在当下的认知下提出的，因此可能不对，或者说表现不佳。那么未来随着我们对问题研究的深入，我们对问题的认识越发深刻，我们就可以根绝我们更加完善、正确的Domain Knowledge来指导我们修改模型。

   例如明天的观看次数是不是有可能和过去几天都有关系？也即今天一天的观看人数无法完全决定明天的观看人数。当然这需要我们对问题进行探索，验证当前的Domain Knowledge才行。

   

2. 定义一个Loss。Loss其实也是一个函数，这个函数的输入是我们函数的参数，即

   $$L=L(b,w)$$

   而Loss这个函数输出的值就是值当前的参数的好坏，好坏的衡量可以用一个数值来描述（有点模糊数学隶属度的意思）。

   这样说比较抽象，我们举一个具体的例子。假设，我们现在让上模型中的参数$b=0.5k,w=1$，那么我们的模型就变成了

   $$b=0.5k,w=1 \rightarrow y=0.5k+x_1$$

   那么上面$y=0.5k+x_1$这个模型到底有多好呢？这就是Loss来衡量的。

   

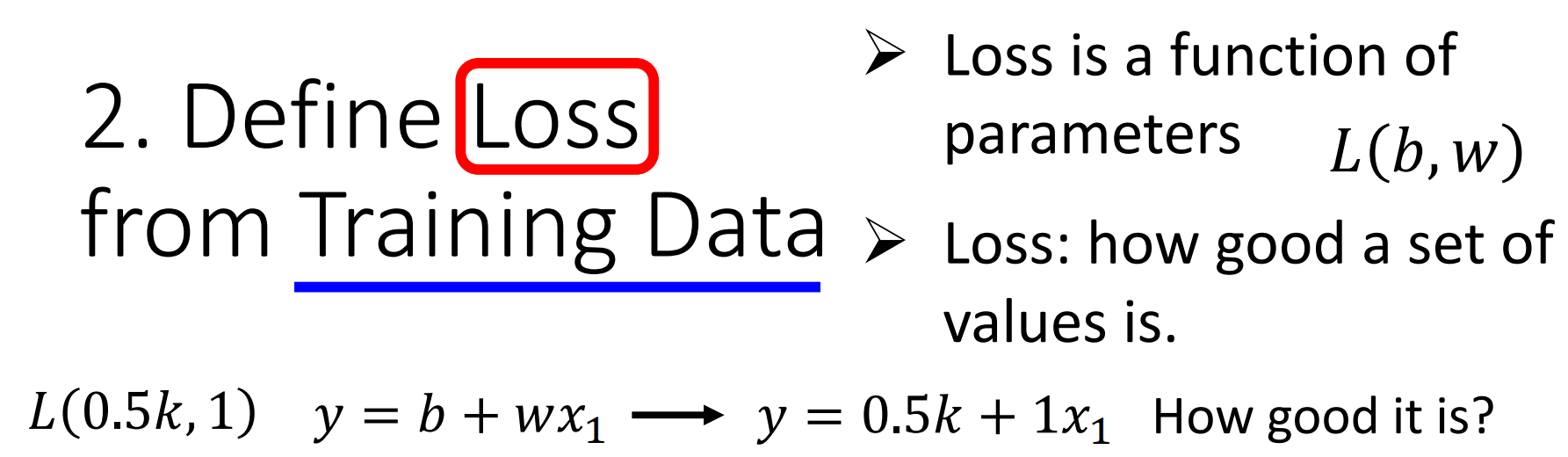
   而要衡量Loss就要从训练资料来入手。假设我们现在的输入的数据是从2017年1月1日到2020年12月31日的观看数据。那么我们就可以通过下面的方式来计算Loss。

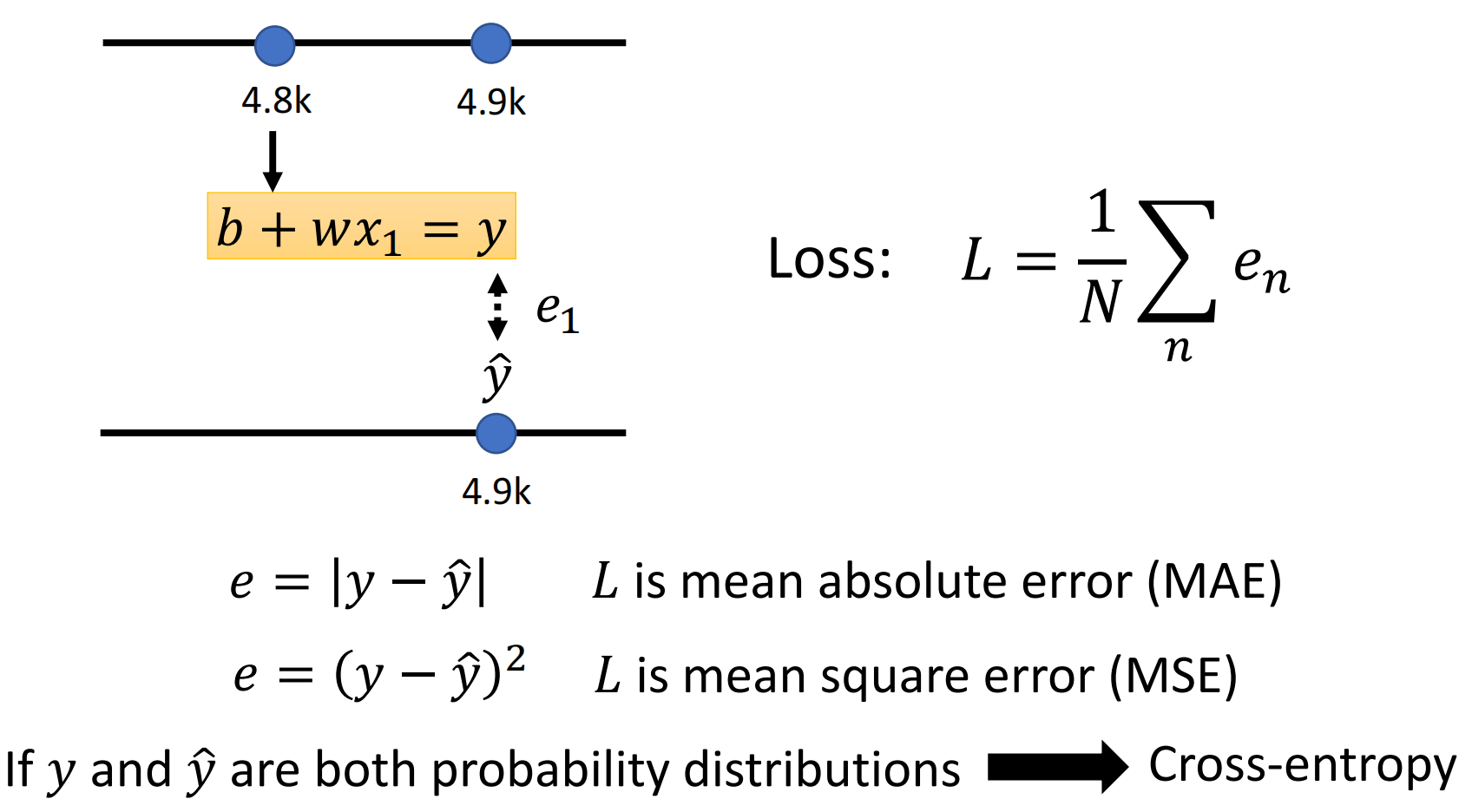
   我们把2017年1月1日的观看人数带入到模型中去，计算得到模型预测的2017年1月2日观看的人数为5.3k，接下来我们用模型预测的结果和真实的值来进行比较，计算得到一个误差$e_1$。这个真实的值就称为label。当然误差计算的方式不止一种，我们这里就去绝对值，即$e_1=|y-\hat y|=0.4k$

   当然，我们现在有的数据不止有1月1日这一天，我们也可以用1月2日的值预测1月3日的值，然后计算$e_2$。

   

   同样的方法，为我们可以算到三年来每一天预测的误差。然后我们把这三年的误差加起来取平均，就得到的了模型在所有数据上的表现。而这个平均的Loss越大，就表明模型的表现越差。

   此外，计算Loss的方法不止一种，我们上面是对绝对值取平均，因此称为Mean Absolute Error（MAE），此外还有Mean Square Error（MSE）的Loss

   我们这个任务很明显是一个Regression的任务，而对于Classification的任务，我们的loss function就可以取Cross-Ectropy Loss

   

   对于$y=b+wx_1$这个模型，我们可以取不同的$w$和$b$计算得到一个loss surface，下面就是这个模型用真实的数据计算得到的Error Surface。越偏红色系Loss就越大，而越偏蓝色系Loss就越小。绘制的线是等高线。

   

3. 机器学习的第三步就是Optimization问题，即找到让模型的Loss最小的参数。对于上面的问题，我们要找的就是让模型loss最小的$w$和$b$，将其记为$w^*$和$b^*$，那么优化这一步就是

   $$w^*,b^*=arg\min_{w,b} L$$

   在数学上求解优化问题有很多方法，我们这里只讲Gradient Descent这一种方法。为了简单起见，我们线假设$b$不动的情况下，寻找让Loss最小的$w$

   那么$w$取不同的值的时候，就会得到一条Loss曲线。那么我们的目的就是找到这个loss曲线中最低的那一个点。

   

   Gradient Descent的步骤如下：

   1. （随机）选择一个初始值$w^0$。注意，现在确实有研究怎么样选择这个初始值会更好，但是我们这里先不关注这些，即假装不存在这些选择初始值的方法，我们就是随机选择一个初始值。

      

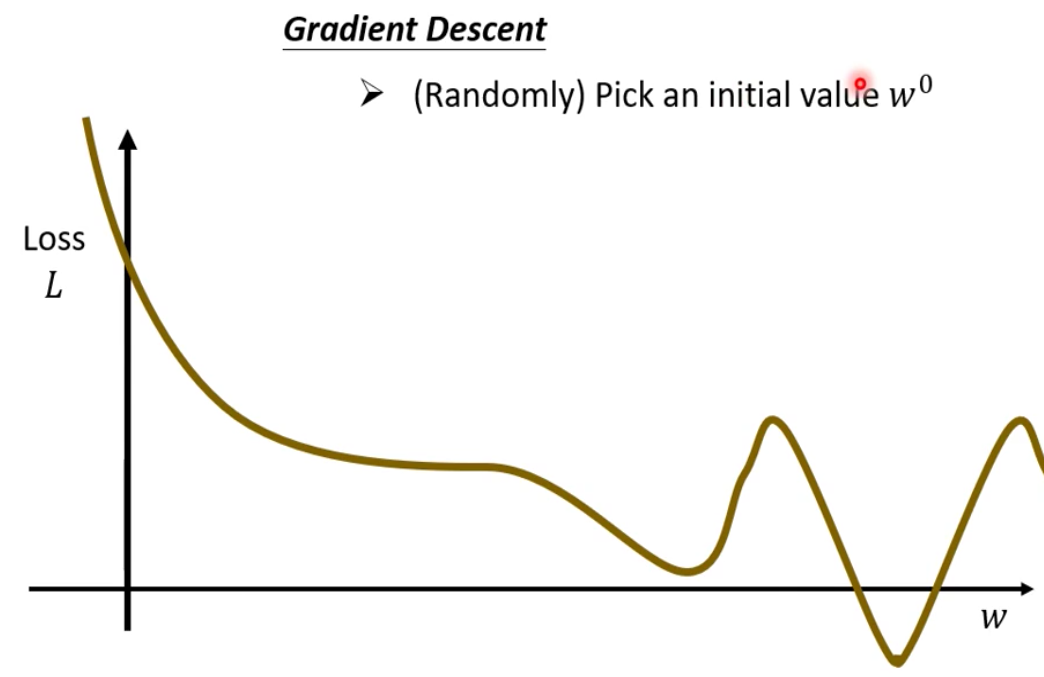
   2. 接下来我们计算Loss对w的微分$\frac{\partial L}{\partial w}|_{w=w^0}$ ，即曲线的斜率

      

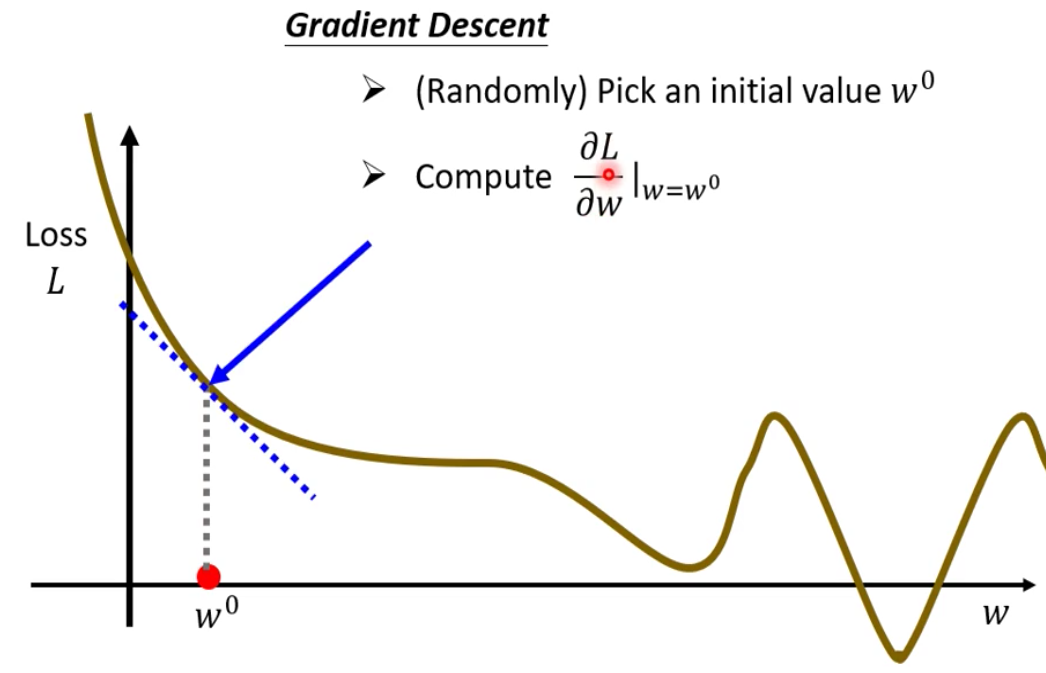
   3. 如果曲线的斜率是负的，那就表示Loss曲线左边高右边低；反之如果曲线的斜率是正的，那就表示Loss曲线右边高左边低。为了能够达到较低的Loss，我们的模型就应该往Loss曲线上低的地方去。

      

      那在前进的时候就会有一个问题，就是到底该前进（下降）多少。由于我们无法控制求导得到的值的大小，因此我们引入一个参数$\eta$来控制下降的多少。这个参数$\eta$称为学习率。由于$\eta$使我们事先设定的，机器没有办法学习这样的参数，因此我们称这些需要自己设定的参数为超参数，Hyperparameter

      

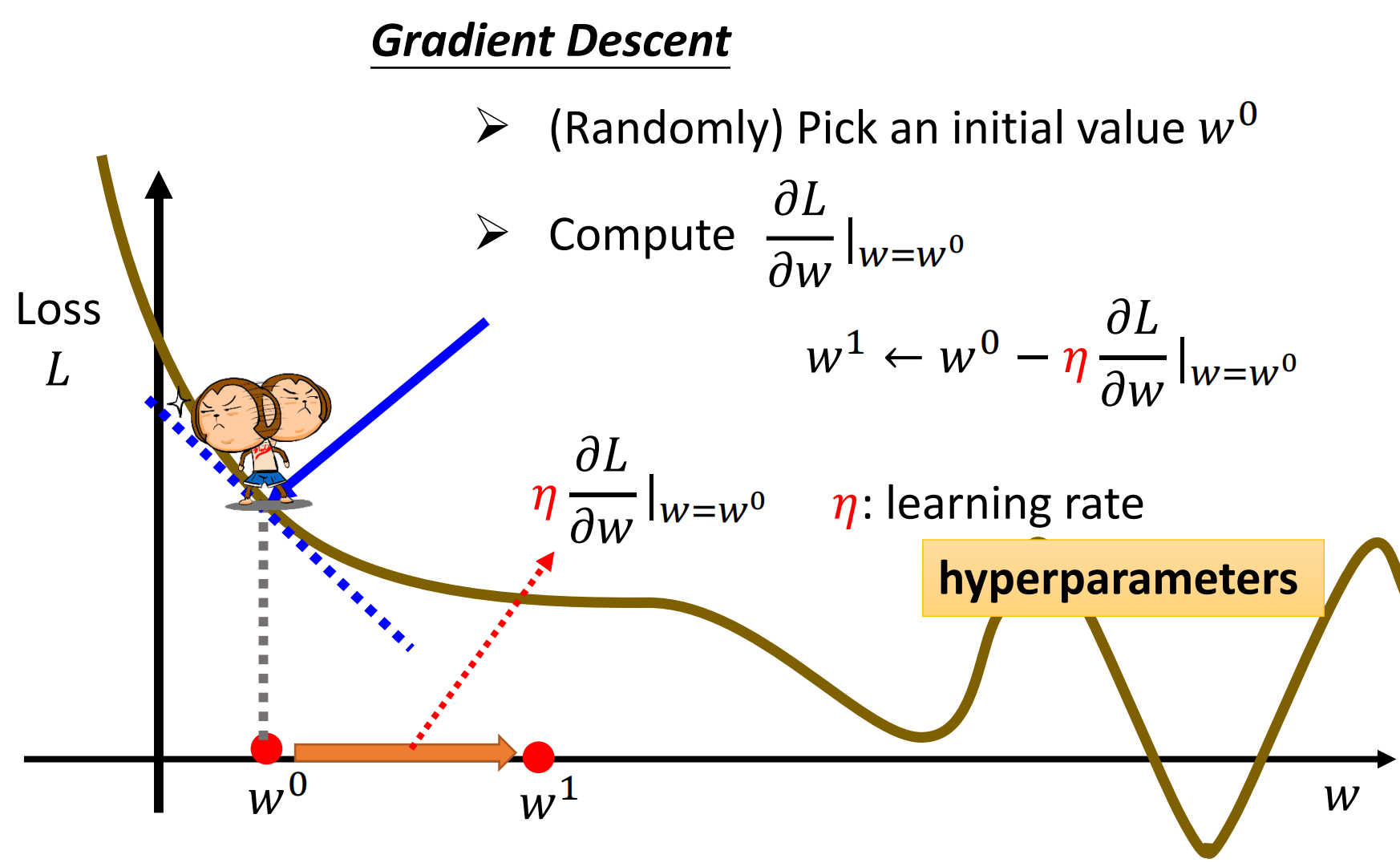
      接下来我们要做的事情，就是重复梯度下降的过程，不断地更新$w$的值。直到最后求到的梯度为0，这样无论$\eta$怎样的变都没有办法继续下降。

      然而使用梯度下降有一个很大的问题就是我们没有找到真正最好的解。我们只会找到一次次好的值。我们称全局最好的值为global minima而局部最小的值为local minima。

      因此就会有人说，深度学习使用梯度下降的一个缺点就是会卡在Local Minima。当然，现在有一些研究就是对梯度下降进行了优化，使得其具有避免卡在local minima的能力

      

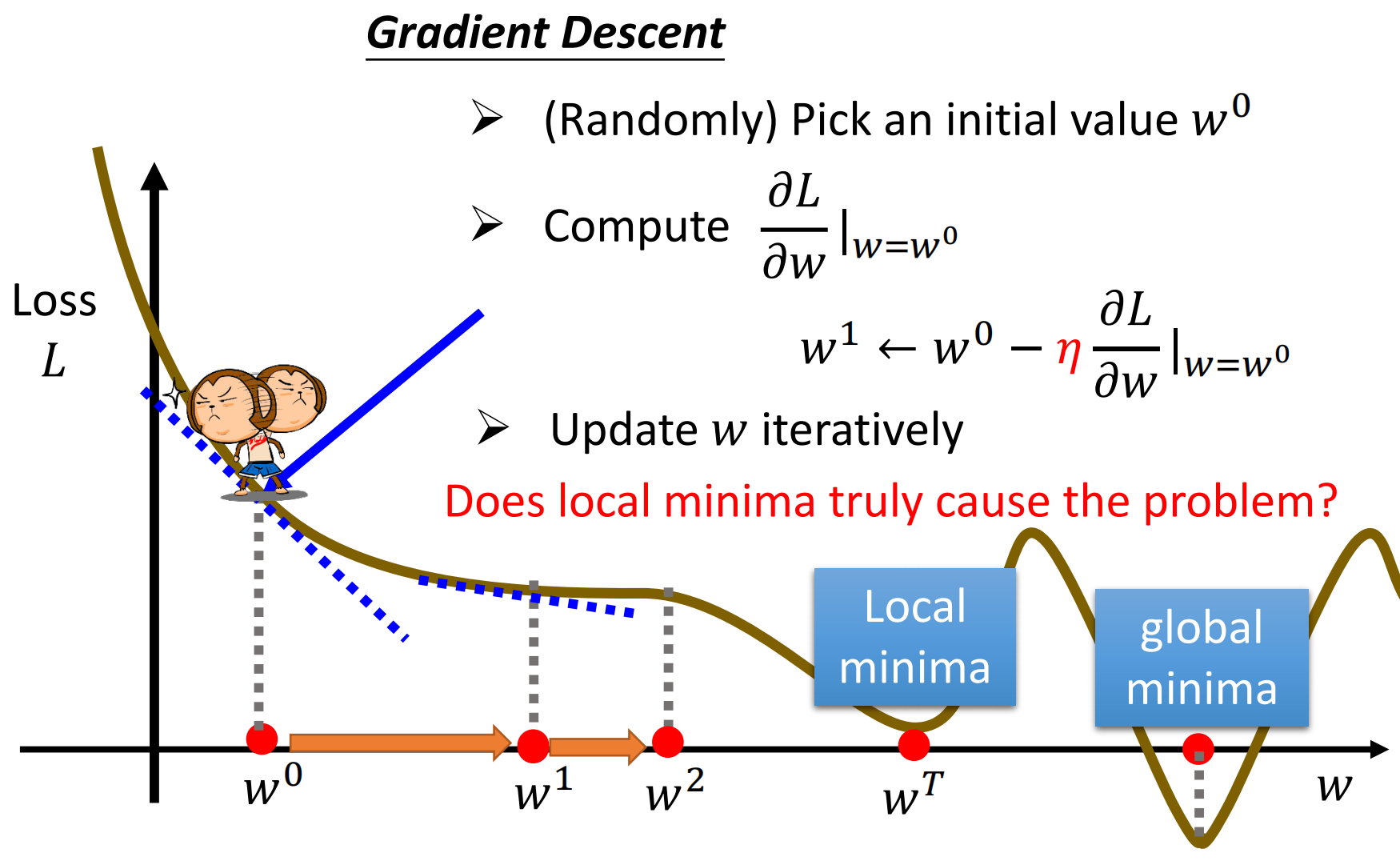
      上面我们是只给出了单变量$w$的优化，下面我们给出两个变量的优化

      

      在刚才的loss surface上，我们整个的优化过程为

      

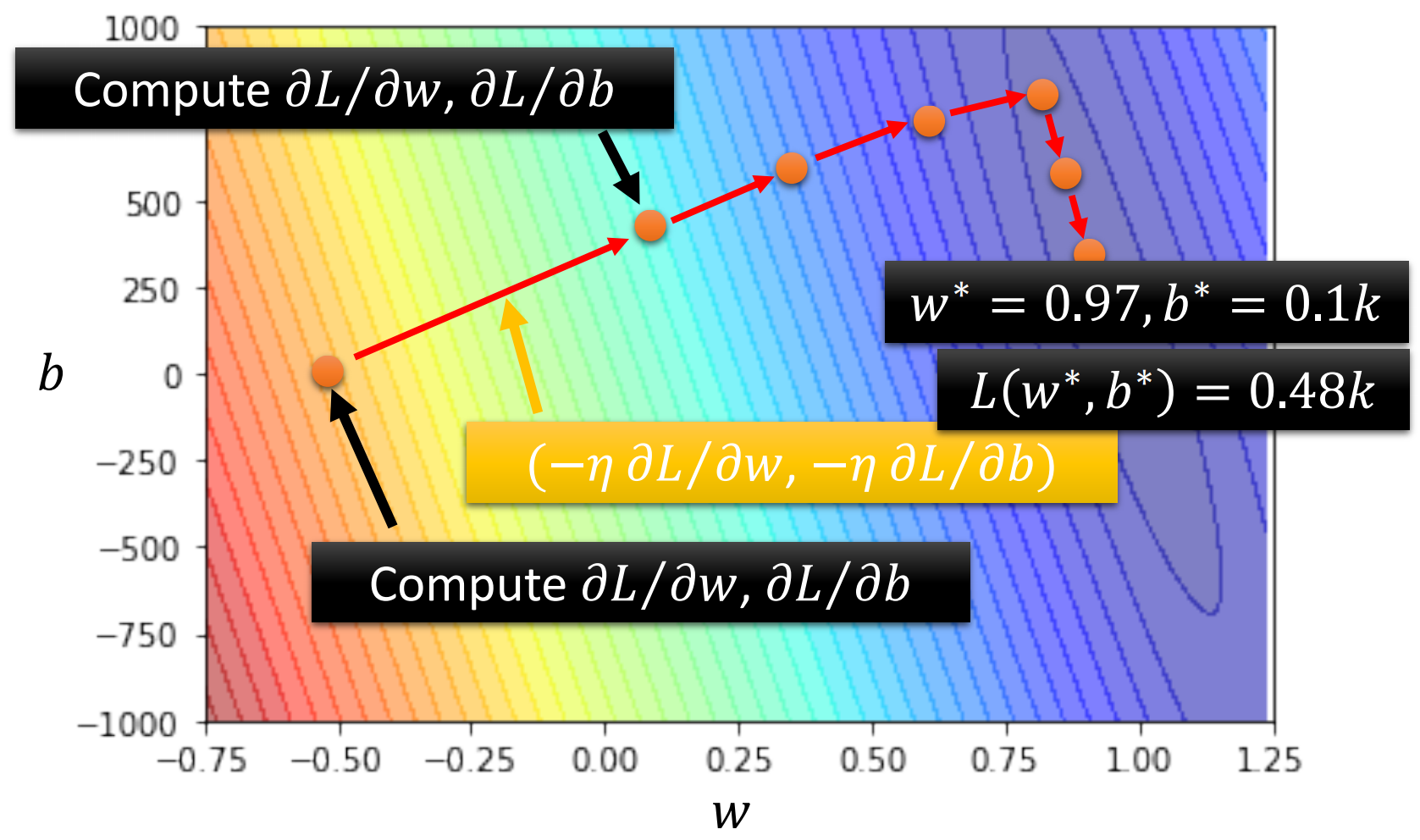
最后通过上面的三步：

1. 根据Domain Knowledge猜测函数的形式（构建模型）
2. 定义loss function
3. 利用Gradient Descent进行优化

我们就找到了最佳的函数。这三步就像把大象放进冰箱里去一样。

最后我们需要注意的是，在上面的这个case中，我们的loss的最佳值是0，而模型其实训练到最后都没有达到最佳的loss，这个时候其实就是我们的模型的极限只能到这里了，这就是我们 $y=b+wx_1$这个model 的 bias。想要进一步的提升我们的模型，就需要通过我们的Domain Knowledge来设计更好地和函数。

C. Training and Testing

我们前面的三步加在一起，称为Training。在Training阶段我们通过训练得到了最优的解。

然而有一个问题就是这些解真的是最优解么？答案其实并不是。因为我们现在的阶段是Training阶段，我们其实是在已经知道答案的数据上计算loss。我们这里只是在自嗨而已，我们假装不知道第二天的观看次数然后预测完了之后进行计算。

而我们真正关心的，应该是在我们不知道答案的数据上，模型也能给出这么好的结果。因此我们接下来要做的，就是用这个函数真的来进行预测。即我们在2020年末用新的数据来预测2021年的观看人数。最后，真实带入进去计算之后得到的在真实的不知道答案的数据上，跑下来的结果是Loss等于0.58

4. Linear Models

正如前面所说，我们的模型在训练阶段得到了模型之后要在测试阶段用从来没有见过的数据（不在测试集中的数据）验证一下看看模型的效果如何。那么上面的线性模型跑下来的结果就如下图

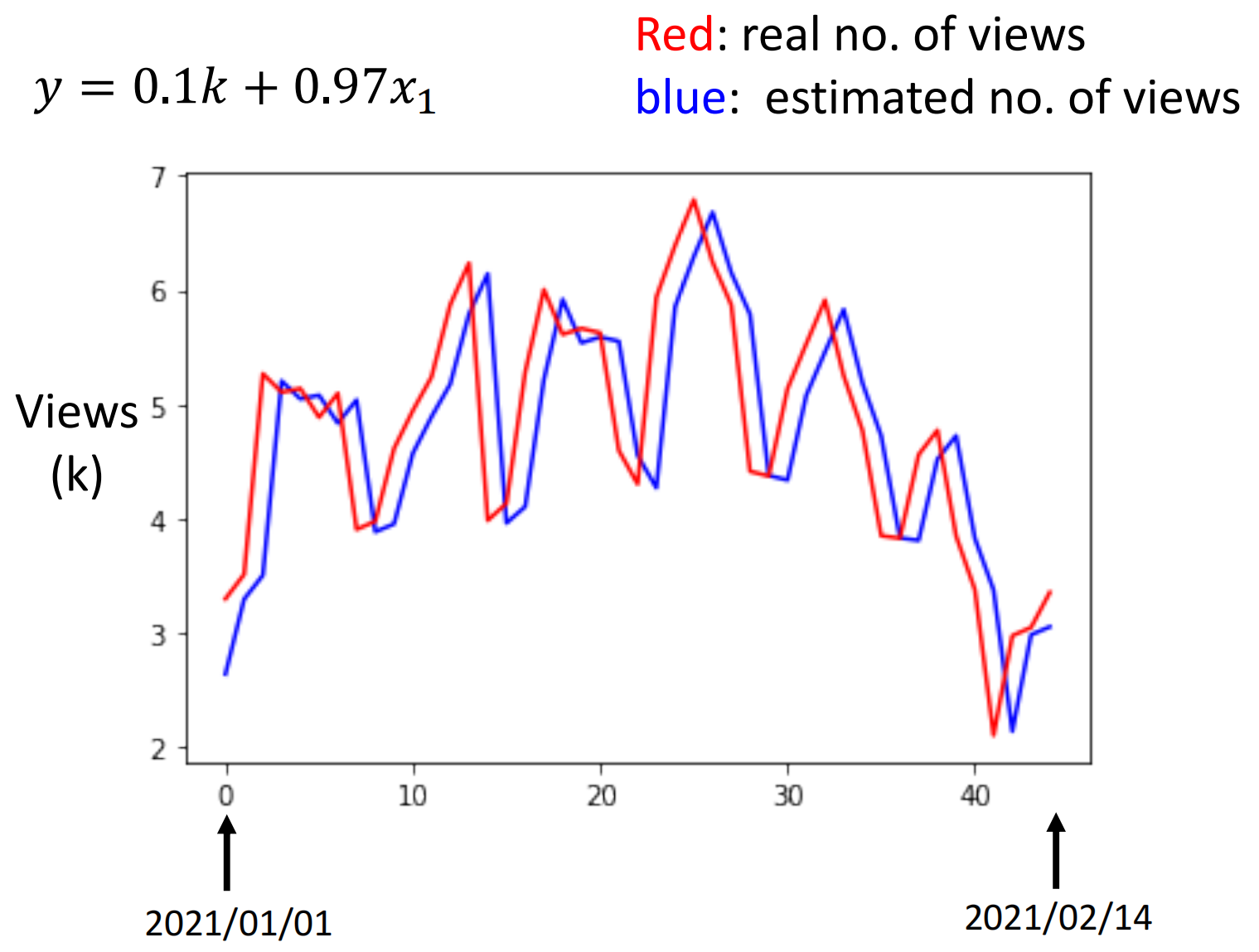
每天观看的矢量基本上就在4~5k左右，而预测的误差达到了0.58k，即平均每天差了600多人次，误差大概20%左右。

此外，我们可以看到，蓝色的线基本上就是红色的线向右平移过去了而已。这就意味着机器的预测基本上就是把前一天的拿来作为第二天的预测。

此外，从红色的真实曲线上，我们其实也能够从中得到一些新的“知识“：

• 观看的人数的涨跌具有周期性。每个七天都会有两天观看人数很低。这两天对应的就是周五和周六。周末毕竟大家都不想学习，所以已能够理解

因此在我们通过对原始数据的观察之后，我们有了新的Domain Knowledge，因此根据新的Domain Knowledge，我们向能不能让模型每次预测下一天的时候都会看看前面几天的数据？这样的话模型就有可能学到当前是周几，然后就会有更好的表现。

退一万步来讲，模型直接把前七天的数据复制过来作为预测也是未尝不可的，也许会预测的更准说不定。

因此，我们现在新的模型如下

$$y=b+\sum_{j=1}^7w_jx_j$$

其中，$j$表示几天前。

那么新的模型训练之后在预测集上进行预测，确实发现我们的性能有了不错的提升

由于我们考虑了前七天的数据，因此我们会有七个$w_j$的值，计算下来具体的结果如下：

类似的，我们就想模型既然看了前七天的数据，他的性能有所提升，那么如果模型看了前一个月的数据呢？因此，我们可以修改我们的模型为

$$y=b+\sum_{j=1}^{28}w_jx_j$$

最后训练下来的结果，确实看了前一个月数据的模型的性能还会有所提升

我们更进一步，让模型看一下前两个月的数据，即

$$y=b+\sum_{j=1}^{56}w_jx_j$$

可是这个时候尽管在训练集上模型的精度有所提升，但是在没有见过的数据（测试集）上，模型的精度并没有提升

那么这就意味着，考虑天数的这个模型已经到了其极限了。

上面的，给feature直接乘以一个数值然后再加上一个数值的模型，我们称为Linear Model

5. From Linear Model to New Model

A. Limited Linear Model

在上面，我们其实已经将Linear的Model发挥到了极限。然而即便如此，每天还是有500多人数的预测的误差，因此我们就像能不能进一步提升我们的模型。

一个合理的质疑就是Linear的Model是不是太简单了？

为什么这样说呢？我们其实可以想象得到，$x_1$和$y$之间可能具有复杂的关系，例如下图的红线。而Linear的Model不管怎么样的改变$w$和$b$，都只能改变直线的倾斜程度和与$y$轴的截距，无法从根本上改变线型。即第二天的观看人数一定前一天的观看人数越多，第二天的观看人数越多/少。

然而就像红色的线，有可能前一天看得人多过了某一个程度之后，第二天看的人就越少。然而对于Linear的Model而言，不管怎么样的改变$w$和$b$，都无法产生红色的线。

因此Linear的Model有很大的limitation。这种来自于Model的限制，称为Model的Bias。即Model能力的上限。

为此，我们就需要一个更加有弹性的，上限更高的一个Model。

B. Synthesis of Piecewise-Curve

为了产生红色这样的曲线，我们其实可以用一个常数再加上一群不同的蓝色的函数来得到上面红色的曲线。蓝色的函数在输入的值很大或者很小的时候都是一个常数，只有值在中间恰好的时候是Slope。

下面蓝色的函数其实有自己专有的名字，但是我们现在先称呼他为一个“蓝方 ”

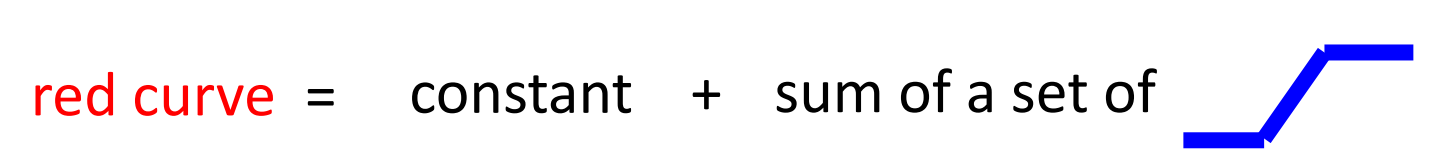
那么首先这个常数项，我们可以通过红方和$y$轴的交点获得

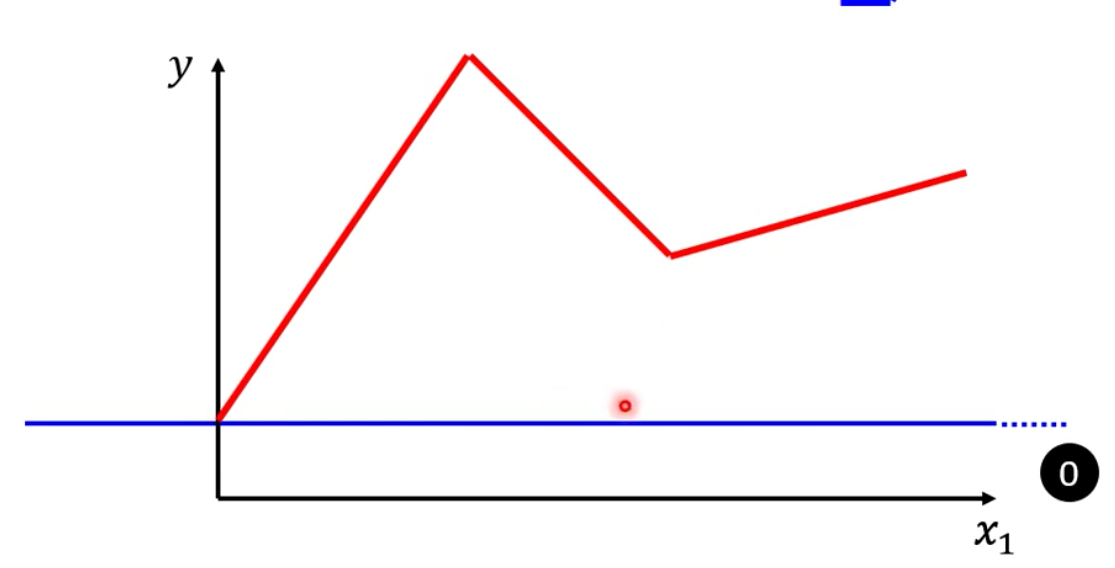
那么要怎么样加上蓝方才能够得到红方呢？我们首先可以这样加：我们让1号蓝方的slope的起点设在红方的第一个拐点，终点设在红方的第二个拐点，并且保持坡度一样。那么这样，1号、2号蓝方相加，就可以得到红方第二个拐点前的部分

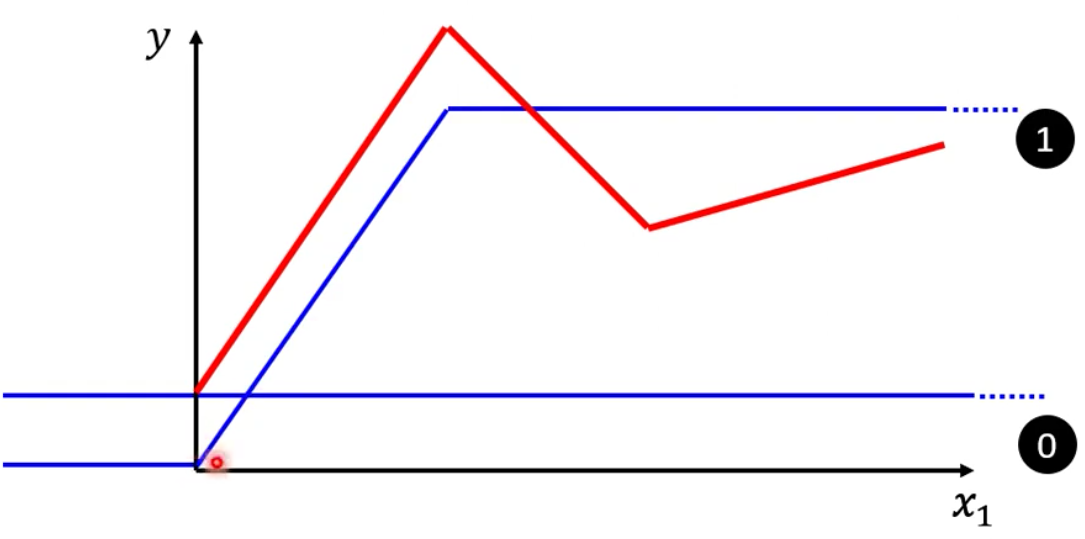
接下来如法炮制，加上第二个蓝方，就可以得到红方的第二段曲线

接下来，红方的最后一段，就用第三个蓝方来合成

最后，我们把0、1、2、3个蓝方相加，就可以得到红方。

其实对于所有的Piecewise的Cureve，都能够通过蓝方来合成，例如下面的一些Piecewise的红方，只是不同的Piecewise的红方需要不同的数量、不同形状的蓝方。通常而言，越复杂的Piecewise的红方需要的蓝方就越多

Piecewise的curve指的是由线段所组成的Curve

C. Beyond Piecewise Curve

在我们日常中，我们其实更常见的函数并不是Piecewise的曲线，而是光滑的、没有间断点的函数，例如下面的函数。但是我们的蓝方函数都是合成有间断点的Piecewise的曲线。

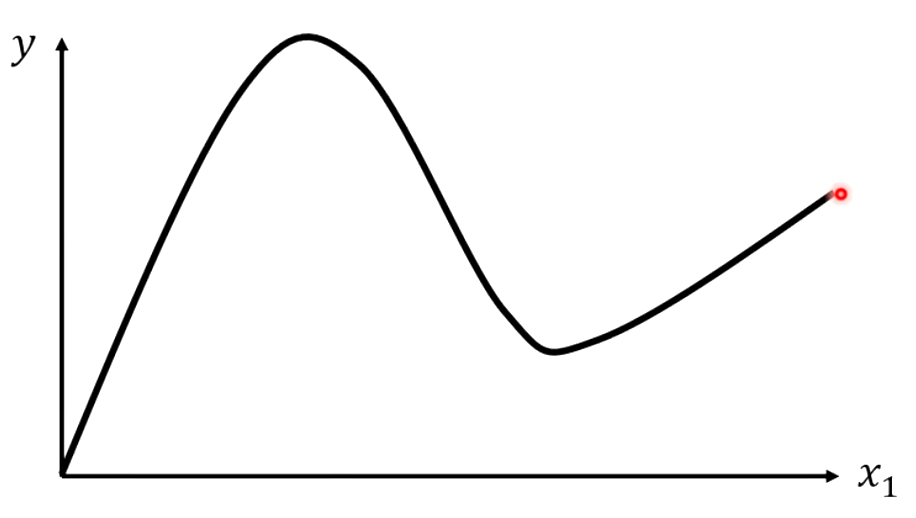
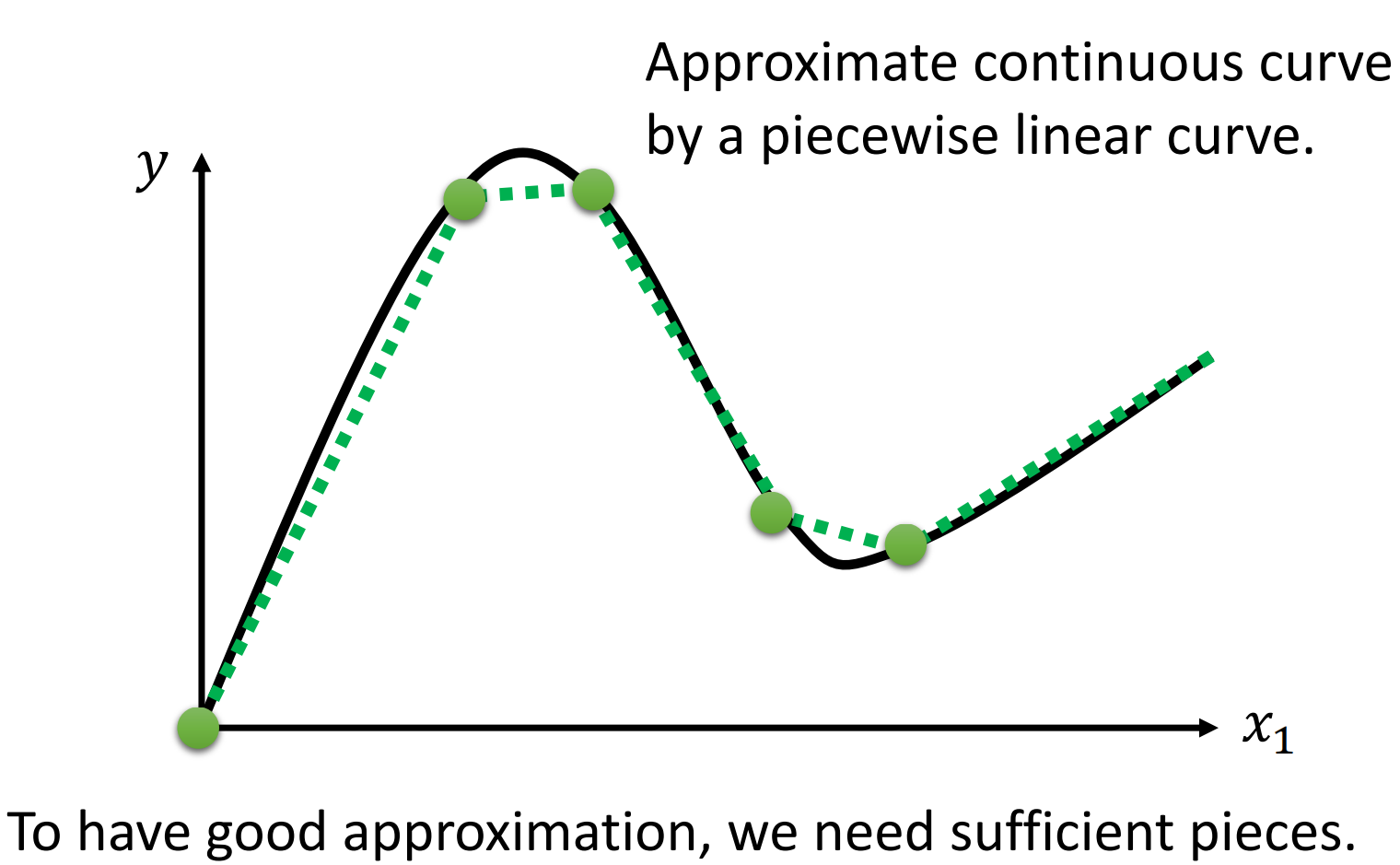
其实问题也不大，我们主需要在连续的光滑曲线上取有点即可，只要我们取的点越多，就越接近原来的光滑函数，拟合的结果就越好。

因此，只要我们取的点够多、取的点位置适当，我们就可以逼近这条不是Piecewise的曲线。因此，我们实际上可以用足够多的蓝方来拟合任意的曲线

D. From Hard to Soft

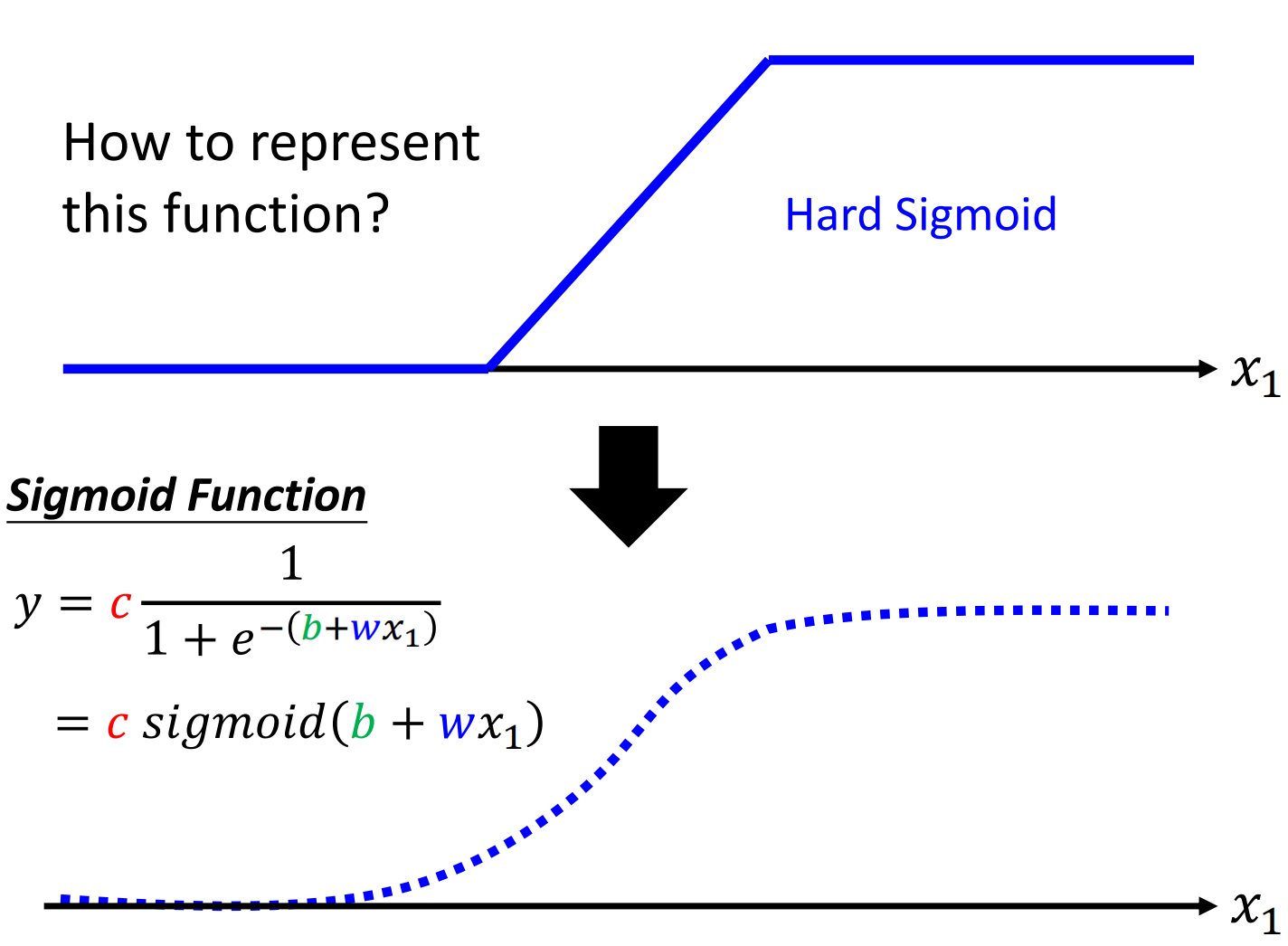
我们就是要写出来蓝方的表达式。因为上面的蓝方我们给的是分段的函数，并且由于在拟合的时候不同的蓝方需要的开始转折的$x$的不同，因此比较难写出来蓝方的表达式。而且在计算的时候由于分段会导致条件比较，因此就是用一条曲线来逼近、表示蓝方。

用于逼近蓝方的曲线就叫做$Sigmoid$函数，其表达式如下

$$y=c\frac 1{1+e^{-(b+wx_1)}}=csigmoid(b+wx_1)$$

Sigmoid和蓝方非常相近，在$x$很大或者很小的时候，$y$都是常数，在中间是非线性的上升。

Sigmoid如果要翻译中文，可以是S型曲线。

其实在历史上，是先出现了Sigmoid函数才出现了我们上面的蓝方，不过为了方便讲解，因此我们先介绍的蓝方再介绍的Sigmoid函数。所以上面一直再说的蓝方，其实称为Hard Sigmoid

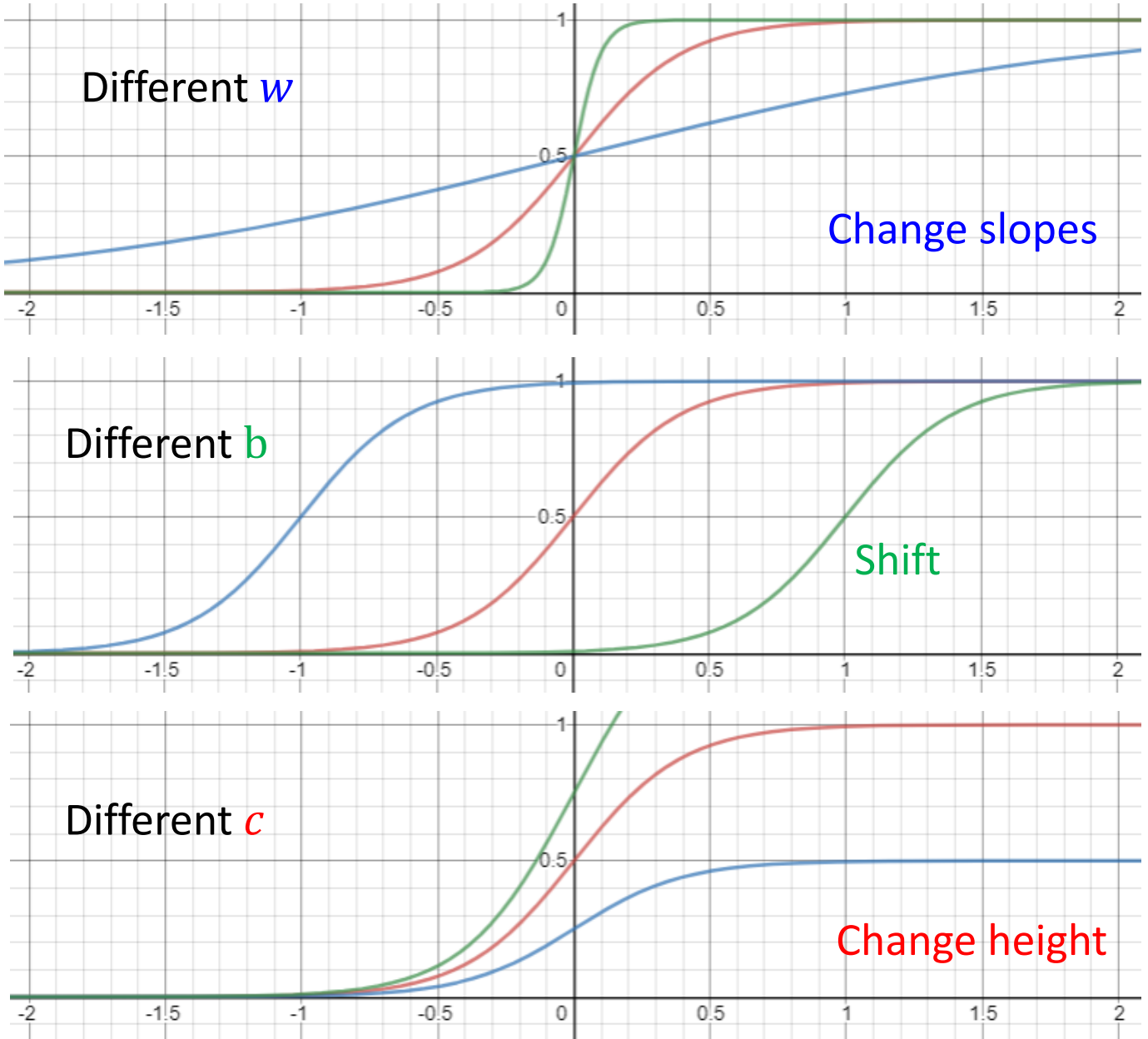
那么还有一个问题，就是我们上面的蓝方的slope是可以左右平移的，那么Sigmoid又该如何去平移呢？

事实上，我们改变Sigmoid中的$c$、$b$、$w$即可制造出不同的Sigmoid函数。而有了不同的Sigmoid函数之后，我们叠加起来就可以去逼近不同的Piecewise的曲线，而Piecewise的曲线又可以去逼近各种各样光滑的曲线

所以对于上面的红方，我们就可以用几个Sigmoid来逼近

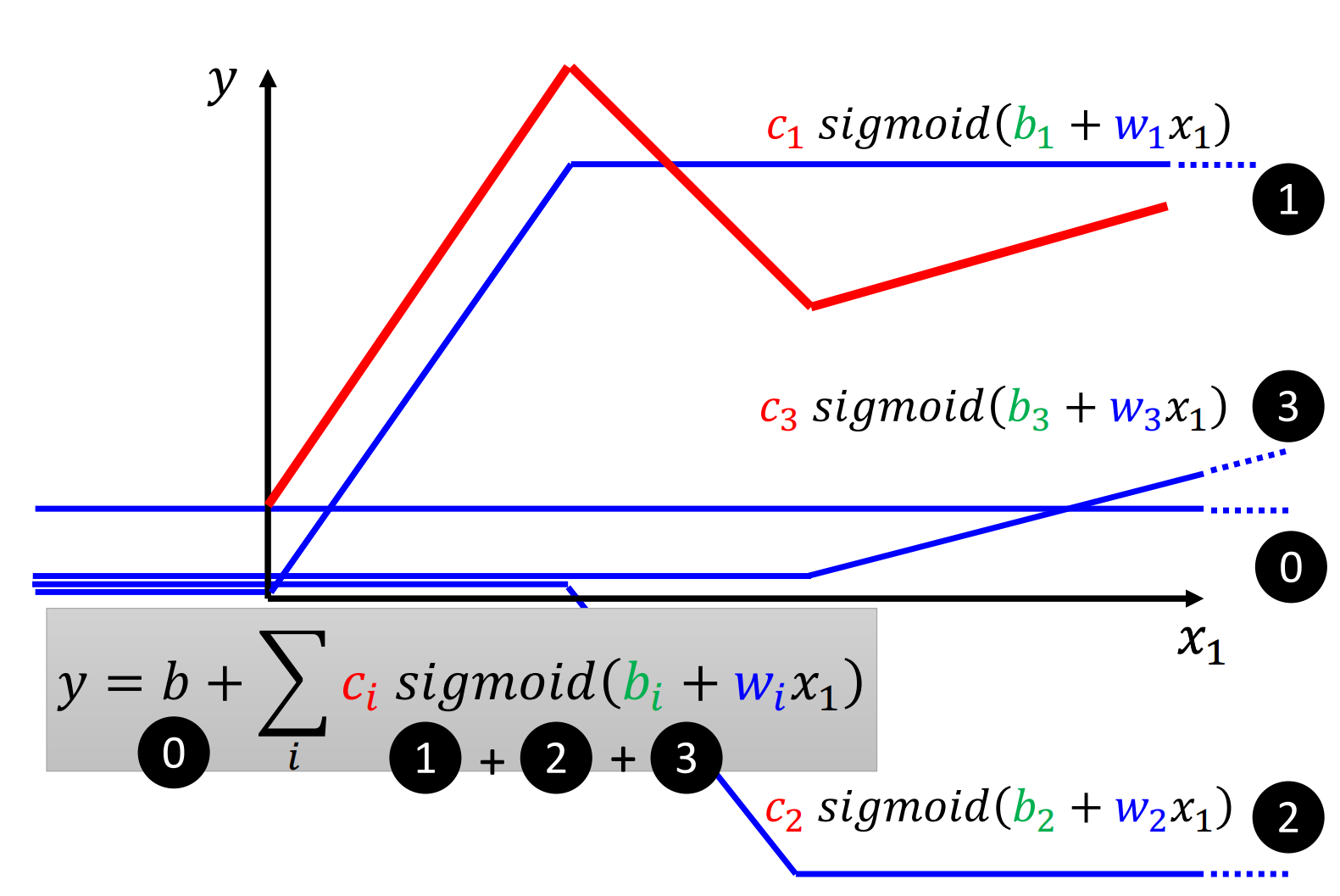
E. From Linear to New Model

总结一下上面，由于Linear Model存在非常大的Model Bias，而我们首先通过Hard Sigmoid来拟合任意的函数，最后用Sigmoid来拟合Hard Sigmoid。所以我们现在就获得了一个更加flexible的model

那么其实，$y=b+wx_1$这个并不是我们表现最好的Linear Model，上面我们的最好的Linear Model是看多个feature的Linear Model，即

$$y=b+\sum_{j=1}^nw_jx_j$$

那么我们现在要把这个Linear的Model扩展成Sigmoid这种Model的话，只需要把Sigmoid里面的东西换掉即可，则式子如下：

上面的这个如果看起来头痛的话，我们用更直观的方式把他来画出来。我们现在先假设$j=1,2,3$，即只有三个Feature，模型只会看前三天的观看人数。我们还假设$i=1,2,3$，即我们用三个Sigmoid Function来拟合曲线。

那么我们首先先画出来输入

然后我们再画出来三个Sigmoid函数，一个黑色的圆圈表示一个Sigmoid函数，由于我们有三个Sigmoid函数，因此就有三个黑色的圆圈

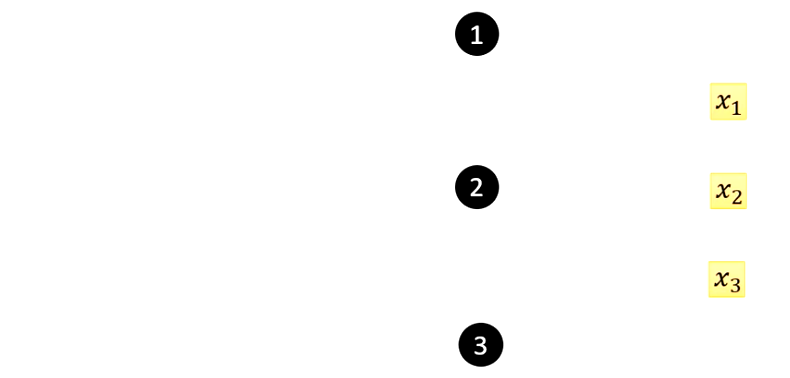
画完了基础的元素之后，我们就开始画出来运算的步骤。

我们首先看要怎么样画出来Sigmoid内部括号里的东西。括号里的东西就是给每个$x$乘以一个数字$w$，然后再把三者相加，最后加一个$b$，所以我们下面这样画括号内部的东西

同理，我们画出来第二个、第三个Sigmoid函数，我们就不写出来所有的$w$了，那么最后画下来的结果如下图

为了简单期间，我们把每个括号内计算的结果记为$r$，那么最后的结果就是

我们把上面三个括号的式子向量化，用矩阵乘法的形式来表达，就有向量$\vec x$乘以一个矩阵$W$在加上一个向量$\vec b$就得到了一个向量$\vec r$

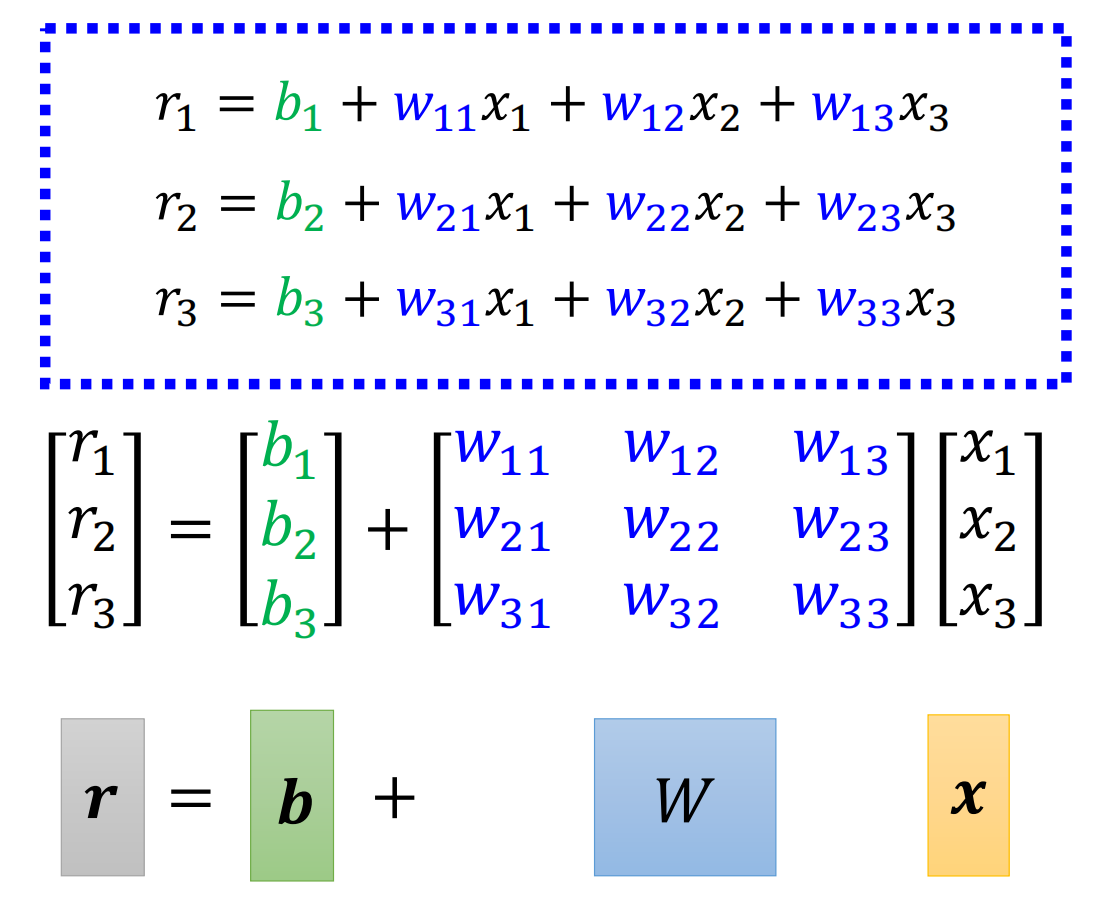
所以括号里干事事情就是下面的图

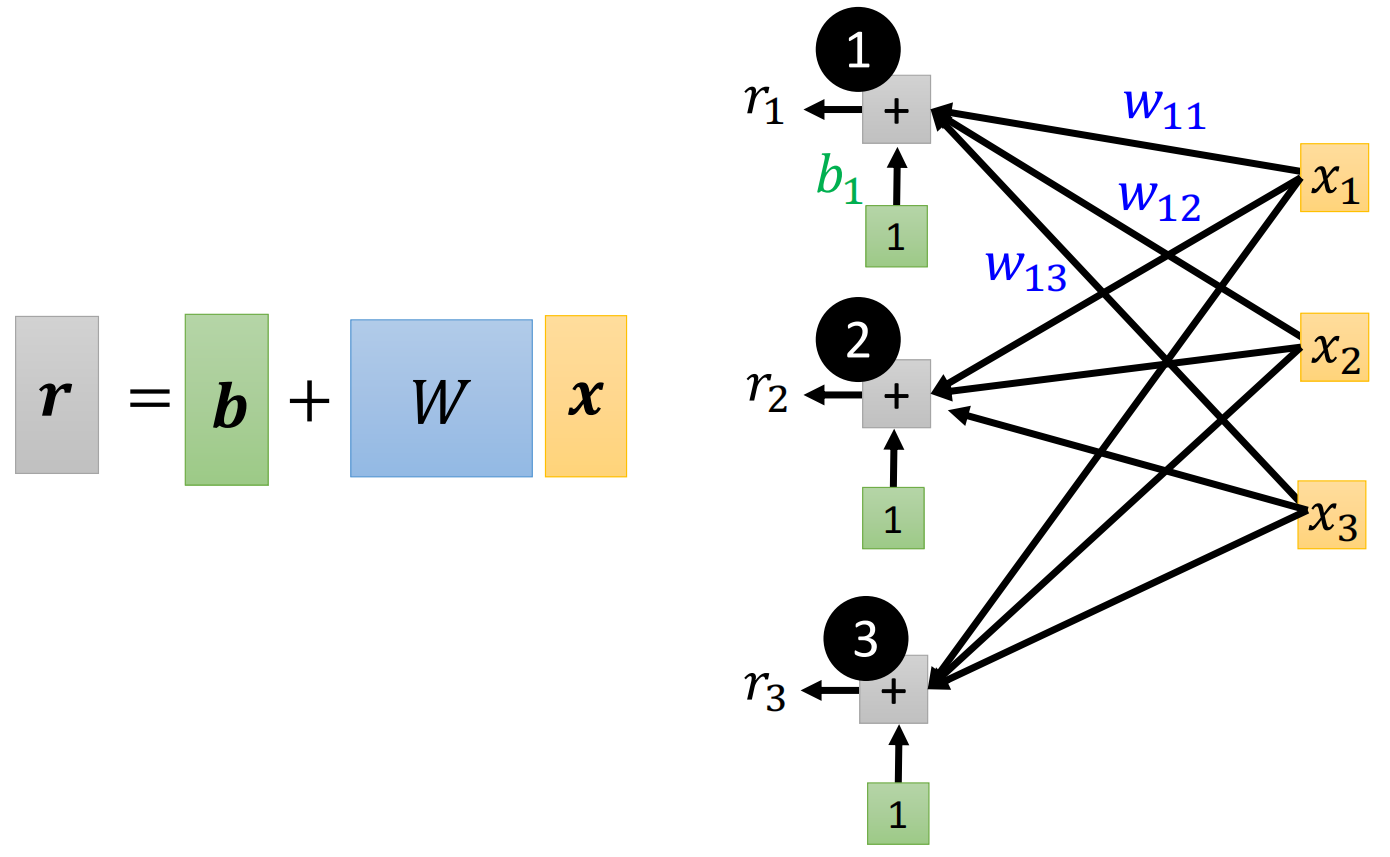
接下来，赛算完括号里的东西后，要通过Sigmoid函数，所以三个$r$要分别通过三个Sigmoid函数。我们同样简写一下，用一个小写的希腊字母sigma来表示Sigmoid函数，即

$$\begin{cases} a_1=sigmiod(r_1)\\ a_2=sigmiod(r_2)\\ a_3=sigmiod(r_3) \end{cases} \Leftrightarrow \vec a = \sigma(\vec r)$$

我们最后一步，就是把三个$a$再用一个Linear Model，即乘以权重再相加，用矩阵表示，就是

$$y=\vec b + {\vec c^T} \vec a$$

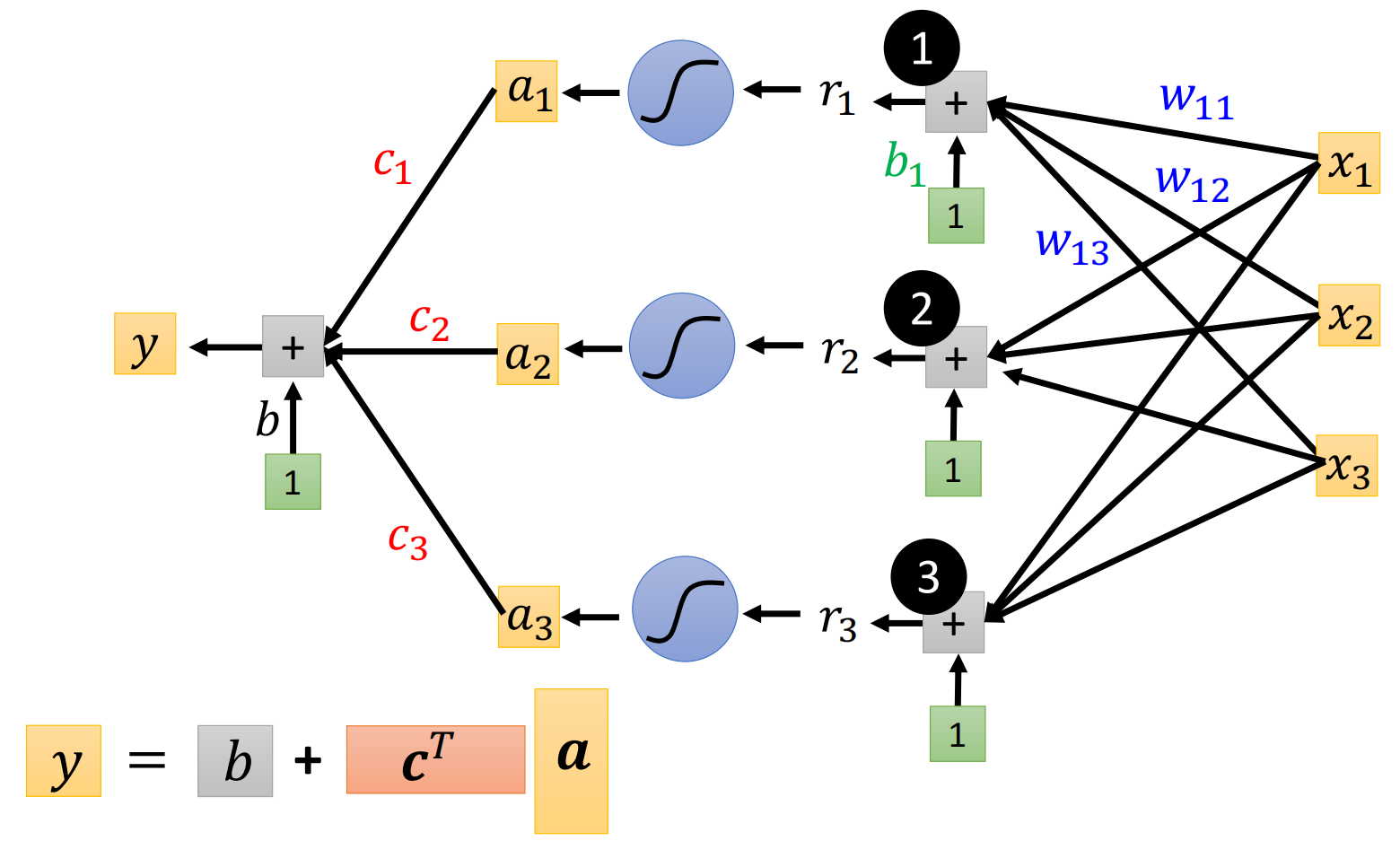
所以我们上面一连串的运算，用矩阵表示出来就是

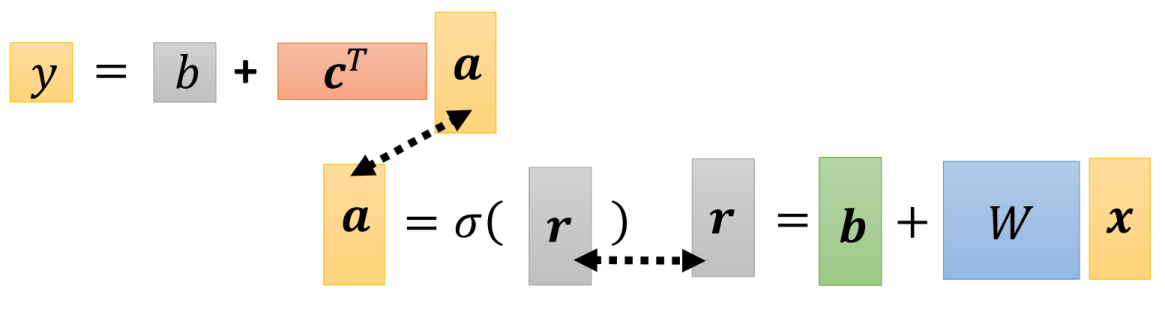
最后，我们用一个式子表示就是

上面就是我们得到的New Model

6. New Model

上面我们通过Linear的Model不断深入，得到了New Model。那么我们下面就将聚焦于New Model的优化

A. Model Parameter / Function with Unknow Parameter

我们在前面说过，机器学习的模型其实都是带有参数的函数，New Model也不例外，例如我们上边的New Model

$$y=b+c^T\sigma(b+Wx)$$

我们先重新定义一下符号。

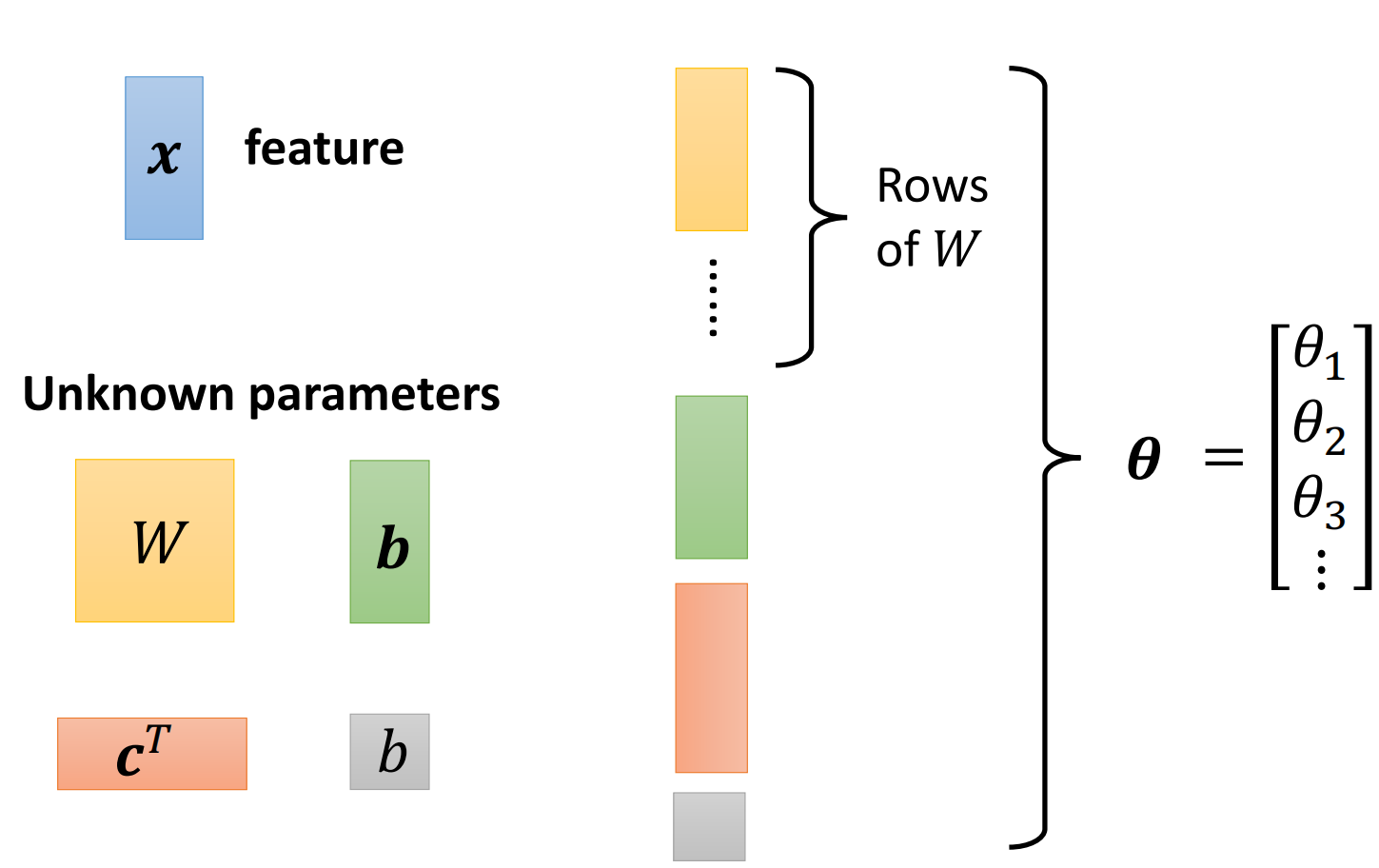
在上式中，$x$称为feature，而所有未知的参数是$W$、$b$、$c$、$b$。注意我们有两个$b$，一个$b$是向量，另外一个是标量

由于$x$是feature，是一开始就给定的，因此我们实际上需要让机器去寻找的参数就是$W$、$b$、$c$、$b$

我们把这四个未知的参数拿出来，拉直，拼成一个很长的向量，我们用$\theta$来表示这个向量，如下图。

那么$\theta$中有一些值来自于W，有一些值来自于$b$，还有一些来自于$c$，我们这里就不去管他们了，把模型中所有未知的参数统称为模型的参数$\theta$

B. Back to ML Framework: Define Loss

我们在前面讲Linear Model的时候，说道：模型就是函数，而机器学习就是让机器去找函数的最佳参数。我们找这个函数的过程包括三步：

1. 定义模型 / 定义参数
2. 定义Loss
3. 使用Gradient Descent来优化参数，找到最佳的参数

那么对于New Model来说，我们上面定义了New Model的含参函数表达式（function with unknown parameter），接下来就到了第二步骤，要定义Loss

我们前面说过，loss function是模型参数的函数，对于Linear的Model来说，$L=L(w,b)$，而对于New Model来说，我们上面已经定义了模型的参数为$\theta$，所以对于神经网络来说，$L=L(\theta)$

而对于Loss具体的计算来说，由于Loss的计算是根据数据定义的，而我们的数据其实没有变，只是变了模型，所以loss function的计算其实没有变，只是符号改变了一下。

我们给定一组参数的值$b,c,b,W$，然后让模型用这套参数给出预测$y$，再和真实的label $\hat y$作比较，计算一个error $e$，最后做平均即可

C. Back to ML Framework: Optimize

在定义完模型和损失函数之后，接下来的一步就是对模型进行优化了。

而对New Model进行Optimization和对Linear的Model进行Optimization的算法是一模一样的，就是Gradient Descent

我们这里的目标就是

$$\theta^* = arg\min_\theta L$$

而

$$\theta = \begin{bmatrix} \theta_1\\ \theta_2\\ \theta_3\\ \vdots \end{bmatrix}$$

那么同样的，我们还是三步走：

1. 首先随机初始化一个$\theta$的初始值$\theta^0$

2. 接下来根据损失函数得到的Loss计算参数的微分，得到g。因为我们的参数是一个向量，所以计算得到的微分也是一个向量，这个微分向量称为Gradient

   $$g=\begin{bmatrix} \frac{\partial L}{\partial \theta_1}|_{\theta=\theta^0}\\ \frac{\partial L}{\partial \theta_2}|_{\theta=\theta^0}\\ \frac{\partial L}{\partial \theta_3}|_{\theta=\theta^0}\\ \frac{\partial L}{\partial \theta_4}|_{\theta=\theta^0}\\ \vdots \end{bmatrix}$$

   上面的式子可以简写为

   $$g=\nabla L(\theta^0)$$

3. 第三步就是利用计算得到的Gradient来更新我们的参数，即

   $$\begin{bmatrix} \theta_1^1\\ \theta_2^1\\ \theta_3^1\\ \vdots \end{bmatrix} \leftarrow \begin{bmatrix} \theta_1^0\\ \theta_2^0\\ \theta_3^0\\ \vdots \end{bmatrix} - \begin{bmatrix} \eta \frac{\partial L}{\partial \theta_1}|_{\theta=\theta^0}\\ \eta \frac{\partial L}{\partial \theta_2}|_{\theta=\theta^0}\\ \eta \frac{\partial L}{\partial \theta_3}|_{\theta=\theta^0}\\ \vdots \end{bmatrix}$$

   简写上面的式子就是

   $$\theta^1\leftarrow \theta^0-\eta g$$

4. 然后重复上面的步骤，不断计算梯度、进行优化，直到我们不想继续算下去或者算出来的Gradient全是0.

   当然在实际上，基本上都是我们不想继续算了，很少会有算到的Gradient全是0

   $$\theta^2\leftarrow \theta^1-\eta g\\ \theta^3\leftarrow \theta^2-\eta g\\ \theta^4\leftarrow \theta^3-\eta g\\ \vdots$$

D. Mini-Batch

上面其实已经介绍完了New Mode的训练。其实在训练过程中还有一个小问题，就是在实际的计算的过程中，我们每次计算梯度并不是直接用所有的数据，而是用所有的数据中的一小部分。

我们用这一小部分数据在一起算一个Loss，然后用这一小部分的数据算到一个Loss $L^1$。然后用这个Loss去算一个梯度$g=\nabla L^1(\theta^0)$

这一小部分数据就称为一个Batch。一个Batch里的数据直接随机抽样就可以得到

然后我们继续取第二个Batch计算、第三个Batch计算……

直到我们用完所有的数据。把所有的Batch都计算过一遍就称为一个epoch

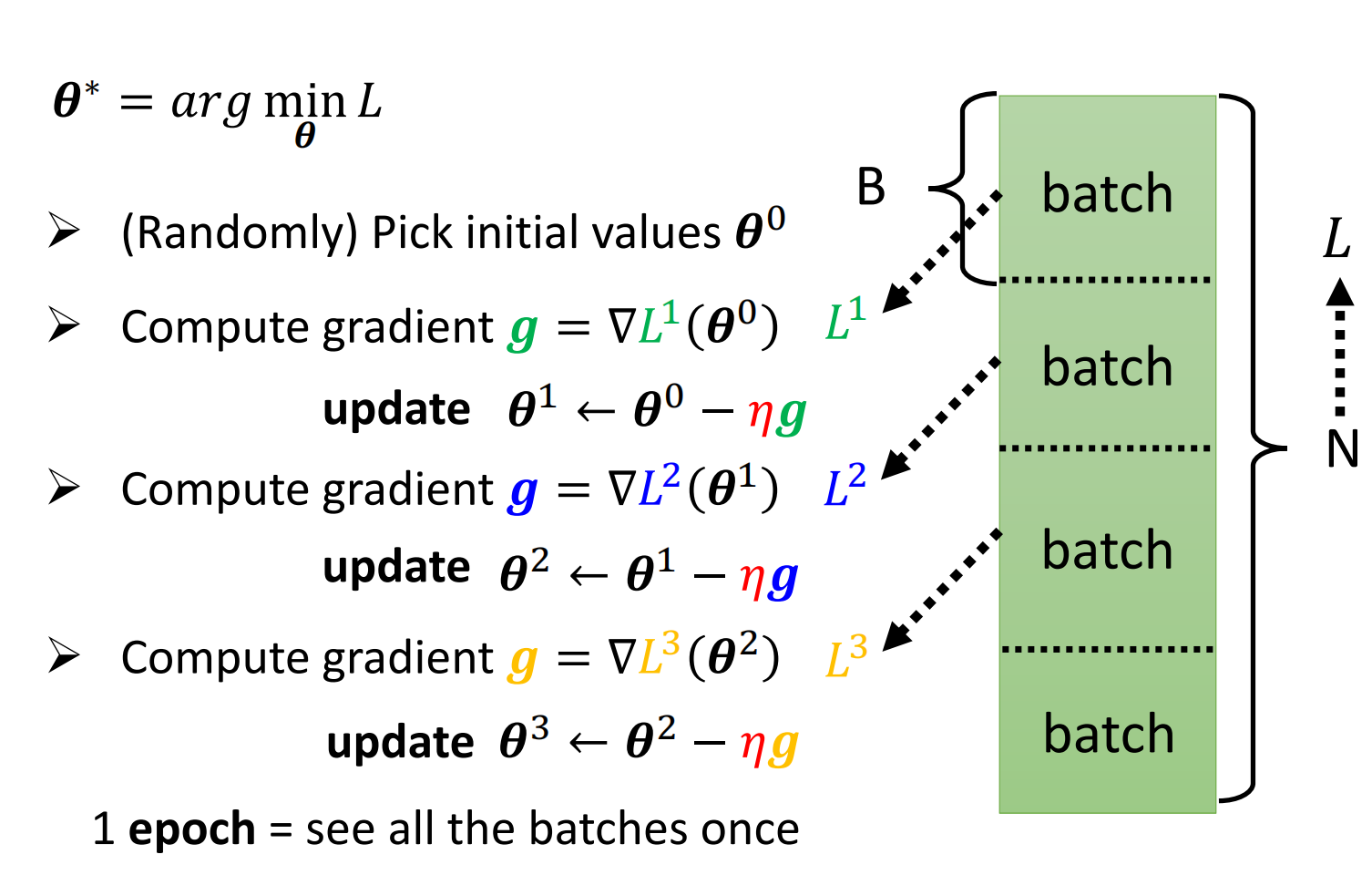
至于为什么要使用Batch？下个文章再说（下节课老师才讲），毕竟这个文章以及有8500字了。

为了加深影响，举两个例子来说，

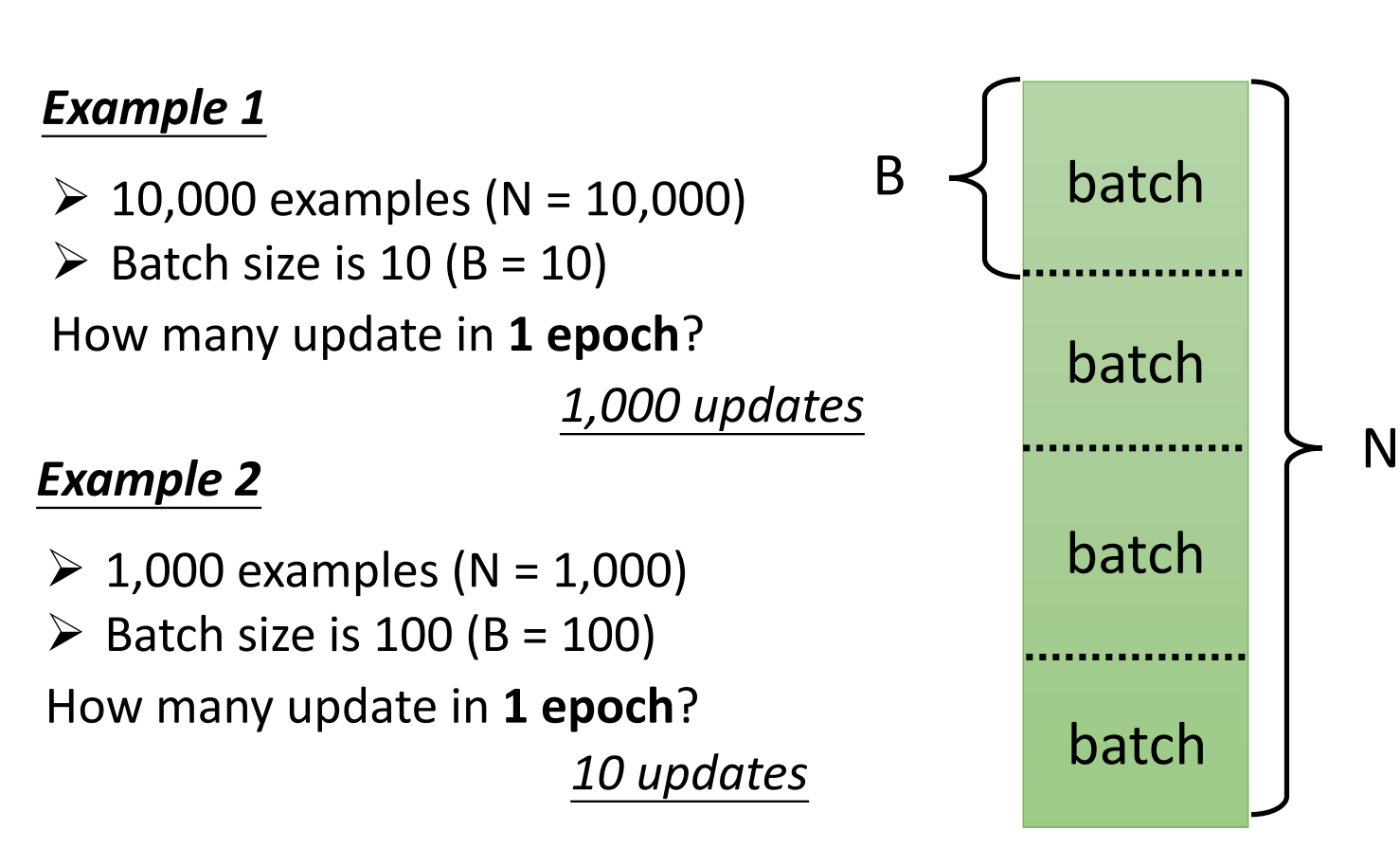
此外，由于Batch的大小也是我们自己定的，因此一个Batch有多少个数据，即Batch Size也是一个由我们决定的Hyper-Parameter

E. ReLu: Rectified Linear Unit (ReLU)

我们其实还可以对模型做更多的变形。例如上面我们是用Sigmoid来替换Hard的Sigmoid。其实我们也可以用别的来代替Sigmoid

例如用下面的函数

$$y=\begin{cases} x, & x> 0\\ 0, & x <0 \end{cases}$$

简写为

$$y=c\max(0, b+wx_1)$$

我们只需要改变$0$、w、$w$、$b$就同样可以实现线的平移。

其实用两个ReLu就可以合成Hard Sigmoid，例如下面的图

所以如果想在模型中使用Hard Sigmoid而非Sigmoid的话，每个Sigmoid用两个Relu代替就行。

类似的，Sigmoid、ReLu、Hard Sigmoid这些函数在神经网络中，我们称其为Activation Function

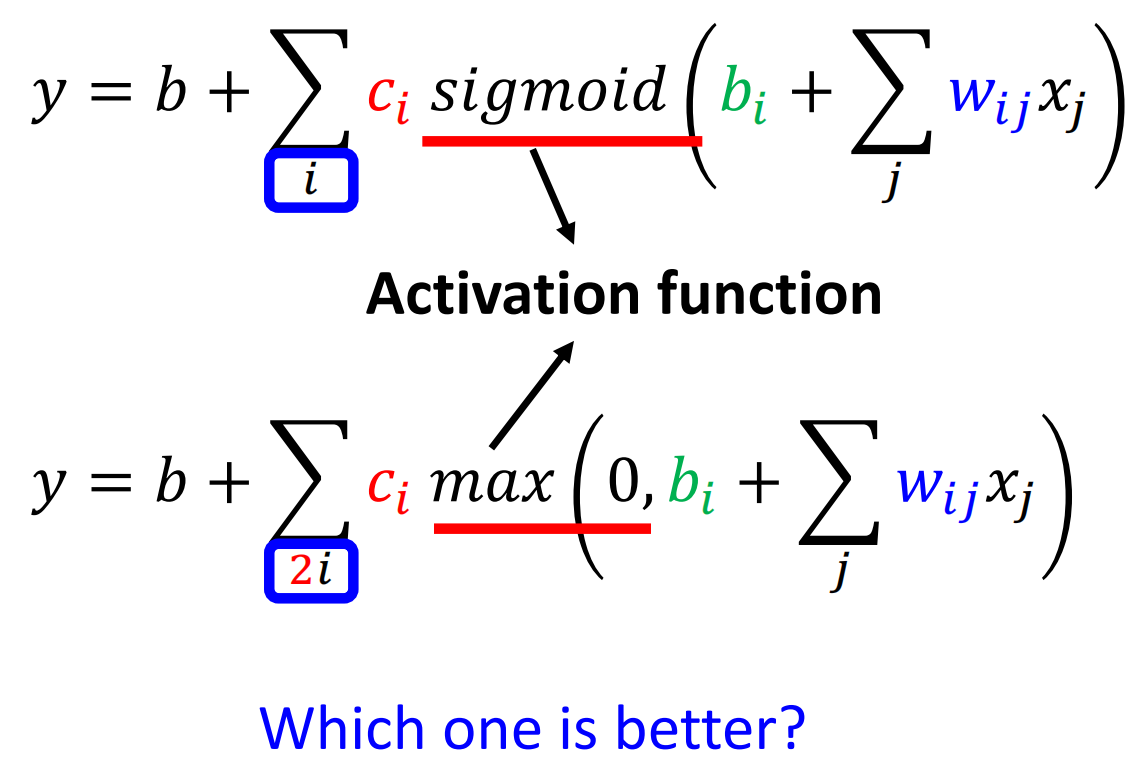
当然，还有其他的Activation Function。至于哪种激活函数比较好呢？下次再讲（写），这里快写不下了

7. Case Study: Neural Network Application

我们上面讲解了新模型的训练，那么接下来就把神经网络运用到上面YouTube观看次数预测的案例中去

A. 单层

我们首先用上面的New Model，表达式如下，然后选用不同的ReLu的数量。

我们可以看到使用了新的模型的性能确实相比于Linear的Model有所提升，但是到了1000个ReLu之后，性能又到了瓶颈

B. 多层

我们上面都是只用了一层的新模型，即只有一层Activation Function。我们其实可以把第一层输出的$a$当做输入的$x$丢给下一层继续去计算

那么通过这样不断地重复，我们就可以获得更深的模型。这里到底要叠多深，也是一个超参数。

我们继续进行实验，每一层用100个ReLu，实验的结果如下

下面就是真实的通过三层ReLu的实验结果

我们能够看到，不断叠深的模型确实学到了周期这个规律，并且大部分时间预测的都很准。

但是还是有一个问题，就在最右边出现了一个低谷，当天机器并没有预测到低谷，而是在第二天才出现了低谷。

那么这一天其实就是过年，这一天是除夕，没人会在除夕学机器学习吧？😂

8. Origin of Name

就像Linear Model一样，我们上面的模型也要有一个名字，毕竟有了一个Fancy的名字才能够吸引人

对于每一个激活函数，我们把他们称为一个Neural，那么整个模型就成为Neural Network

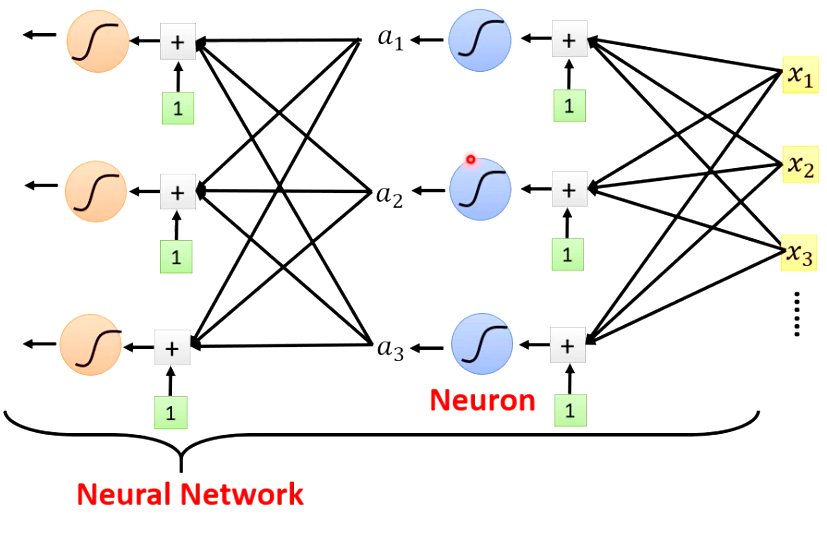
然而Neural Network这个名词在80、90年代其实就已经被玩烂了。那时候的人们对Neural Network的预期很高。可是最后受到当时技术的限制，Neural Network的表现让人大跌眼镜。所以Neural Network的名字就被搞臭掉了。

基本上Paper里有Neural Network，Paper就会被据掉。所以后来，为了重振Neural Network的雄风，就给了Neural Network新的名字。

我们把每一层称为一个Hidden Layer，很多层在一起那就是一个Deep的Network，那么就把这个技术称为Deep Learning。

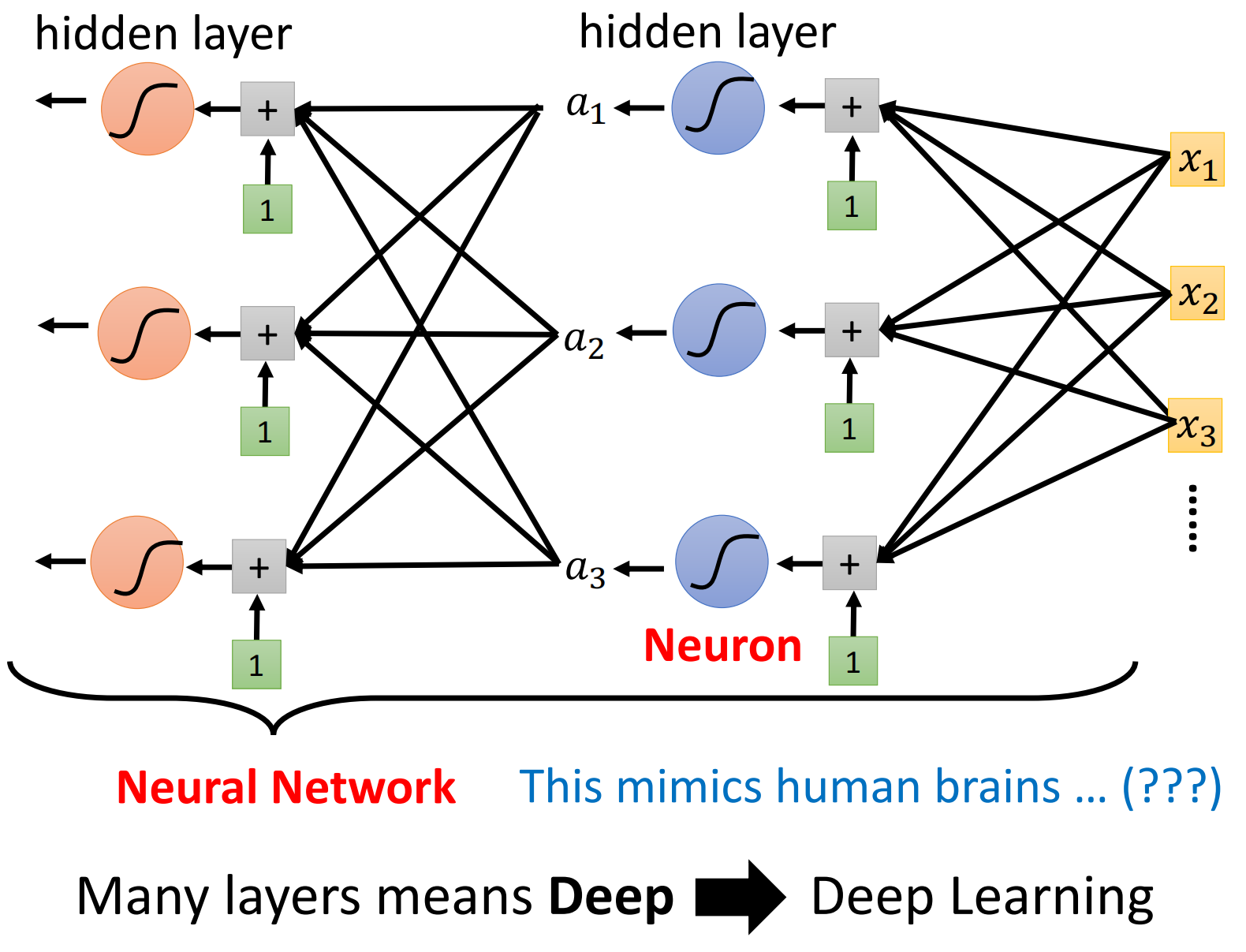
9. Deep Network

后来随着深度学习技术的发展，人们把网络越叠越深，2012年AlexNet有8层，在图像分类上的错误率为16.4%。到了2014年，牛津的VGG叠了19层，错误率为7.3%。在同一年谷歌的GoogleNet叠了22层，错误率降到了6.7%。

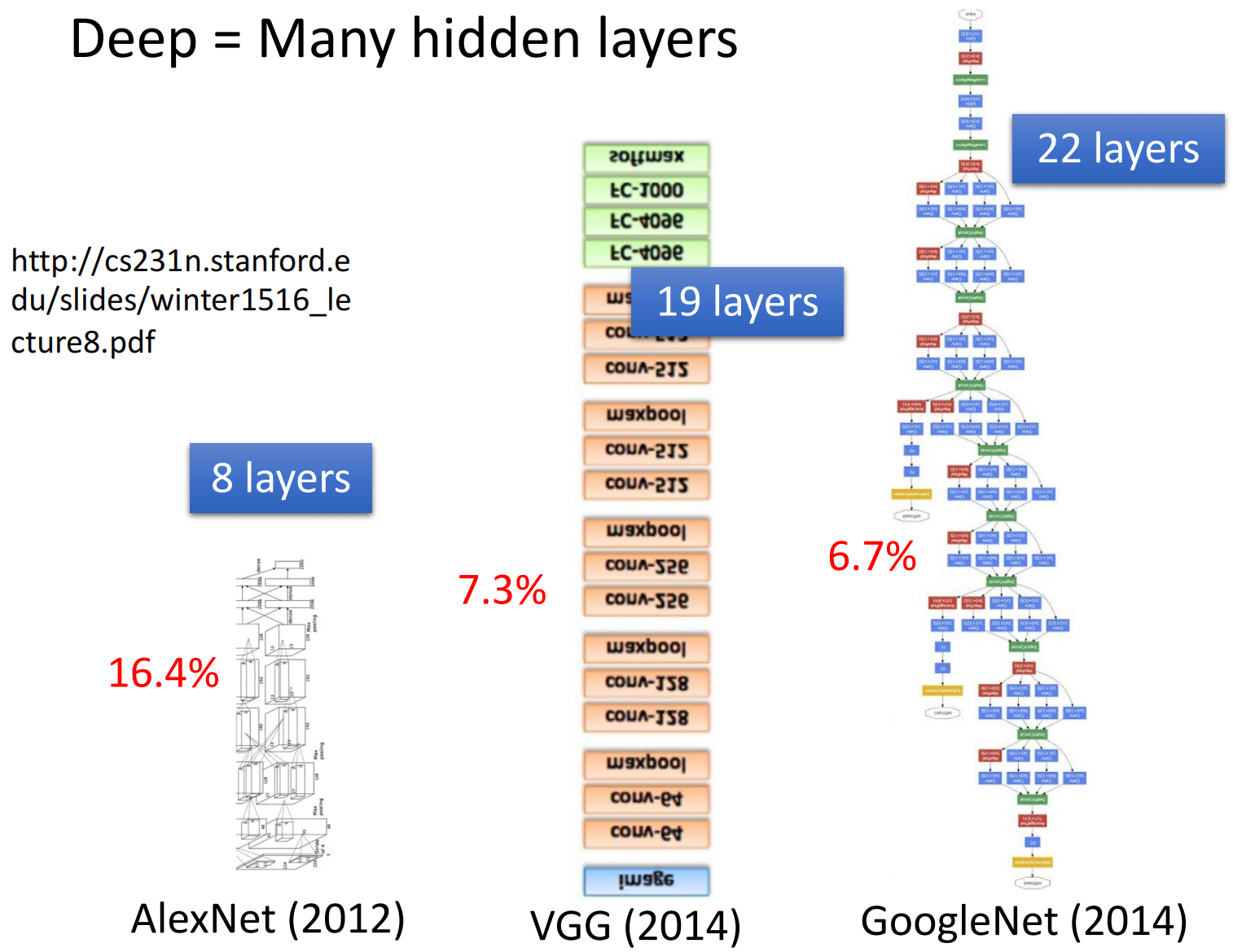
然而他们都不是最深的模型，到了2015年，何凯明的Residual Network有152层，比台湾最高的楼台北101还要高

当然，ResNet能训练的这么深其实是由于他用了特殊的结构，这个结构以后再讲

到这里，我们其实就已经讲完了深度学习

10. Why Deep Nor Fat？

最后，其实有一个微妙的问题，就是我们前面说所有曲线都可以用Piecewise的曲线来逼近，因此对于Neural Network来说，只要有足够多的Neural就可以逼近任意的函数了

那么有一个问题，我们为什么要把网络叠深而不是把所有的神经元放到同一层，即为什么不是把网络变宽而不是变深？

这个留着下节课讲

11. Why don’t we go deeper?

同样是上面的例子，我们可能觉得越深的网络越好，可是事实却是四层的模型不如三层的模型。

这其实是由于出现了Overfitting，即在训练数据上的表现变好而在没看过的数据上的表现变差。

关于Overfitting，我们下次再讲

12. To learn More

最后，是关于这节课一些没有讲到，未来也不一定会用，但是很有用的知识，由于本次课程完全关注深度学习，因此并不会讲解。这是之前的课程的讲解