数学建模算法

发布日期: 2022-01-08

更新日期: 2023-06-01

文章字数: 3.2k

阅读时长: 11 分

阅读次数:

本文主要讲解了数模中帮助进行数据压缩的算法：主成分分析，PCA

主成分分析

数学建模算法10-主成分分析

在前面的一节我们讲解了相关性分析。相关性分析用于判断两个变量之间的相关性。那么就存在一个问题，假设现在我们需要建模的数据有上万行，而每一样的一个example都有二十多个维度。那么要对这样的数据进行分析就会非常占用内存，甚至在数模的这几天里面跑出来这些数据就会占用大部分时间。

因此，为了简化分析、节约时间，在数模中可以使用主成分分析这一方法(Priciple Component Analysis)。

其基本思想就是通过一些手段，实现对数据信息的压缩，从而在损失一部分信息量的前提下实现需要分析的数据的压缩，从而帮助加速分析。

而如何实现损失部分信息带来数据的压缩呢？一个简单的思路其实就可以通过我们前面说的相关性分析，若两个变量$A,B$之间是强相关的（皮尔逊系数大于0.9），那么我们其实可以认为变量$B$的绝大部分信息都蕴含在$A$，我们通过一些方法就可以从A中获得$B$的信息（例如拟合得到的曲线）。那么通过这样，我们其实就没有必要存储$B$的所有的值了，我们只需要存储$A$的值即可。这样做虽然丢失了部分B的信息，但是我们却能够节省内存。

类似的，主成分分析就是同类型的用于进行数据压缩的算法。

数模中常用的数据降维的方法有两种：主成分分析法和因子分析法。两种方法其实差别不大大，而主成分分析得到的指标数量和原来的指标数量，我们选择前几个就行，而因子分析法则是生成我们指定数量的指标数量。

1. 主成分分析的介绍

主成分的概念由Karl Pearson在1901年提出的。他是考察多个变量间相关性一种多元统计方法。

主成分分析研究如何通过少数几个主成分(principal component)来解释多个变量间的内部结构，即从原始变量中导出少数几个主分量，使它们尽可能多地保留原始变量的信息，且彼此间互不相关。

主成分分析的目的：

数据的压缩
数据的解释

其常被用来寻找判断事物或现象的综合指标，并对综合指标所包含的信息进行适当的解释

若直接对原有的指标进行删除，那么存在的一个问题就是一定会丢失掉信息。因此相比于直接简单的删除，需要先对原始数据进行一定的变换，以实现信息的重组，从而保留蕴含更多信息的指标而丢弃蕴含信息较少的指标。

2. 主成分分析的基本思想

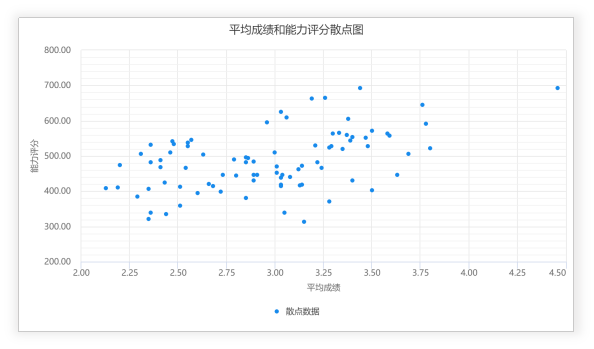
主成分分析的主要思想就是：对这相关变量（为便于理解，先以两个为例）所携带的信息(在统计上信息往往是指数据的变异)进行浓缩处理。假定只有两个变量$x_1$和$x_2$，从散点图可见两个变量存在相关关系，这意味着两个变量提供的信息有重叠。

那么如果把两个变量用一个变量来表示，同时这一个新的变量又尽可能包含原来的两个变量的信息，这就是降维的过程

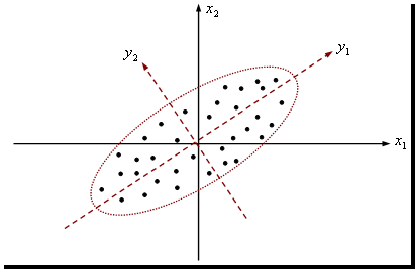
主成分分析的例子

例如，$x_1,x_2$分别表示身高和体重。那么身高和体重确实具有一定的关联，因为身高越高体重一般都会越重。

我们通过坐标轴的旋转，例如旋转到$y_1$和$y_2$，则此时，我们的数据在$y_1$这个轴上的分布越广泛，则其方差相比于原来就会大了很多。而方差在某种意义上可以表达信息的丰富和匮乏程度。方差非常小的一组数据，由于不同的数据间的同质化严重，因此其信息含量非常的匮乏，而方差大的一组数据则由于数据的多样新，因此其中蕴含的信息会更加丰富。

从上面的角度来理解，方差越大的维度其表达能力其实就越强，因为其中蕴含了更多的信息。因此我们其实可以仅仅保存所有数据点的$y_1$的值，那么就可以实现数据的有损压缩。

旋转坐标轴用可以有旋转矩阵来表示，即

$\begin{cases} y_1=a_{11}x_1+a_{12}x_2\\ y_2=a_{21}x_1+a_{22}x_2 \end{cases}$

则我们的关键其实就是找到参数（旋转矩阵）

$A=\begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix}$

那么对于高维数据，其实也是一样的思想，只不过在高维空间中是一个高维椭球，无法直观地观察。

每个变量都有一个坐标轴，所以有几个变量就有几个主轴。首先把椭球的各个主轴都找出来，再用代表大多数数据信息的最长的几个轴作为新变量，这样，降维过程也就完成了。

找出的这些新变量是原来变量的线性组合，叫做主成分。

上面是比较口语化的描述，下面是比较数学一点的描述。

主成分分析就是设法将原来众多具有一定相关性的变量(如$p$个变量)，重新组合成一组新的相互无关的综合变量来代替原来变量。如何处理？

通常数学上的处理就是将原来$p$个变量作线性组合作为新的综合变量。如何选择？

如果将选取的第一个线性组合即第一个综合变量记为$F_1$，自然希望$F_1$尽可能多的反映原来变量的信息。怎样反映?

最经典的方法就是用方差来表达，即$var(F_1)$越大，表示$F_1$包含的信息越多。因此在所有的线性组合中所选取的$F_1$应该是方差最大的，故称之为第一主成分（Principal Component I）。

如果第一主成分不足以代表原来$p$个变量的信息，再考虑选取$F_2$即第二个线性组合。$F_2$称为第二主成分（Principal cComponent II）。 F1和F2的关系？

为了有效地反映原来信息，F1已有的信息就不再出现在F2中，即$cov(F1,F2)＝0$。依此类推，可以获得$p$个主成分。因此，这些主成分之间是互不相关的，而且方差依次递减。在实际中，挑选前几个最大主成分来表征。标准？

各主成分的累积方差贡献率>80%或特征根>1。

3. 主成分分析的数学模型

假定有$n$个样本，每个样本共有$p$个维度，构成一个$n\times p$ 阶的数据阵。

$X= \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1p}\\ x_{21} & x_{22} & \cdots & x_{2p}\\ \vdots & \vdots & \ddots & \vdots\\ x_{n1} & x_{n1} & \cdots & x_{np}\\ \end{bmatrix}$

当p较大时，在p维空间中考察问题比较麻烦。为了克服这一困难，就需要进行降维处理，即用较少的几个综合变量代替原来较多的
变量变量，而且使这些较少的综合变量既能尽量多地反映原来较多变量变量所反映的信息。

要从原来的所有变量得到新的综合变量，一种较为简单的方法是作线性变换，使新的综合变量为原变量的线性组合，即

$\begin{cases} F_1=a_{11}x_1+a_{21}x_2+\cdots+a_{p1}x_p\\ F_2=a_{12}x_1+a_{22}x_2+\cdots+a_{p2}x_p\\ \qquad\qquad\qquad\vdots\\ F_p=a_{1p}x_1+a_{2p}x_2+\cdots+a_{pp}x_p\\ \end{cases}$

此外，由于要求所有的主成分之间是没有信息重叠的，因此需要满足规范化条件，即

$a_{i1}^2+a_{i2}^2+\cdots+a_{ip}^2=1$

此外，主成分分析要求：

原始变量之间存在一定的相关性：如果多个变量相互独立或相关性很小，就不能进行主成分分析。
- 首先可以使用Kaiser-Meyer-Olkin（KMO)检验（检验变量之间的偏相关系数是否过小）来进行判断，要求检验的值大于0.5为可以做，小于0.3为不建议做，0.3~0.5之间是可以做，但是不保证效果
- 其次也可以用Bartlett’s 检验。该检验的原假设是相关矩阵为单位阵（不相关），如果不能拒绝原假设，则不适合进行主成分分析，要求检验的值小于0.05
- 上面两个检验有一个就行
各个综合变量间互不相关，即协方差为0
为了消除变量数量级/分布不同对方差的影响，通常对数据进行标准化处理，变量之间的协方差即为相关系数。

将原有数据案列拆分为

$X= \begin{bmatrix} X_1 & X_2 & \cdots & X_p \end{bmatrix} = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1p}\\ x_{21} & x_{22} & \cdots & x_{2p}\\ \vdots & \vdots & \ddots & \vdots\\ x_{n1} & x_{n1} & \cdots & x_{np}\\ \end{bmatrix}$

则求

$\max_{\vec a} Var(F)， \quad F= \begin{bmatrix} a_1 & a_2 & \cdots & a_p \end{bmatrix} \times \begin{bmatrix} X_1 & X_2 & \cdots & X_p \end{bmatrix}^T$

则将$F$的表达式展开，带入方差的计算式之后即可得到解

4. PCA的Python求解

Python中的scikit-learn中其实已经有了非常成熟的PCA的实现，因此我们直接用即可。

在sklearn中，PCA算法主要是由sklearn.decomposition.PCA类完成。该类的签名如下

class sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None)

其中，我们需要关注的参数有：

n_components：PCA算法中所要保留的主成分个数n，也即保留下来的特征个数n。int 或者 string，缺省时默认为None，所有成分被保留。赋值为int，比如n_components=1，将把原始数据降到一个维度。赋值为string，比如n_components=’mle’，将自动选取特征个数n，使得满足所要求的方差百分比。
copy：bool，True或者False，缺省时默认为True。表示是否在运行算法时，将原始训练数据复制一份。若为True，则运行PCA算法后，原始训练数据的值不会有任何改变，因为是在原始数据的副本上进行运算；若为False，则运行PCA算法后，原始训练数据的值会改，因为是在原始数据上进行降维计算。
whiten：bool，缺省时默认为False。白化，使得每个特征具有相同的方差

其常用的属性如下：

components_ ：返回具有最大方差的成分。
explained_variance_ratio：返回所保留的n个成分各自的方差百分比。
n_components_：返回所保留的成分个数n。

其常用的方法如下：

fit(X,y=None)

fit()可以说是scikit-learn中通用的方法，每个需要训练的算法都会有fit()方法，它其实就是算法中的“训练”这一步骤。因为PCA是无监督学习算法，此处y自然等于None。
fit(X)，表示用数据X来训练PCA模型。

函数返回值：调用fit方法的对象本身。比如pca.fit(X)，表示用X对pca这个对象进行训练。
fit_transform(X)

用X来训练PCA模型，同时返回降维后的数据。newX=pca.fit_transform(X)，newX就是降维后的数据。
inverse_transform()

将降维后的数据转换成原始数据，X=pca.inverse_transform(newX)
transform(X)

将数据X转换成降维后的数据。当模型训练好后，对于新输入的数据，都可以用transform方法来降维。

此外，还有get_covariance()、get_precision()、get_params(deep=True)、score(X, y=None)等方法，以后用到再补充吧。

5. PCA案例

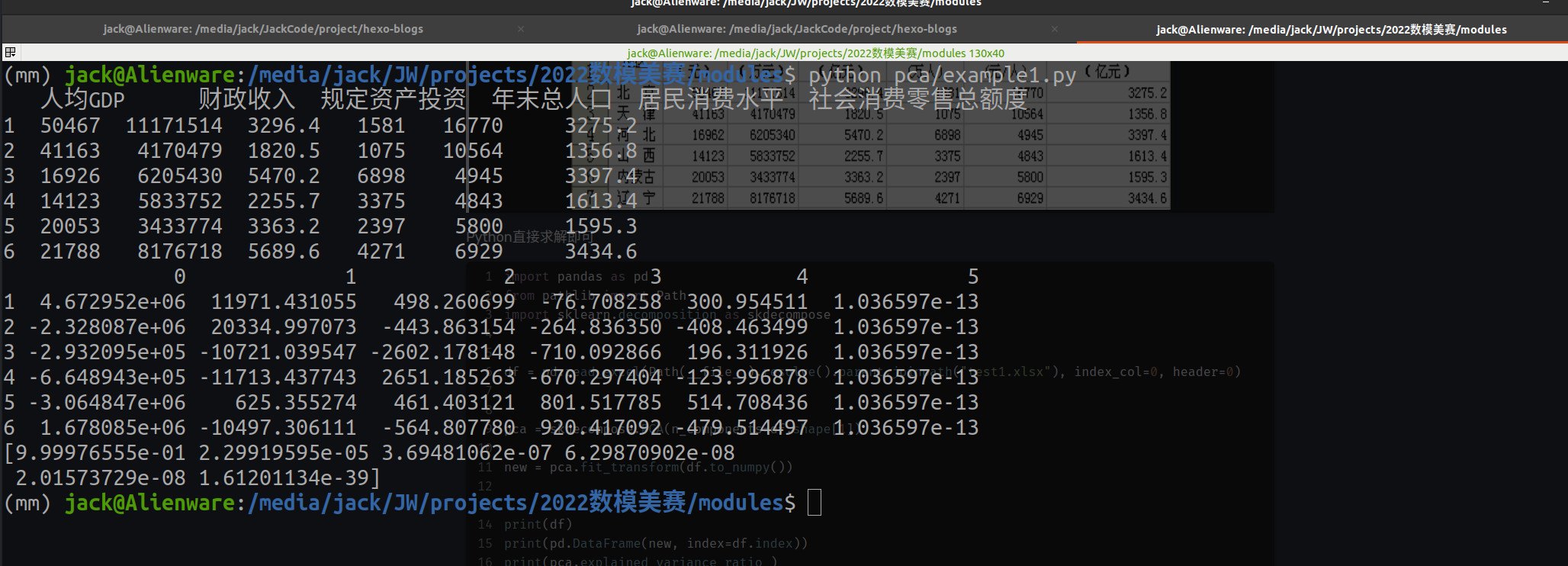
根据我国31个省市自治区2006年的6项主要经济指标数据，进行主成分分析，找出主成分并进行适当的解释

Python直接求解即可

import pandas as pd
from pathlib import Path
import sklearn.decomposition as skdecompose


df = pd.read_excel(Path(__file__).resolve().parent.joinpath("test1.xlsx"), index_col=0, header=0)


pca = skdecompose.PCA(n_components=df.shape[1])

new = pca.fit_transform(df.to_numpy())


print(df)
print(pd.DataFrame(new, index=df.index))
print(pca.explained_variance_ratio_)