本文主要介绍了数学建模中常见的分析与预测算法：灰色关联分析和灰色预测

数学建模算法6-灰色关联分析与预测

灰色关联分析法主要解决对一个系统中多个变量进行分析，从而得出哪些变量和目标变量之间是正相关，哪些是负相关。而灰色预测模型则是在灰色关联分析的基础上，对目标变量未来的发展趋势进行预测的算法。两者都属于灰色系统理论。

因此，灰色系统理论处理的问题为：相关性分析以及预测两类问题

灰色关联分析是数学建模中非常常用的一系列算法，例如：

• CUMCM2003A SARS的传播问题
• CUMCM2005A 长江水质的评价和预测
• CUMCM2006A 出版社的资源配置
• CUMCM2006B 艾滋病疗法的评价及疗效的预测问题
• CUMCM2007A 中国人口增长预测

我们可以更详细的看一下其中的两个问题:

问题一：SARS传播问题

SARS（Severe Acute Respiratory Syndrome，严重急 性呼吸道综合症, 俗称：非典型肺炎）是21世纪第一 个在世界范围内传播的传染病。SARS的爆发和蔓延 给我国的经济发展和人民生活带来了很大影响，我们 从中得到许多重要的经验和教训，认识到定量地研究 传染病的传播规律、为预测和控制传染病蔓延创造条 件的重要性。请你们对SARS 的传播建立数学模型， 具体要求如下：

1. 对附件1所提供的一个早期的模型，评价其合理性和实用性
2. 建立你们自己的模型，说明为什么优于附件1中 的模型；特别要说明怎样才能建立一个真正能够预测 以及能为预防和控制提供可靠、足够的信息的模型， 这样做的困难在哪里？对于卫生部门所采取的措施做 出评论，如：提前或延后5天采取严格的隔离措施， 对疫情传播所造成的影响做出估计。附件2提供的数据供参考。
3. 收集SARS对经济某个方面影响的数据，建立相应的数学模型并进行预测。附件3提供的数据供参考

问题二：长江水质的评价和预测

水是人类赖以生存的资源，保护水资源就是保护我们自己，对 于我国大江大河水资源的保护和治理应是重中之重。专家们呼吁 ：“以人为本，建设文明和谐社会，改善人与自然的环境，减少 污染。” 长江是我国第一、世界第三大河流，长江水质的污染程度日趋 严重，已引起了相关政府部门和专家们的高度重视。2004年10月 ，由全国政协与中国发展研究院联合组成“保护长江万里行”考 察团，从长江上游宜宾到下游上海，对沿线21个重点城市做了实 地考察，揭示了一幅长江污染的真实画面，其污染程度让人触目 惊心。为此，专家们提出“若不及时拯救，长江生态10年内将濒 临崩溃”（附件１），并发出了“拿什么拯救癌变长江”的呼唤 （附件2）。

附件3给出了长江沿线17个观测站（地区）近两年多主要水质指标 的检测数据，以及干流上７个观测站近一年多的基本数据（站点距离 、水流量和水流速）。通常认为一个观测站（地区）的水质污染主要 来自于本地区的排污和上游的污水。 一般说来，江河自身对污染物都有一定的自然净化能力，即污染 物在水环境中通过物理降解、化学降解和生物降解等使水中污染物的 浓度降低。反映江河自然净化能力的指标称为降解系数。 事实上，长江干流的自然净化能力可以认为是近似均匀的，根据 检测可知，主要污染物高锰酸盐指数和氨氮的降解系数通常介于 0 . 1 ~ 0 . 5之间，比如可以考虑取0 . 2　(单位：1 /天)。附件4是 “1995~2004年长江流域水质报告”给出的主要统计数据。下面的附 表是国标(GB3838-2002) 给出的《地表水环境质量标准》中4个主要项 目标准限值，其中Ⅰ、Ⅱ、Ⅲ类为可饮用水

请你们研究下列问题：

1. 对长江近两年多的水质情况做出定量的综合评价，并分析各地区水质的污染状况。
2. 研究、分析长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要在哪些地区?
3. 假如不采取更有效的治理措施，依照过去10年的主要统计数据， 对长江未来水质污染的发展趋势做出预测分析，比如研究未来10年的 情况
4. 根据你的预测分析，如果未来10年内每年都要求长江干流的Ⅳ类 和Ⅴ类水的比例控制在20%以内，且没有劣Ⅴ类水,那么每年需要处理 多少污水？
5. 你对解决长江水质污染问题有什么切实可行的建议和意见

可以看出来，对于SARS问题，第二、三问都涉及了预测，因此可以用灰色模型求解。而对于长江水质，三、四问同样是需要进行预测的。

此外，数学建模中常用的预测方法用：

• 微分方程模型
• 灰色预测模型
• 差分方程模型
• 马尔可夫预测
• 时间序列
• 差值拟合
• 神经网络

不同的预测问题适合不同的预测方法，本文就将讲解其中的灰色关联分析以及灰色预测模型 。

1. 灰色系统理论的介绍

灰色系统理论由华中科技大学控制科学与工程系教授，博士生导师邓聚龙于1982年提出的。它是用来解决信息不完备系统的数学方法，它把控制论的观点和方法延伸到复杂的大系统中，将自动控制与运筹学的数学方法相结合，用独树一帜的方法和手段，研究了广泛存在于客观世界中具有灰色性的问题。在短短的时间里，灰色系统理论有了飞速的发展，它的应用已渗透到自然科学和社会经济等许多领域，显示出这门学科的强大生命力，具有广阔的发展前景。

系统分析的经典方法是将系统的行为看做是随机变化的过程，用概率统计方法，从大量历史数据中寻找统计规律，这对于统计数据量较大情况下的处理较为有效，但对于数据量少的贫信息系统的分析则较为棘手。

灰色系统理论研究的是贫信息建模，它提供了贫信息情况下解决系统问题的新途径。它把一切随机过程看做是在一定范围内变化的、与时间有关的灰色过程，对灰色量不是从寻找统计规律的角度，通过大样本进行研究，而是用数据生成的方法，将杂乱无章的原始数据整理成规律性较强的生成数列后再作研究。灰色理论认为系统的行为现象尽管是朦胧的，数据是杂乱无章的，但它毕竟是有序的，有整体功能的，在杂乱无章的数据后面，必然潜藏着某种规律，灰数的生成是从杂乱无章的原始数据中去开拓、发现、寻找这种内在规律。

1989海洋出版社出版英文版《灰色系统论文集》，同年， 英文版国际刊物《灰色系统》杂志正式创刊。目前，国际、 国内200多种期刊发表灰色系统论文，许多国际会议把灰 色系统列为讨论专题。国际著名检索网站已检索我国学者 的灰色系统论著500多次。灰色系统理论应用范围已拓展 到工业、农业、社会、经济、能源、地质、石油等众多科 学领域，成功地解决了生产、生活和科学研究中的大量实 际问题，取得了显著成果。

灰色系统的应用范畴大致分为以下几方面：

• 灰色关联分析
• 灰色预测（人口预测；灾变预测….等等）
• 灰色决策
• 灰色预测控制

2. 灰色理论的基本概念

1. 白色、黑色和灰色系统

• 白色系统：白色系统是指一个系统的内部特征是完全已知的，即系统的信息是完全充分的。以一个函数为例，我们完全知道这个函数的解析式，因此我们完全知道函数（系统）内部的特征，并且能够给定一个输入，预测其输出。
• 黑色系统：黑色系统是指一个系统的内部信息对外界来说是一无所知的，只能通过它与外界的联系来加以观测研究。同样，以函数为例，黑色系统即我们完全不知道解析式的函数，我们完全不知道这个函数（系统）的内部特征，只能通过大量的数据，利用插值等方法获得近似的函数解析式（利用统计获得系统的信息），然后给定新的输入，给出的预测不一定对。
• 灰色系统：灰色系统内的一部分信息是已知的，另一部分信息是未知的，系统内各因素间有不确定的关系。同样，以函数为例，灰色系统是我们直到部分项的函数，即系统一部分信息是已知的，而另外一部分信息是未知的。

2. 灰色预测法

• 灰色预测法是一种对含有不确定因素的系统，即灰色系统进行预测的方法
• 灰色预测是对既含有已知信息又含有不确定信息的系统进行预则，就是对在一定范围内变化的、与时间有关的灰色过程进行预测的过程

大体上来说，灰色预测通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，并可对原始数据进行生成处 理来寻找系统变动的规律，生成有较强规律性的数 据序列,然后建立相应的微分方程模型，从而预测 事物未来发展趋势的状况

即灰色预测首先判断目标量和哪些量之间是有关系的。例如预测人口增长，那么受限通过灰色关联分析分析得到人口增长是和经济增长有关系、交通发达等等因素有关系。

接下来对原始数据进行生成处理，例如累加或者累减操作生成一个原始数据的序列。而后对该序列建立一个微分方程的模型，最后进行预测

注意，灰色预测法要求对预测对象的值的观测是等时距的。从而利用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的预测对象的特征量，或预测对象达到某一特征量的时间。

3. 灰色预测的四种常见类型

A. 灰色时间序列预测

用观察到的反映预测对象特征的时间序 列来构造灰色预测模型，预测未来某一时刻 的特征量，或达到某一特征量的时间。比如股市分析

B. 畸变预测

通过灰色模型预测异常值出现的时刻， 预测异常值什么时候出现在特定时区内。例如地震预测、异常气候预测、设备异常分析

C. 系统预测

通过对系统行为特征指标建立一组相互 关联的灰色预测模型，预测系统中众多 变量间的相互协调关系的变化。

D. 拓扑预测

将原始数据做曲线，在曲线上按定值寻 找该定值发生的所有时点，并以该定值 为框架构成时点数列，然后建立模型预 测该定值所发生的时点。例如对寻找系统中某个变量等于定值时候的时间点。例如温度控制，温度为27度的时候要升温到30度。那么找到所有温度为27度的时间即拓扑预测。

4. 灰色关联度

大千世界里的客观事物往往现象复杂，因素繁多。我们经常要对系统进行因素分析，这些因素中哪些对系统来讲是主要的，哪些是次要的，哪些需要发展，哪些需要抑制，哪些是潜在的，哪些是明显的？一般来讲，这些都是我们极为关心的问题。事实上，因素间关联性如何、关联程度如何量化等问题是系统分析的关键。

• 例如人口问题。人和社会在一起构成一个系统，影响人口发展变化的因素有社会方面的诸如计划生育、社会治安、社会生活方式等；有经济方面的诸如国民收入、社会福利、社会保险等；还有医疗方面的诸如医疗条件、医疗水平等.……也就是说，人口是多种因素互相关联、互相制约的系统，对这些因素进行分析将有有助于人们对人口的未来预测及人口控制工作。

灰色关联度就是衡量因素间的关联性，对关联性进行量化的指标。

因素分析的基本方法过去主要是采用回归分析（即在大量的数据的基础上，通过回归等手段获得因变量和自变量的解析式的这类方法）等办法，但回归分析的办法有很多欠缺，如要求大量数据、计算量大以及可能出现反常情况等。为克服以上弊病，就产生了灰色关联度分析

灰色关联度是分析向量与向量之间以及矩阵与矩阵之间的关联度。既然计算关联度，一定是计算某一个待比较的数列与参照物（参考数列）之间的相关程度。

3. 灰色关系分析

A. 灰色关联度的计算

灰色关联其实计算的是对比数列和参考数列之间的相似程序/离散程度

1. 选取参考数列

   $$X_0=\{X_0(k)|k=1,2,\cdots,n\}=(X_0(1), X_0(2),\cdots, X_0(n))$$

   上式中，$k$表示时刻

2. 假设存在$m$个比较数列

   $$X_i=\{X_i(k)|k=1,\cdots,n\}=(X_i(1), X_i(2),\cdots, x_i(n)),\qquad i=1,2,\cdots,m$$

   则称

   $$\zeta_i(k)=\frac{\min_{i}\min_k|X_0(k)-x_i(k)|+\rho\max_i\max_k|X_0(k)-X_i(k)|} {|X_0(k)-X_i(k)|+\rho \max_i\max_k|X_0(k)-X_i(k)|}$$

   为比较数列$X_i$对参考数列$X_0$在$k$时刻的关联系数。其中$\rho\in[0,\infin)$为分辨系数，一般而言，$\rho\in[0,1]$。$\rho$越大，分辨率越大；$\rho$越小，分辨率越小，$\rho$一般取0.5。直观的理解即$m$个比较数列全局的最小差距和最大差距的和与当前数列的第$k$项和全局的最大和。描述了当前项的分散度。

3. 关联系数描述了比较数列和参考数列在某一时刻上的关联度，而对于数列整体而言，定义

   $$r_i=\frac 1 n\sum_{k=1}^n\zeta_i(k)$$

   为比较数列$X_i$相对于参考数列$X_0$的关联度。

4. 此外，由于计算关联系数的时候取了绝对值，因此无法通过关联度判断是正相关还是负相关，为此，引入下面的式子进行判断

   $$\begin {aligned} \sigma_i &= \sum_{k=1}^nkX_i(k)-\sum_{k=1}^nX_i(k)\sum_{k=1}^n\frac{k}{n}\\ \sigma_n &= \sum_{k=1}^nk^2-(\sum_{k=1}^nk)2/n \end {aligned}$$

   则有

   $$\begin{cases} sign(\frac{\sigma_i}{\sigma_n})=sign(\frac{\sigma_j}{\sigma_n}), & 则X_i和X_j正相关\\ sign(\frac{\sigma_i}{\sigma_n})=-sign(\frac{\sigma_j}{\sigma_n}), & 则X_i和X_j负相关\\ \end{cases}$$

B. 灰色综合分析的案例

利用灰色关联分析对6位教师工作状况进行综合分析（即判断那个老师能力强，那个老师比较好）：

1. 分析指标包括：专业素质、外语水平、教学工作量、科研成果、 论文、著作与出勤

2. 对原始数据经处理后得到以下数值

   

注意：

1. 在计算灰色关联度的时候，各个指标注意值域要相同
2. 这里由于是通过多个不同的指标来衡量老师，因此当然可以用层次分析法

求解：

1. 计算$|x_0(k)-x_j(k)|$，如下表1

   

2. 求最值：$\min=0，\max=7$

3. 计算相关系数，如下表2

   

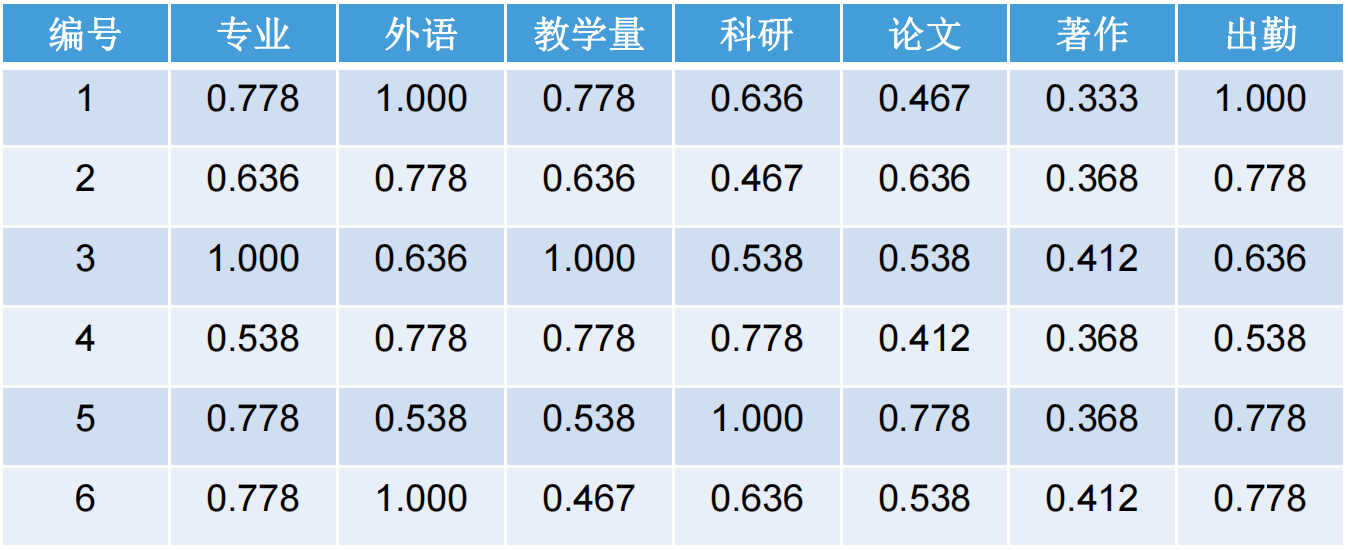
4. 分别计算每个人各指标关联系数的均值（关联序）：如下表3

   

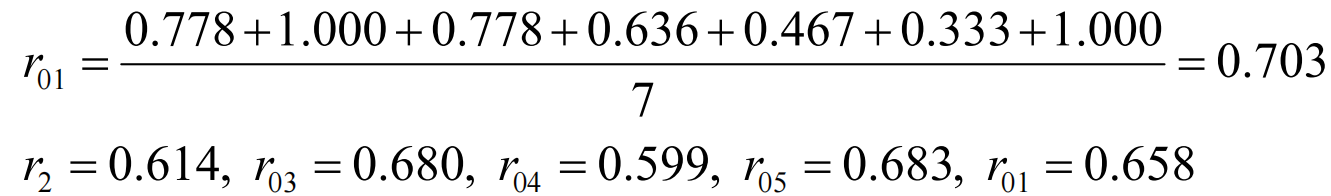
C. 灰色关联度计算代码

Python实现的代码如下：

from typing import *
from pathlib import Path

import numpy as np
from numpy.lib.function_base import iterable
import pandas as pd


class GrayRationalAnalysis(object):
    def __init__(self, df: pd.DataFrame, reference_vector: Union[int, np.ndarray]) -> None:
        super().__init__()
        self.df = df
        self.reference_vector = reference_vector
        self.indices = df.columns

    def run(self, rho=0.5):
        refer_table = self.df.subtract(self.reference_vector, axis=1).abs()
        min_value, max_value = refer_table.min().min(), refer_table.max().max()

        correlation_table: pd.DataFrame = (min_value + rho * max_value) / (refer_table + rho * max_value)
        print(correlation_table.sum(axis=1)/self.df.shape[1])


    @staticmethod
    def build_from_csv(csv_path: Union[str, Path], reference_vector: Union[int, np.ndarray]=9) -> 'GrayRationalAnalysis':
        """
        Notes:
            build_from_csv用于从CSV文件中读取数据并构建灰色分析对象
        """
        csv_path = Path(csv_path) if isinstance(csv_path, str) else csv_path
        df = pd.read_csv(csv_path, header=0, index_col=0)

        if isinstance(reference_vector, int):
            reference_vector: np.ndarray = np.full(df.shape[1], fill_value=reference_vector)
        elif iterable(reference_vector):
            reference_vector = np.array(reference_vector)
            assert df.shape[1] == len(reference_vector), f"维度不匹配"

        return GrayRationalAnalysis(df=df, reference_vector=reference_vector)



if __name__ == "__main__":
    gra = GrayRationalAnalysis.build_from_csv(Path(__file__).resolve().parent.joinpath("./test.csv"), reference_vector=[9,9,9,9,8,9,9]).run()

4. 灰色生成数列

灰色系统理论认为，对于一个系统而言，尽管客观表象复杂，但总是有整体功能的，因此必然蕴含某种内在规律。关键在于如何选择适当的方式去挖掘和利用它。灰色系统是通过对原始数据的整理来寻求其变化规律的， 这是一种就数据寻求数据的现实规律的途径，即为灰色序列的生成。一切灰色序列都能通过某种生成弱化其随机性，显现其规律性。数据生成的常用方式：

• 累加生成
• 累减生成
• 加权累加生成

生成数列的目的在于原始的描述观测的特征量的值的数列具有一定的随机性，而通过多种不同的方式对原始数据进行变换（生成新的数列）的方法就可以减弱其随机性，使得原始数列的特征更加易于发现。

A. 累加生成数列

把数列各项（时刻）数据依次累加的过程称为累加生成过程（AGO）。由累加生成过程所得的数列称为累加生成数列。

设原始数列为

$$x^{(0)}=(x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n)$$

令

$$x^{(1)}(k)=\sum_{i=1}^kx^{(0)}(i), \qquad k=1,2,\cdots,n$$

则称数列

$$x^{(1)}=(x^{(1)}(1), x^{(1)}(2), \cdots, x^{(1)}(n)$$

为数列$x^{(0)}$的一次累加生成数列。类似的，称

$$x^{(r)}=(x^{(r)}(1), x^{(r)}(2), \cdots, x^{(r)}(n),其中 x^{(r)}(k)=\sum_{i=1}^kx^{(r-1)}(i), \quad k=1,2,\cdots,n$$

为$x^{(0)}$的r次累加生成数列

一般经济数列都是非负数列。累加生成能使任 意非负数列、摆动的与非摆动的，转化为非减 的、递增的。例如下图：

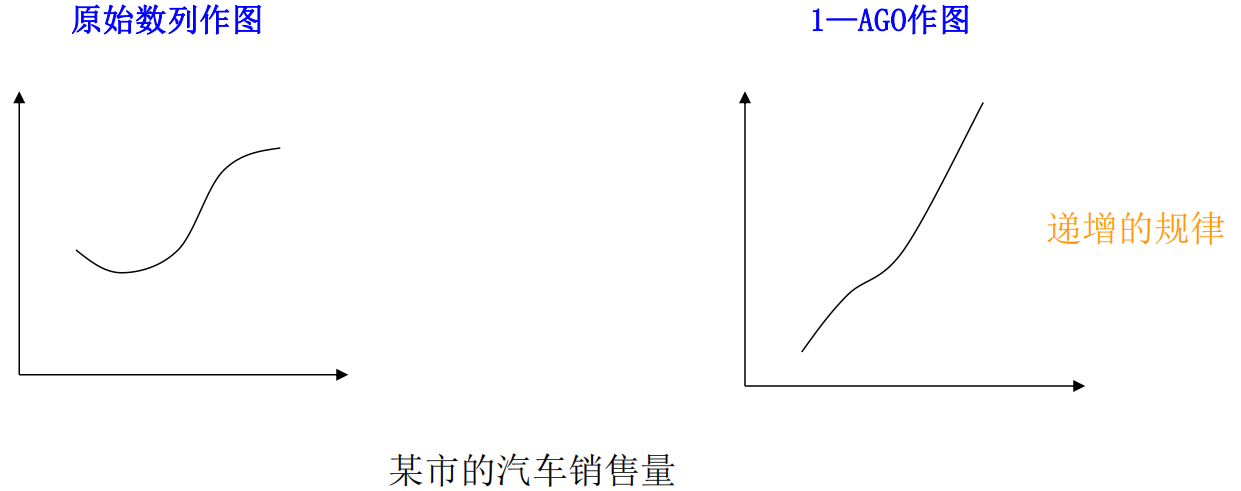
那么原始数列每一项所含的随机影响相对于全体来说就无法造成大的影响，此时找出累加生成数列的规律，而后反推回去得到原始数列的预测就有可能，例如下面的例子。

对于每一年的作物产量进行预测，则由于每年都有病虫害问题导致年产量的曲线难以拟合，而进行一次累加后得到累计年产量曲线则表明在总体上作物产量是以指数关系增长的。对于钢产量也是同理。

B. 累减生成数列

对于原始数据列依次做前后相邻的两个数据相减的运算过程称为累减生成过程（IAGO）

设原始数列为

$$x^{(1)}=(x^{(1)}(1), x^{(1)}(2), \cdots, x^{(1)}(n)$$

令

$$x^{(0)}(k)=x^{(1)}(k)-x^{(1)}(k-1), \qquad k=2,3,\cdots,n$$

则称数列

$$x^{(0)}=(x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n)$$

为数列$x^{(1)}$的一次减生成数列。

其实从符号上可以看出，累加是累减的逆操作。

对于累减生成数列而言，其具有求导的性质，例如下面的例子

C. 加权邻值生成数列

设原始数列为

$$x^{(0)}=(x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n)$$

称$(x^{(0)}(k-1),x^{(0)}(k-1))$为一对邻值，其中称$x^{(0)}(k-1)$为前邻值，称$x^{(0)}(k-1)$为后邻值。

对于任意常数$\alpha\in [0,1]$，取

$$z^{(0)}(k)=\alpha x^{(0)}(k)+(1-\alpha)x^{(0)}(k-1),\qquad k=2,3,\cdots,n$$

则由此得到的数列

$$z^{(0)}=(z^{(0)}(1), z^{(0)}(2), \cdots, z^{(0)}(n)$$

称为数列$x^{(0)}$在权$\alpha$下的邻值生成数列，权$\alpha$称为生成系数

若$\alpha=0.5$，则称数列为均值生成数列，也称为等权邻值生成数列

5. 灰色模型

A. $GM(1,1)$

灰色系统理论是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方程，进而用离散数据列建立微分方程形式的动态模型，即灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数，建立起的微分方程形式的模型，这样便于对其变化过程进行研究和描述。

上面的这段话的关键点：

• 灰色系统理论中定义了定义灰导数和灰微分方程，而灰色模型是基于这些基本概念定义的
• 灰色模型是一个微分方程模型，该微分方程模型是在随机性被削弱的生成数的基础上构建的

设原始数列为

$$x^{(0)}=(x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n)$$

且其一次累加数列为

$$x^{(1)}=(x^{(1)}(1), x^{(1)}(2), \cdots, x^{(1)}(n)$$

则，定义数列$x^{(1)}$的灰导数为

$$d(k)=x^{(0)}(k)=x^{(1)}(k)-x^{(1)}(k-1)$$

设$z^{(1)}(k)$为数列$x^{(1)}$的邻值生成数列，即

$$z^{(1)}(k)=\alpha x^{(1)}(k)+(1-\alpha)x^{(1)}(k-1)$$

则定义$GM(1,1)$的灰微分方程为

$$d(k)+az^{(1)}(k)=b\\或\\x^{(0)}(k)+az^{(1)}(k)=b$$

上式中，$x^{(0)}(k)$是灰导数。而称$a$为发展系数，$z^{(1)}(k)$为白化背景值，b为灰作用量。

将时刻$k=2,3,\cdots,n$带入灰微分方程得

$$\begin{cases} x^{(0)}(2)+az^{(1)}(2)=b\\ x^{(0)}(3)+az^{(1)}(3)=b\\ \cdots\\ x^{(0)}(n)+az^{(1)}(n)=b\\ \end{cases}$$

将上式向量化，则设

$$\vec u = \begin{bmatrix} a\\b \end{bmatrix}$$ $$\vec Y = \begin{bmatrix} x^{(0)}(2)\\ x^{(0)}(3)\\ \vdots\\ x^{(0)}(n) \end{bmatrix}$$ $$B = \begin{bmatrix} -z^{(1)}(2) & 1\\ -z^{(1)}(3) & 1\\ \vdots\\ -z^{(1)}(n) & 1 \end{bmatrix}$$

则$GM(1,1)$可以表示为

$$\vec Y=B\vec u$$

由于$\vec Y$和$B$都可以根据输入获得，因此问题的关键在于求解$\vec u$

微分方程是线性微分方程，因此可以采用一元线性回归，即最小二乘法求估计值

$$\vec u = \begin{bmatrix}a\\b \end{bmatrix}=(B^TB)^{-1}B^TY$$

B. 白化型$GM(1,1)$

$GM(1,1)$是离散的方程，因为其中的导数和微分都是灰导数和灰积分。然而在有的时候，我们如果数列中的每一项之间都是沿着时间收集的，即数列中的每一项都是和时间有关的。那么我们就希望能够用含有时间$t$的微分方程来描述。因此，含有时间$t$的灰色方程即白化型$GM(1,1)$

对于$GM(1,1)$中的灰微分方程

$$x^{(0)}(k)+az^{(1)}(k)=b$$

若将灰导数$x^{(0)}(k)$的每一项$k$（$k=2,3,\cdots,n$）视为连续的变量$t$，即将项的次序视为时间。则$x^{(1)}$是时间$t$的函数，即$x^{(1)}=x^{(1)}(t)$。则$x^{(0)}(k)$就对应导数，即

$$x^{(0)}(k)=x^{(0)}(t)=\frac{dx^{(1)}(t)}{dt}$$

而白化背景就相当于$\alpha x^{(1)}(t)$，故若将$GM(1,1)$视为连续的项，则有

$$\frac{dx^{(1)}(t)}{dt}+\alpha x^{(1)}(t)=b$$

上式两边对$t$同时积分，有：

$$\int_{k-1}^k(\frac{dx^{(1)}(t)}{dt})dt+\int_{k-1}^k ax^{(1)}(t)dt = \int_{k-1}^k bdt$$

左边第一项为$\frac{dx^{(1)}(t)}{dt}$的原函数的第$k$项减第$k-1$的值，即

$$x^{(1)}{(k)}-x^{(1)}(k-1)=x^{(0)}(k)$$

而第二项要求$x^{(1)}(t)$的原函数，则

$$\int_{k-1}^k ax^{(1)}dt\approx az^{(1)}$$

6. $GM(1,1)$的建模步骤

设原始数列为

$$x^{(0)}=(x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n)$$

1. 数据的检验与处理： 为了保证$GM(1,1)$建模方法的可行性，需要对原始数列做必要的检验处理。

   1. 计算原始数列的级比：

      $$\lambda(k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)},\qquad k=2,2,\cdots,n$$

   2. 若所有级比都落在区间

      $$X=(e^{-\frac{2}{n+1}}, e^{\frac{2}{n+1}})$$

      内，则可以直接对原始数列$x^{(0)}$建立$GM(1,1)$模型并进行灰色预测，否则由于不满足灰色模型的理论，因此不能直接用灰色灰色模型

   3. 否则需要对原始数列做适当的变换处理，例如平移（加常数）

2. 建立$GM(1,1)$模型：

   1. 假设通过第一步，得到了满足要求的数列$x^{(0)}$

   2. 则建立白化模型

      $$x^{(0)}(k)+az^{(1)}(k)=b$$

      通过线性回归求得$a$和$b$的值，从而得到模型

      $$x^{(1)}(t)=(x^{(0)}(1)-\frac b a)e^{-a(t-1)}+\frac b a$$

   3. 从而得到预测值

      $$x^{(1)}(k+1)=(x^{(0)}(1)-\frac b a)e^{-ak}+\frac b a,\qquad k=1,2,\cdots,n-1$$

   4. 最终得到预测值

      $$x^{(0)}(k+1)=x^{(1)}(k+1)-x^{(1)}(k),\qquad k=1,2,\cdots,n-1$$

3. 检验预测值：为了检测$GM(1,1)$的预测是否正确，还需要对预测进行检测

   1. 残差检验：计算相对残差，即原值减去预测值比上原值

      $$\varepsilon(k)=\frac{x^{(0)}(k)-\hat {x}^{(0)}(k)}{x^{(0)}(k)},\qquad k=1,2,\cdots,n$$

      若对于所有的$|\varepsilon(k)|<0.1$，则可以认为模型的预测达到较高的精度；否则，若对于所有的$|\varepsilon(k)|<0.2$，则认为模型的预测达到一般精度

   2. 级比检验：计算

      $$\rho(k)=1-\frac{1-0.5a}{1+0.5a}\lambda(k)$$

      若对于所有的$|\rho(k)|<0.1$，则认为模型的预测达到了较高的精度；否则，若对于所有的$|\rho(k)|<0.2$，则认为模型达到了一般的要求

7. 灰色预测Python求解

基于Numpy和Pandas实现的灰色预测模型代码如下

A. 代码

from pathlib import Path
import re
from typing import Union

import numpy as np
import pandas as pd
import scipy.stats as scist



class GrayForcast(object):
    def __init__(self, series: Union[pd.DataFrame, pd.Series]) -> None:
        super().__init__()
        self.index: pd.Index = series.index
        self.x0 = series.to_numpy()

    def train(self, verbose: bool = True):
        # 计算级比
        right_moved: np.ndarray = np.array([0, *(self.x0[:-1])])
        self.lambdas: np.ndarray = right_moved / self.x0

        # 级比检验
        n = len(self.x0)
        assert (l:=(np.exp(-2/n) < self.lambdas[1:]) & (self.lambdas[1:] < np.exp(2/n))).all(), f"级比检验未通过:{l}, 其中第{list(np.where(l==False)[0])}位:{self.x0[1:][~l]} 出错，数据不适合直接进行灰色预测"
        if verbose:
            print("级比检验通过")

        # GM(1,1)建模
        # 一次累加
        self.x1 = np.cumsum(self.x0)

        # 构建B和Y矩阵
        Y = self.x0[1:].reshape(-1, 1)
        right_moved = np.array([*(self.x1[:-1])])
        left_moved = np.array([*(self.x1[1:])])
        B = np.vstack(tup=(-1 * (left_moved + right_moved) / 2, np.ones_like(right_moved))).T

        # 线性回归
        self.u = np.linalg.inv(B.T @ B) @ B.T @ Y

        # 模型检验
        x0_pred = self.predict(items=7)

        # 残差检验
        relative_residual = np.abs((self.x0 - x0_pred) / self.x0)
        if (l:= (relative_residual < 0.1)).all():
            print("残差检验通过，所有残差小于0.1，达到高精度")
        else:
            if (l:= (relative_residual < 0.2)).all():
                print("残差检验通过，所有残差小于0.2，达到一般精度要求")
            else:
                assert False, f"残差检验未通过，第{np.where(l==False)[0]}位:{relative_residual[~l]}大于0.2"

        # 级比检验
        rho = 1- (1 - self.u[0, 0] * 0.5) / (1 + self.u[0, 0] * 0.5) * self.lambdas
        if (l:= (rho[1:] < 0.1)).all():
            print("级比检验通过，所有级比小于0.1，达到高精度")
        else:
            if (l:= (rho[1:] < 0.2)).all():
                print("级比检验通过，所有级比小于0.2，达到一般精度要求")
            else:
                assert False, f"级比检验未通过，第{np.where(l==False)[0]}位:{rho[1:][~l]}大于0.2"
        rho[0] = np.nan

        if verbose:
            df = np.vstack(tup=(self.x0, x0_pred, self.x0-x0_pred, relative_residual*100, rho))
            df = pd.DataFrame(df.T, index=self.index, columns=["原始值","预测值","残差","相对残差(%)","级比偏差"])
            print(df)



    def predict(self, items: int) -> np.ndarray:
        a, b = self.u[0, 0], self.u[1,0]
        def x1_kp1(k: int):
            if k == 0:
                return self.x0[0]
            else:
                return (self.x0[0] - b/a) * np.exp(-a * k) + b/a
        x1_pred = np.array([x1_kp1(i) for i in range(items)])
        right_moved = np.array([0, *(x1_pred[:-1])])
        x0_pred = x1_pred - right_moved
        return x0_pred


    @staticmethod
    def preprocess_donothing(gf: "GrayForcast") -> "GrayForcast":
        return gf

    @staticmethod
    def build_from_csv(csv_path: Union[str, Path], target_col: Union[None, int, str]=None) -> "GrayForcast":
        csv_path = csv_path if isinstance(csv_path, Path) else Path(__file__).resolve().parent.joinpath(csv_path)
        df : pd.DataFrame = pd.read_csv(csv_path, header=0, index_col=0)

        assert (multiple:=df.shape[1] != 1) and target_col is not None, f"CSV文件存在多个序列：{df.columns}，请指定target_col参数指定需要预测的序列"

        if multiple:
            if isinstance(target_col, str):
                target_col = df.T.loc[target_col]
            elif isinstance(target_col, int):
                target_col = df.iloc[:, target_col]
        else:
            target_col = df
        return GrayForcast(series=target_col)

    @staticmethod
    def build_from_excel(csv_path: Union[str, Path], target_col: Union[None, int, str]=None) -> "GrayForcast":
        csv_path = csv_path if isinstance(csv_path, Path) else Path(__file__).resolve().parent.joinpath(csv_path)
        df : pd.DataFrame = pd.read_excel(csv_path, header=0, index_col=0)

        assert (multiple:=df.shape[1] != 1) and target_col is None, f"xlsx文件存在多个序列：{df.columns}，请指定target_col参数指定需要预测的序列"

        if multiple:
            if isinstance(target_col, str):
                target_col = df.loc[target_col]
            elif isinstance(target_col, int):
                target_col = df.iloc[:, target_col]
        else:
            target_col = df
        return GrayForcast(series=target_col)


if __name__ == "__main__":
    gf = GrayForcast.build_from_csv(csv_path="./test2.csv", target_col="噪声")
    gf.train()
    print(gf.predict(10))

B. 使用说明

代码从指定的表格中读取数据，然后先训练得到参数，最后通过预测指定，需要预测的项数即可

表格要求如下：第一列为序号，其余列为对比数列，对比数列沿列展开，若表格有多列则需要指定计算的列的名称

使用结果如下

8. 灰色预测案例

灰色预测模型处理的问题基本都是预测模型

A. 投资理财问题

银行有各种投资理财产品，客户可根据自己的资金实力和 投资偏好来自由选择，并且一般会有“10天犹豫期”，在 这10天里如果对自己购得的理财产品不放心或者不满意通 常情况下是可以退买的，这时候是不收手续费的。否则逾 期退买将收取一定的手续费。 通过对客户退买行为数据的分析，发现客户购得理财产品 后的每一天继续持有的客户比例依次是[92.810 97.660 98.800 99.281 99.537 99.537 99.817 0.00](单位%)，从这组数列可以看出退买高发期是在前几天，后续退买的可能性持续衰减。建立$GM(1,1)$模型对以上数据进行分析。

B. 道路噪声平均值

北方某城市1986～1992 年道路交通噪声平均声级数据见表6，单位为db(A)

利用上面的代码，准备好表格数据，然后开始预测

C. 公司利润预测

已知某公司1999-2008年的利润为(单位：元/年)： [89677,99215,109655,120333,135823,159878,182321,209407, 246619,300670],现在要预测该公司未来几年的利润情况。

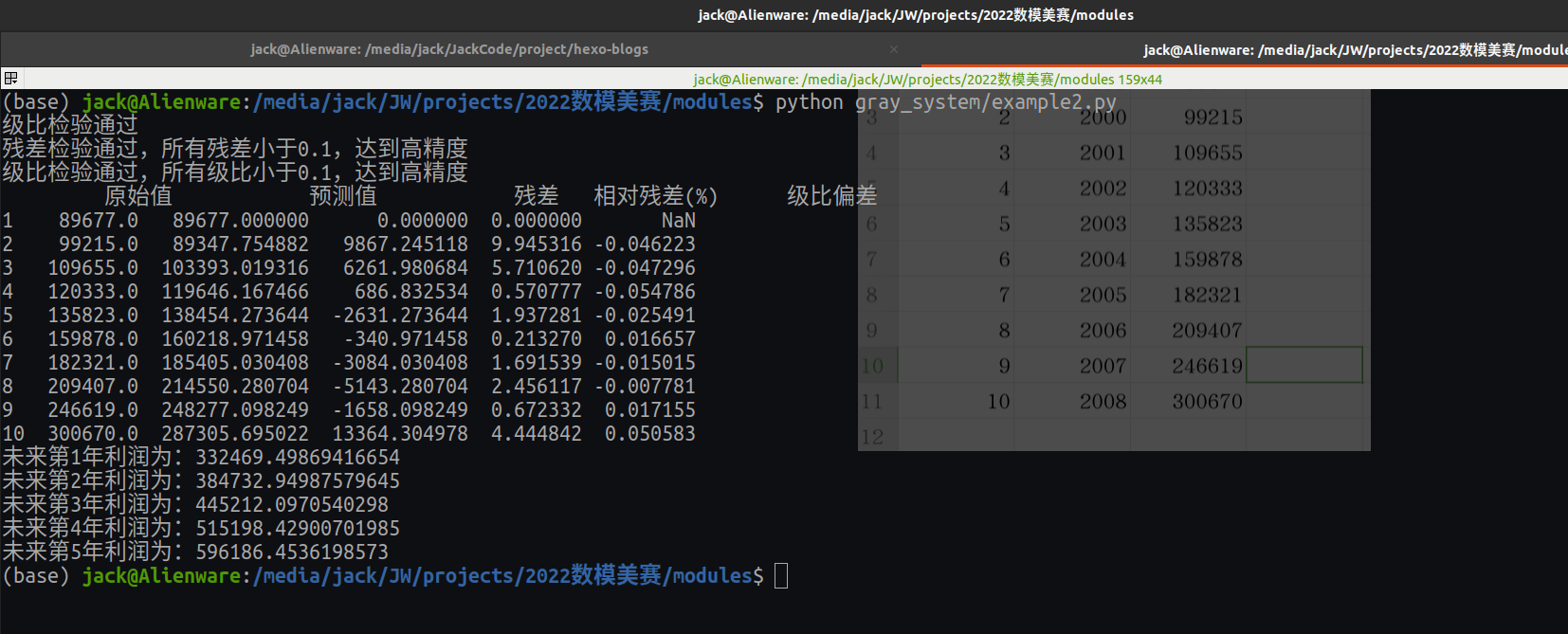
把上面的数据制作成下面的表格

得到未来五年利润的预测如下

D. SARS病毒影响

2003年的SARS疫情对中国部分行业的经济发展产生了一 定的影响，特别是对帮分疫情较严重的省市的相关行业所造成的影响是明显的，经济影响主要分为直接经济影响和 间接影响。直接经济影响涉及到商品零售业、旅游业、综合服务等行业。很多方面难以进行定量地评估，现仅就 SARS疫情较重的某市商品零售业、旅游业和综合服务业的影响进行定量的评估分析。

究竟SARS疫情对商品零售业、旅游业和综合服务业的影 响有多大，已知该市从1997年1月到2003年10月的商品零 售额、接待旅游人数和综合服务收入的统计数据如下表1 、表2、表3．

试根据这些历史数据建立预测评估模型，评估2003年SARS疫 情给该市的商品零售业、旅游业和综合服务业所造成的影响。

对SARS病毒影响的评估，那么可以用没有疫情和有疫情的对比实现。例如要探究SARS对零售业的影响，那么其实可以首先预测出来没有SARS零售业本来的指标，然后和有SARS的指标进行对比，从而给出对SARS病毒的影响。

因此思路如下：

根据所掌握的历史统计数据可以看出，在正常情况下，全 年的平均值较好地反映了相关指标的变化规律，这样可以 把预测评估分成两部分：

1. 利用灰色理论建立灰微分方程模型，由1997~2002年的 平均值预测2003年平均值
2. 通过历史数据计算每个月的指标值与全年总值的关系 ，从而可预测出正常情况下2003年每个月的指标值，再与 实际值比较可以估算出SARS疫情实际造成的影响

具体求解略