本文主要讲解了数学建模中常见的一类问题:非线性规划,及其求解

数学建模算法4-非线性规划
在前面的几篇文章中,我们介绍了线性规划、整数规划以及01规划,并且给出了如何利用Python来对他们进行求解。
但是在显示问题中,的确有很多规划问题他们的约束都不是线性的,或者他们的目标函数也不是线性的。可是我们在数学建模的过程中,我们自己提出来的模型很有可能是非线性的规划问题,此时就我们就不得不对非线性的规划问题进行求解。
为此,本文介绍了什么是非线性规划问题,以及如何利用Python求解非线性规划问题。
1. 非线性规划问题介绍
如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问题(Nonlinear Programming,NP)。一般说来,解非线性规划要比解线性规划问题困难得多。而且,也不像线性规划有单纯形法这一通用方法,非线性规划目前还没有适于各种问题的一般算法,各个方法都有自己特定的适用范围。例如:
- 20世纪50年代,H.W.Kuhn 和 A.W.Tucker 提出了非线性规划的基本定理,为非线性规划奠定了理论基础
- 50、60 年代出现了许多解非线性规划问题的有效算法
- 80年代后,随着计算机技术的快速发展,非线性规划方法取得了长足进步,在信赖域法、稀疏拟牛顿法、并行计算、内点法和有限存储法等领域取得了丰硕的成果。
不过就和前面的文章一样,我们其实并不需要关注这些算法的原理以及如何如何实现这个算法,我们只需要会用就行了,因此下面就围绕非线性规划问题进行求解。
2. 非线性规划的标准形式
类似于线性规划的标准形式,非线性规划的约束条件可以划归称两类:第一类是$\leq型,第二类是$$=$型。
我们下面给出来非线性规划的标准形式:
对后面两个式子进行缩写,得到
3. 非线性规划问题的Python求解
使用Python求解非线性规划问题,主要使用SciPy中的minimize函数,这个函数实际上是多个优化算法的接口。
该函数的函数头如下
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
其中,我们需要关注的变量只有下面几个:
fun:以Python中的函数的形式定义的目标函数
x0:在有些求解非线性约束的方法中(例如拟牛顿法)需要梯度来帮助求解,因此需要一个初始值进行迭代
bounds:每个变量的上下限
constrains:元组形式的约束条件,其中每个约束条件是元组中的一个项,用一个字典表示
以字典形式表示的约束条件按照如下方式
{'type': 'ineq', 'fun': functionname}其中:
- type是约束的类型,是等式约束还是不等式约束,等式约束为eq,不等式约束为ineq,默认不等式约束为大于等于0
- fun是以Python的函数的形式定义的约束的函数
此外,需要注意的是,约束的函数和目标变量的函数都是需要接受一个变量作为输入,这个变量即决策变量组成的向量,而决策向量的形状由x0决定
例如对下面的非线性规划问题进行求解
A. 定义决策变量
定义决策变量很简单,直接写一个函数就行了,注意这个函数的输入是和x0形状相同的Numpy的array
import numpy as np
import scipy.optimize as scopt
def objective(x: np.ndarray):
return sum(x ** 2)
B. 定义约束
注意,约束的定义也是写成Python中的函数,函数的参数也是Numpy的array
def constrain1(x: np.ndarray):
return x[0] ** 2 - x[1] + x[2] ** 2
def constrain2(x):
return -(x[0] + x[1] ** 2 + x[2] ** 3 - 20)
def constrain3(x):
return -x[0] - x[1] ** 2 + 2
def constrain4(x):
return x[1] + 2 * x[2] ** 2 - 3
def x0_bound(x):
return x[0] - 0
def x1_bound(x):
return x[1] - 0
def x2_bound(x):
return x[2] - 0
constrains = (
{"type": "ineq", "fun": constrain1},
{"type": "ineq", "fun": constrain2},
{"type": "eq", "fun": constrain3},
{"type": "eq", "fun": constrain4},
{"type": "ineq", "fun": x0_bound},
{"type": "ineq", "fun": x1_bound},
{"type": "ineq", "fun": x2_bound},
)
C. 调用求解
调用函数求解,依次填入参数即可
x0 = np.array([1, 2, 3])
result: scopt.OptimizeResult = scopt.minimize(fun=objective, x0=x0, constraints=constrains)
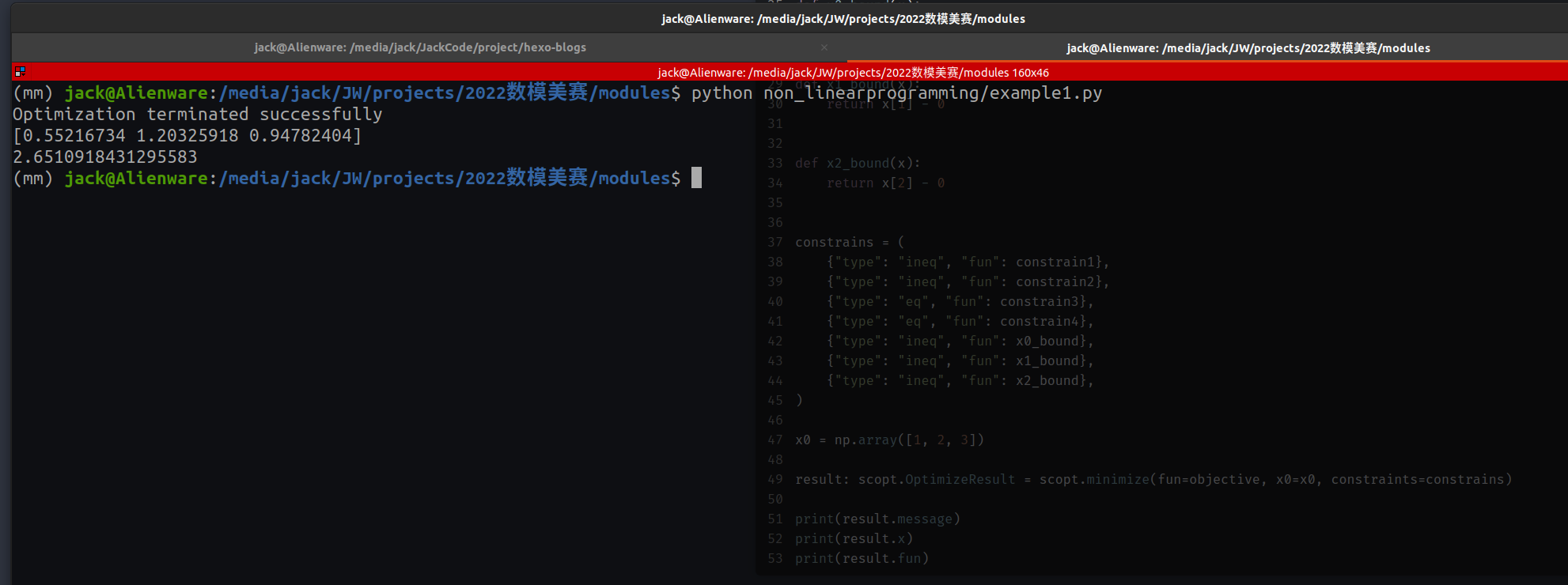
print(result.message)
print(result.x)
print(result.fun)
求解结果
D. 完整代码
完整的代码如下,注意约束条件也可以指定bounds参数
import numpy as np
import scipy.optimize as scopt
def objective(x: np.ndarray):
return sum(x ** 2)
def constrain1(x: np.ndarray):
return x[0] ** 2 - x[1] + x[2] ** 2
def constrain2(x):
return -(x[0] + x[1] ** 2 + x[2] ** 3 - 20)
def constrain3(x):
return -x[0] - x[1] ** 2 + 2
def constrain4(x):
return x[1] + 2 * x[2] ** 2 - 3
def x0_bound(x):
return x[0] - 0
def x1_bound(x):
return x[1] - 0
def x2_bound(x):
return x[2] - 0
constrains = (
{"type": "ineq", "fun": constrain1},
{"type": "ineq", "fun": constrain2},
{"type": "eq", "fun": constrain3},
{"type": "eq", "fun": constrain4},
# {"type": "ineq", "fun": x0_bound},
# {"type": "ineq", "fun": x1_bound},
# {"type": "ineq", "fun": x2_bound},
)
bounds = [(0, None) for i in range(3)]
x0 = np.array([1, 2, 3])
result: scopt.OptimizeResult = scopt.minimize(fun=objective, x0=x0, constraints=constrains, bounds=bounds)
print(result.message)
print(result.x)
print(result.fun)
4. 非线性规划例子
下面介绍即非线性规划的数学模型的例子
A. 选址供应问题
问题的具体描述如下

1) 问题分析
第一问中需要进行决策的变量就是从某个料场到某个工地需要运输多少的水泥,例如从料场A运输到工地1。因此考虑到有两个料场,每个料场都可以去六个工地,因此决策变量实际上用12个。
而第二问则需要决策的变量变成了两个新料场的位置,因此需要决策变量就成了两个新料场的坐标,因此第二问的决策变量有4个。
因此两问分别对应两个规划问题。
2) 建立模型
第一问
记工地的位置为$(ai,b_i)$,水泥日用量为$d_i,i=1,\cdots,6$;料场的位置记为$(x_j, y_j),j=1,2$。则设料场$j$向工地$i$的运输量为$X{ij}$
则针对第一问,建立的数学模型如下
- 第二问
3) 问题求解
略



