数学建模算法3-01规划

Python Math Modeling Linear Programming 01规划
数学建模算法
发布日期:   2022-01-03
更新日期:   2023-06-01
文章字数:   3.5k
阅读时长:   13 分
阅读次数:  

本文主要讲解了数学建模中常见的一类问题：01规划，及其求解

01规划问题

数学建模算法3-01规划

前面我们介绍了数学规划中的线性规划、整数规划。其实对于整数规划来说，还有一类特殊的规划问题就是决策变量的取值只能为0或者1，这样的问题我们称为0-1规划。

01规划问题通常出现在指派问题中，例如一共有很多种任务，多个不同的人完成每种任务需要的时间不同，求最短耗时。那么这里是否派A去做任务X就是一个只能取0或者1的变量。因此这样的问题就可以用01规划来解决。更多可以用01规划求解的问题在后面会进行介绍。

1. 01规划问题介绍

其实对于01规划问题来说，如果假设所有的变量的取值都是0或者1，并且所有变量之间都是独立的，那么我们其实用整数规划就能求解。因为所有变量独立的01规划问题相比于整数规划问题，只是单纯的限制了每个决策变量的定义域为$0\leq x_i\leq 1$。

所以对于所有变量独立的01规划来说，给所有的01变量添加大于等于0且小于等于1的约束即可。

然而01规划中，真正难处理的是01变量之间会相互影响的01规划。例如上面的投资问题，设$x_i$表示是否投资第$i$个项目，那么$x_i$的取值只能在0和1之间。

但是项目I、II、III之间会相互影响，即是否投资项目II会影响到项目I、项目III的投资，而项目I是否投资又会影响到项目V是否投资。

因此，称处01变量之间相互制约的条件为互斥条件，而为了处理含互斥条件的的01问题，在原有的约束的基础上引入互斥约束

01规划问题

再举一个例子（如下图），新工序和原工序都是线性约束，但是在考虑两种工序到底用哪一个才能使得收益最大的时候，就可以另设一个01变量$y$表示是否用原工序。此时问题就成了混合线性规划问题。

当然这里也可以设$x_0$表示是否用原工序，$x_1$表示是否用新工序，那么再额外引入一个互斥约束为$x_1+x_1=1$。

注意，之所以要$M$是一个充分大的数（无穷），是因为$3x_1+5x_2\leq\infin$这个约束条件等价于没有，因为$x_1$和$x_2$都可以取任意的值

互斥约束问题

2. 01规划问题的数学化

要对01规划进行进行求解，就需要首先写出来01规划的标准式，然后针对标准式运用算法进行求解

A. $\leq$类型

设从下面$p$个约束条件中选择$q$个约束条件

设

则需要添加的互斥约束为：

上面这两个约束也非常好理解：

  • 不选的约束的和加起来等于$p-q$
  • 不选这个约束则表示让该改约失效，即加上一个充分大的数即可

3. 01规划问题举例

A. 固定费用问题

服装公司租用生产线拟生产T恤、衬衫和裤子。 每年可用劳动力8200h，布料8800m2。生产每类商品需要的劳动力、布料以及售价等信息如下表所示。求该怎样生产产品可以获得最大收益。

商品信息表

上述问题中的变量其实有两类，第一类是某个商品该生产多少件，第二类是是否租用该商品的生产线。很明显，第二类变量是01变量。

设$y_i$表示是否要租用第$i$类生产线，$x_j$表示第$j$类商品生产多少件，那么上述问题的数学模型如下：

B. 指派问题

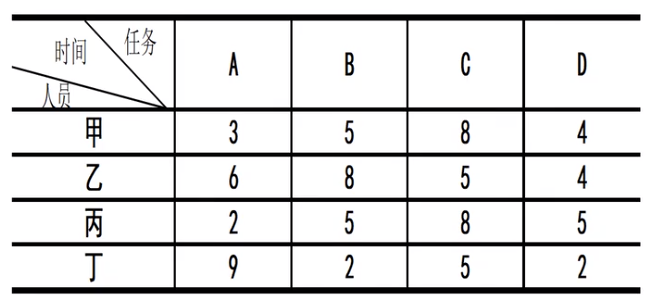
甲乙丙丁四个人，ABCD四项工作，每个人完成每项工作用时如下表。要求每人只能做一项工 作，每项工作只由一人完成，问如何指派总时间最短？

工作用时表

上述问题中，一个人完成四个工作有4个时间，那么4个人就一种16个时间。针对这16个时间，引入变量$x_{ij}$

则指派问题的数学模型如下

上述八个约束中，前四个约束为一个人只能做一项工作，而后四个约束为一个工作只能由一个人完成。

C. 指派问题的标准形式

$n$个人和$n$个工作，已知第$i$个人完成第$j$个工作的代价$c_{ij}$，要求每项工作只能由一个人完成，每个人只能完成其中的一项工作，问如何分配工作可以使总代价最少？

称矩阵$C$为指派问题的系数矩阵

设$x_{ij}$表示第$i$个人做第$j$项工作的状态，即

则称

为指派问题的解矩阵。由于指派问题的要求，解矩阵每行每列都仅有一个1，类似于八皇后问题的退化版。

而指派问题的数学模型为

D. 非标准形式的指派问题

1) 最大化指派问题

指派问题中是要求画的总时间最少，然而在一些指派问题的变体中，要求优化目标最大，则此时取系数矩阵中最大的元素$c’=\max C$，令

然后转化为了指派问题，对其你找指派问题进行求解即可

2) 人数和工作数不相等

在指派问题中，有$n$个人做$n$项工作，然而在一些变体问题中却会存在两者数量不相等的情况，为此

  • 人少工作多：添加虚拟的人，使得人数和工作数相等，注意，添加的虚拟人的代价都是0
  • 人多工作少：添加虚拟的工作，使得人数和工作数相等，注意，添加的虚拟工作的代价都是0

4) 多面手问题

标准的指派问题中要求一个人只能做一项工作，然而若一个人可以做三四项工作，那么把这个人变为几个相同的人即可

5) 禁止某人做某工作

为此，将该人做某工作的代价记为无穷大即可

4. 匈牙利算法解01规划问题

下面将结合指派问题讲解如何用匈牙利算法求解01规划问题

匈牙利算法步骤如下：

  1. 对指派问题的系数矩阵$(c{ij})$进行变换，使其变为$(b{ij})$，$(b_{ij})$满足在每行每列中都有0元素。变换步骤如下

    • 对$(c_{ij})$每行元素减去该行最小元素
    • 从得到的新的矩阵每列元素减去该列的最小元素

  2. 进行试指派，以寻求最优解

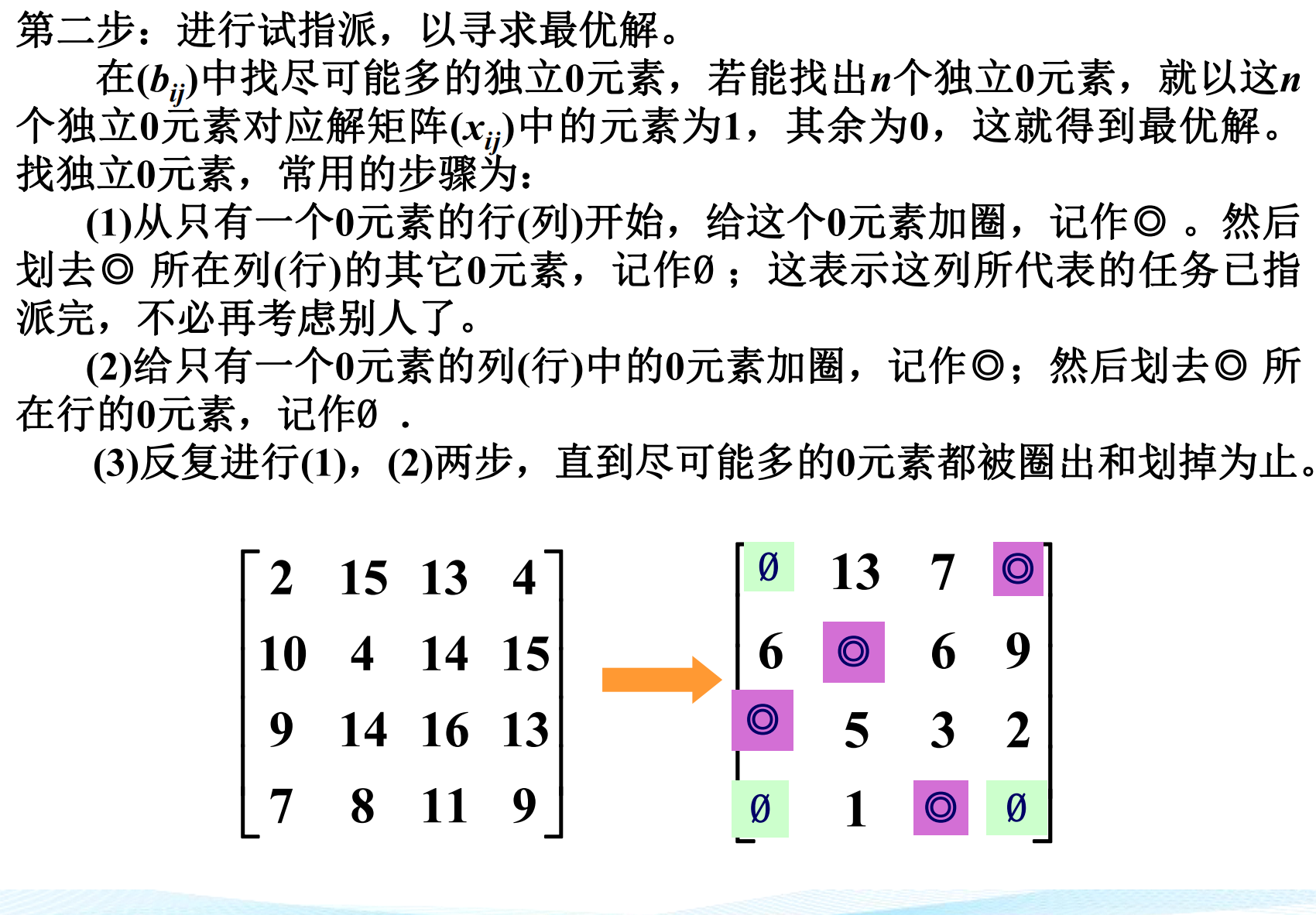
    在$(b{ij})$中找尽可能多的独立0元素，若能找出$n$个独立0元素（独立0元素指该元素所在的行和列数不相等），就以这$n$个独立0元素对应解矩阵$(x{ij})$中的元素为1，其余为0，这就得到最优解。找独立0元素，常用的步骤为：

    1. 从只有一个0元素的行(列)开始，给这个0元素加圈，记作◎ 。然后划去◎ 所在列(行)的其它0元素，记作Ø；这表示这列所代表的任务已指派 完，不必再考虑别人了。
    2. 给只有一个0元素的列(行)中的0元素加圈，记作◎；然后划去◎ 所 在行的0元素，记作Ø ．
    3. 反复进行(1)，(2)两步，直到尽可能多的0元素都被圈出和划掉为止
    4. 若仍有没有划圈的0元素，且同行(列)的0元素至少有两个， 则从剩有0元素最少的行(列)开始，比较这行各0元素所在列中0元 素的数目，选择0元素少的那列的这个0元素加圈(表示选择性多的 要“礼让”选择性少的)。然后划掉同行同列的其它0元素。可反 复进行，直到所有0元素都已圈出和划掉为止
    5. 若◎ 元素的数目m 等于矩阵的阶数n，那么这指派问题的 最优解已得到。若m < n, 则转入下一步

  3. 作最少的直线覆盖所有0元素

    1. 对没有◎的行打√号
    2. 对已打√号的行中所有含Ø元素的列打√号
    3. 再对打有√号的列中含◎ 元素的行打√号
    4. 重复(2)，(3)直到得不出新的打√号的行、列为止
    5. 对没有打√号的行画横线，有打√号的列画纵线，这就得到覆盖 所有0元素的最少直线数 l 。l 应等于m，若不相等，说明试指派过 程有误，回到第二步(4)，另行试指派；若 l＝m < n，须再变换当前 的系数矩阵，以找到n个独立的0元素，为此转第四步

  4. 变换矩阵(bij)以增加0元素

    1. 在没有被直线覆盖的所有元素中找出最小元素，然后打√各行都减去 这最小元素；打√各列都加上这最小元素（以保证系数矩阵中不出现 负元素）。新系数矩阵的最优解和原问题仍相同。转回第二步

实际上，单纯的看自然语言的描述不好懂，因此下面根据不同的例子来进行讲解匈牙利算法。

A. 例子一

求解下面的指派问题

例子一

  1. 第一步：对系数矩阵进行变换

第一步：变换系数矩阵

  1. 第二步：试指派，寻找最优解，寻找独立的0元素

    1. 寻找独立0元素
      第二步：试指派

    2. 判断是否完成求解

      第二步:判断是否完成求解

B. 例子二

求解下面的指派问题

例子二

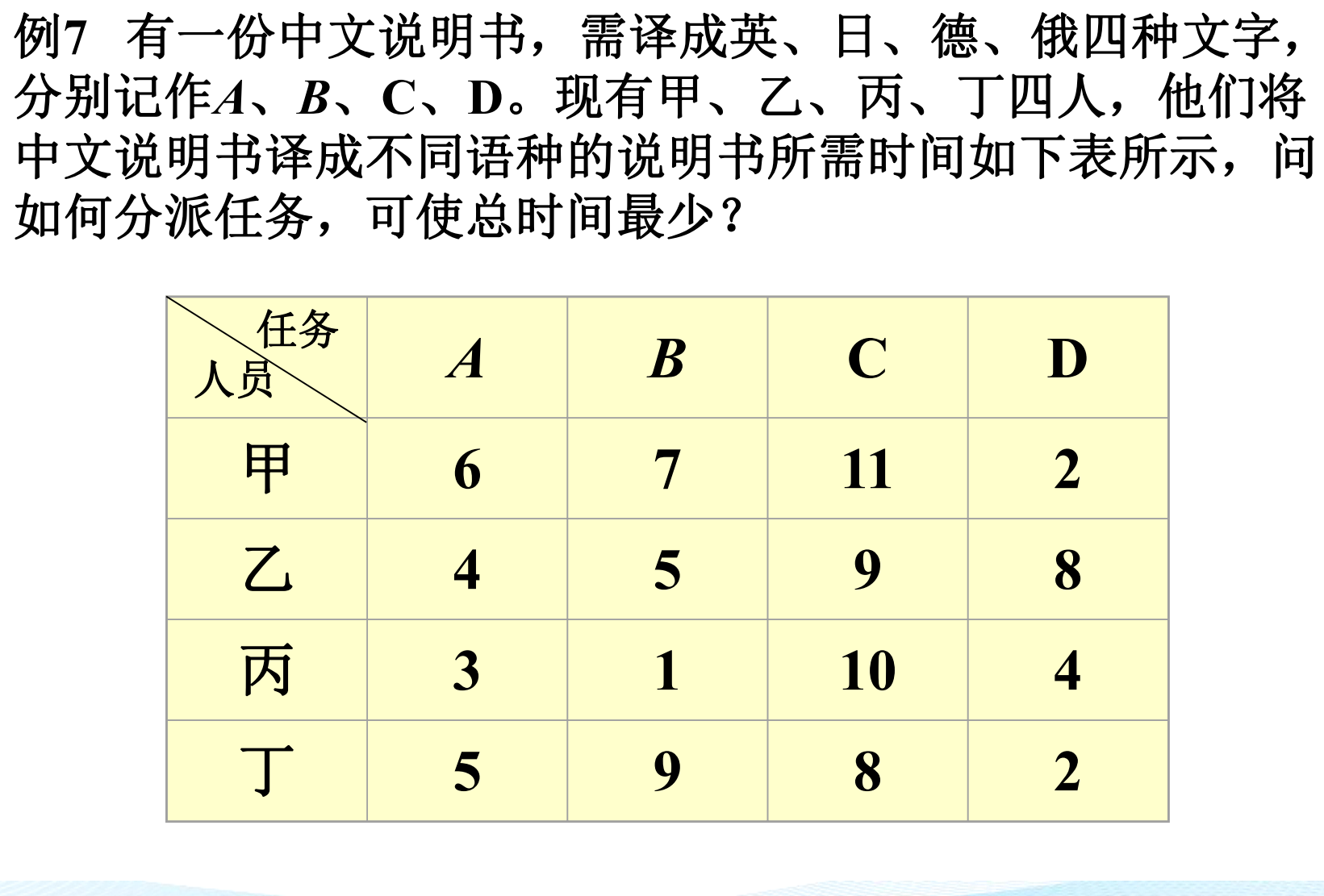
  1. 第一步：变换系数矩阵

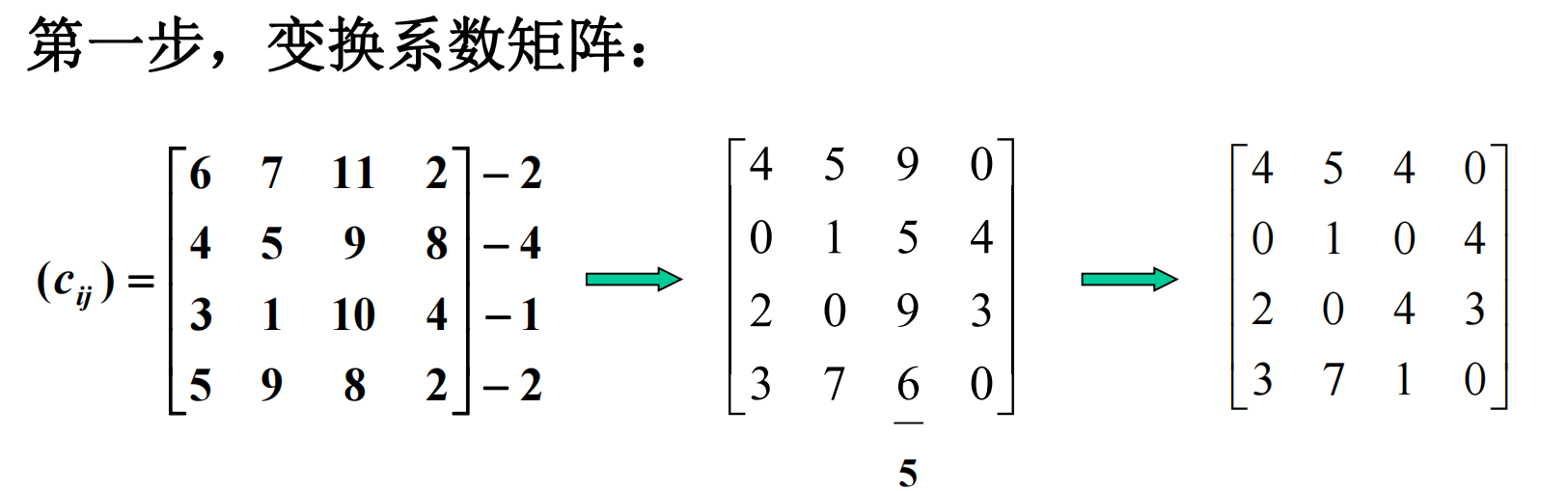
    变换系数矩阵

  2. 第二步：试指派

    试指派

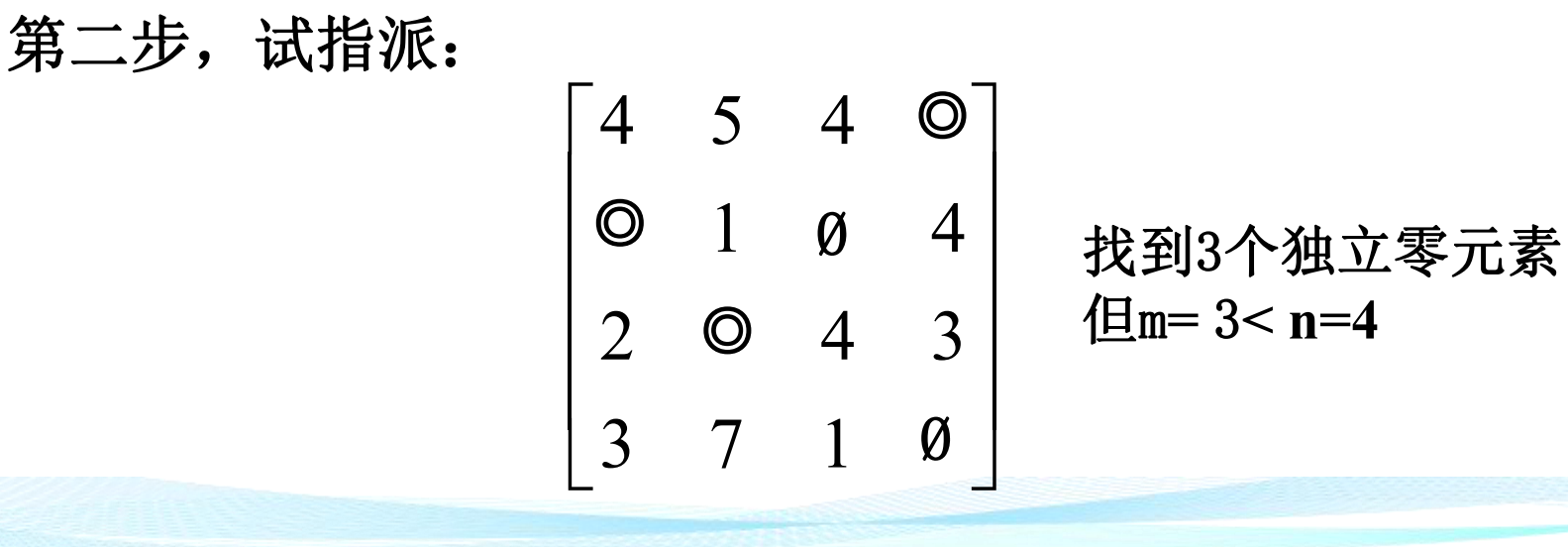
  3. 第三步：覆盖0元素

    覆盖0元素

  4. 第四步：变换系数矩阵，增加0元素

    变换系数矩阵

  5. 第二步：继续进行试指派

    试指派

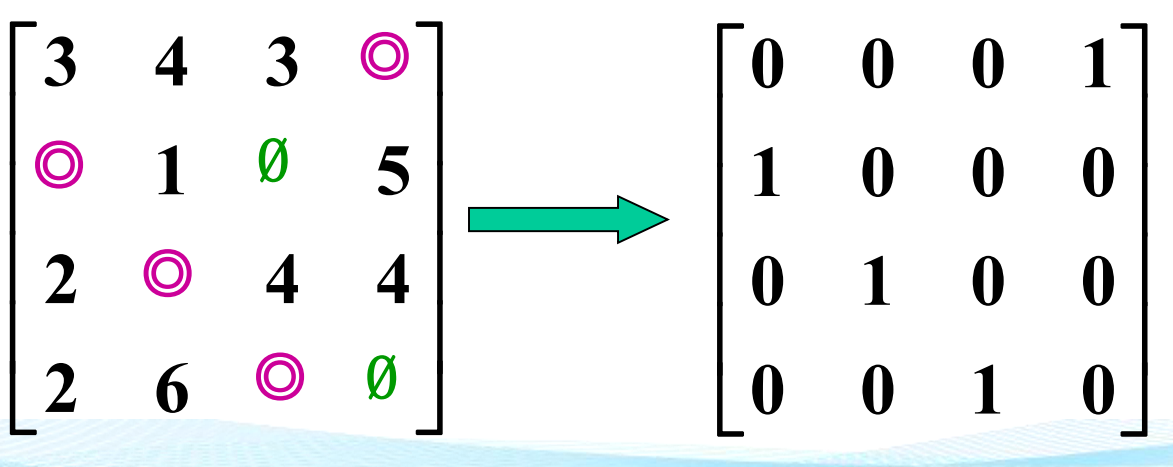
5. 01规划Python求解

以下内容参考博客：https://www.cnblogs.com/youcans/p/14854596.html

我们上面讲解了该如何使用匈牙利算法求解01规划问题，然而落实到真实的求解上，我们其实可以直接用PuLP即可，没有必要自己去写出来匈牙利算法，逼近CBC以及为我们准备好了。

下面以一个问题来进行举例

例题

A. 建模

定义决策变量

则模型为

B. Python求解

求解的具体过程我们其实还是使用PuLP库。类似于整数规划问题，我们只需要指定01变量的类别为”Binary”即可。

import pulp
import numpy as np


problem: pulp.LpProblem = pulp.LpProblem(name="最大化投资问题", sense=pulp.LpMaximize)


xs = np.array([pulp.LpVariable(name=f"x{i}", lowBound=0, cat=pulp.LpBinary) for i in range(5)])
profits = np.array([150, 210, 60, 80, 180])

contrain1 = np.array([1, 1, 1, 0, 0])
contrain2 = np.array([0, 0, 1, 1, 0])
contrain3 = np.array([-1, 0, 0, 0, 1])

problem.setObjective(profits @ xs)
problem += (contrain1 @ xs == 1, "约束1")
problem += (contrain2 @ xs <= 1, "约束2")
problem += (contrain3 @ xs <= 0, "约束3")

if pulp.LpStatus[problem.solve()] == "Optimal":
    v: pulp.LpVariable
    for v in problem.variables():
        print(f"{v.name}={v.varValue}")
    print(f"max Z={pulp.value(problem.objective)}")

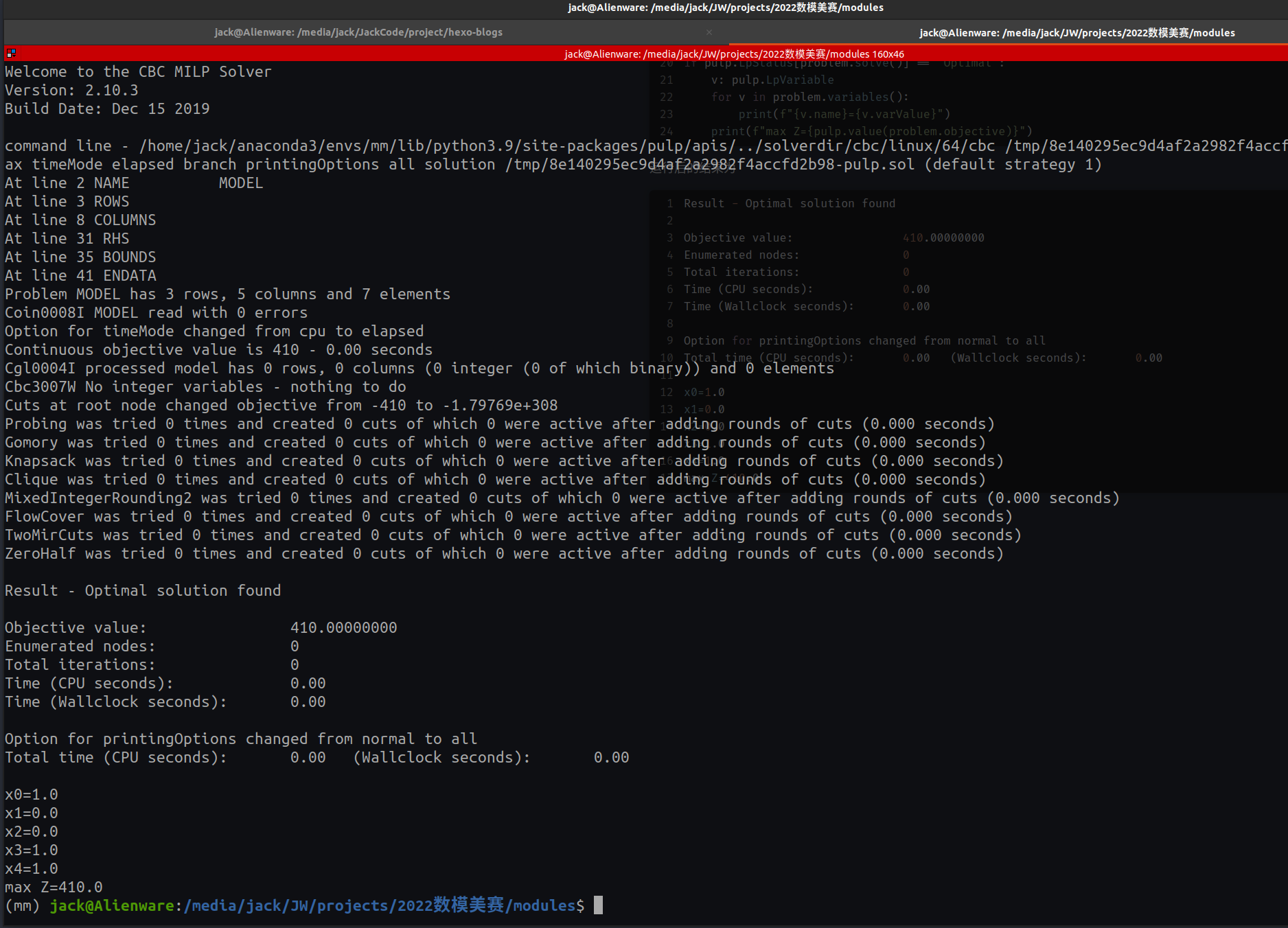
运行后的结果为

Result - Optimal solution found

Objective value:                410.00000000
Enumerated nodes:               0
Total iterations:               0
Time (CPU seconds):             0.00
Time (Wallclock seconds):       0.00

Option for printingOptions changed from normal to all
Total time (CPU seconds):       0.00   (Wallclock seconds):       0.00

x0=1.0
x1=0.0
x2=0.0
x3=1.0
x4=1.0
max Z=410.0

运行结果

文章作者: Jack Wang
文章链接: https://jackwang0107.github.io/2022/01/03/shu-xue-jian-mo-suan-fa-3-01-gui-hua/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Jack Wang !
Python Math Modeling Linear Programming 01规划
赏
  目录