本文是我CSDN中的文章,完成于2019年,现将其迁移到我的个人博客网站。本文主要介绍了Python中的推导式
This blog has been finished 2 years ago, in 2019, and was uploaded to CSDN. Now, this blog is transfer to my blog website.
Python推导式/Compression
推导式 ( Compression )是Python语言的一大特色:
相比于其他语言而言,推导式使得Python能够便捷的进行循环,创建出特定的字典、列表等可迭代对象
使用推导式可以避免代码的冗长,简化代码风格,使得代码更加的Pythonic
本文就将详细介绍Python中的推导式
推导式可以分为下面几种:
- 列表推导式
- 字典推导式
- 集合推导式
- 生成器推导式
1. List Comprehension
列表推导式指的是可以用于生成列表的推导式
A. Simple List Comprehension
简单的列表推导式的语法如下,这样我们就能够快捷的创建列表
[ 表达式 for 变量 in 可迭代对象 ]
示例如下
>>> List1=[x for x in 'abcd']
>>> List2=[y**2 for y in range(6)]
>>> List3=[i+1 for i in [-1,-2,-3,-4]]
>>> print(List1)
>>> print(List2)
>>> print(List3)
['a', 'b', 'c', 'd']
[0, 1, 4, 9, 16, 25]
[0, -1, -2, -3]
运行结果如下(In [1]中的内容可以不管)

B. List Comprehension with conditions
上面我们创建了简单的推导式,实际上还可以创建带条件的推导式,这样我们能够创建更复杂的表达式
带条件的列表推导式如下
[ 表达式 for 变量 in 可迭代对象 if 条件 ]
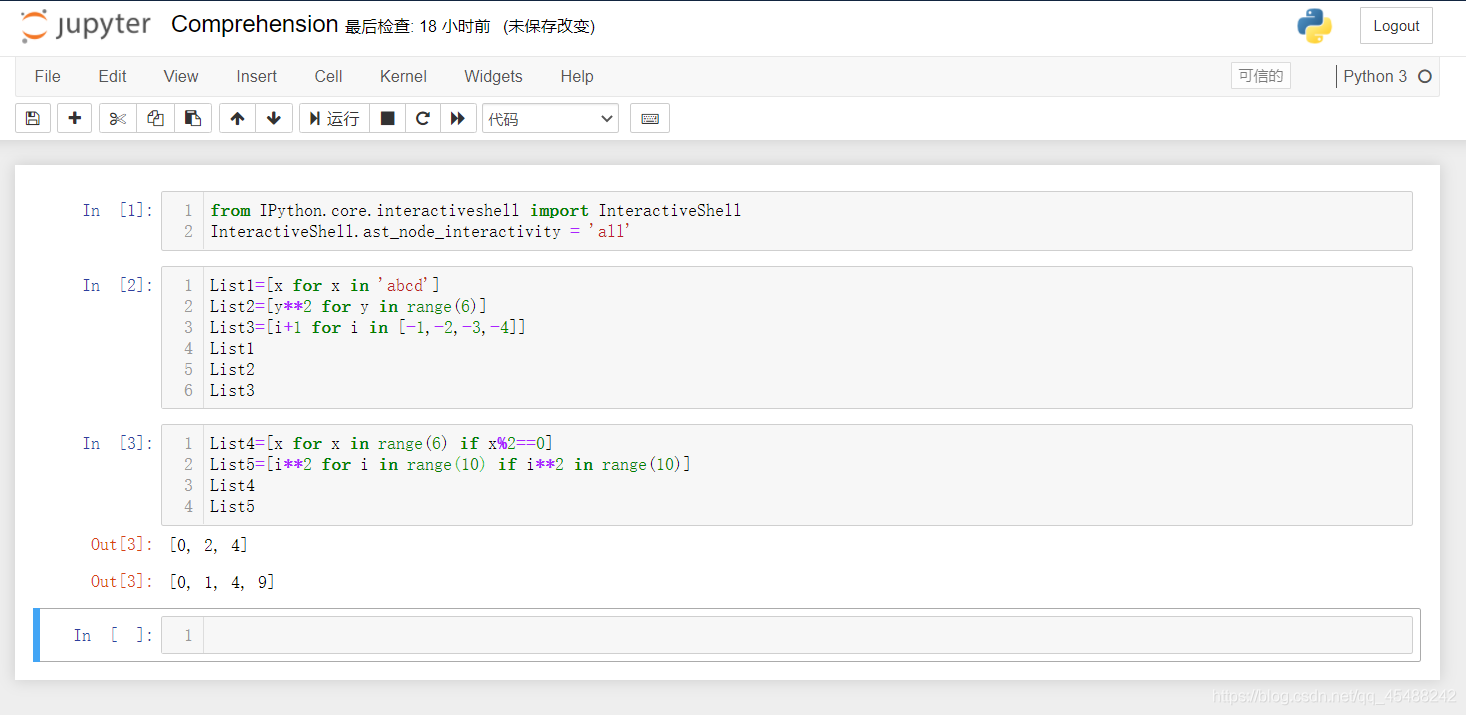
例子如下
>>>List4=[x for x in range(6) if x%2==0]
>>>List5=[i**2 for i in range(10) if i**2 in range(10)]
>>>print(List4)
>>>print(List5)
[0, 2, 4]
[0, 1, 4, 9]
C. Multi-variable Comprehension
我们前面的列表推导式实际上都只有一个变量,但是我们其实可以使用多变量的列表推导式
具体时候类似于两个for循环嵌套,因此又可以称为嵌套列表式/多变量推导式
以双变量和三变量为例的列表推导式如下, 按照这样的规则实际上可以扩展到n个变量的嵌套列表推导式
双变量列表推导式
[ 表达式(可含变量1和变量2) for 变量1 in 可迭代对象1 for 变量2 in 可迭代对象2 ]
三变量列表推导式
[ 表达式(可含变量1和变量及变量3) for 变量1 in 可迭代对象1 for 变量2 in 可迭代对象2 for 变量3 in 可迭代兑现3]
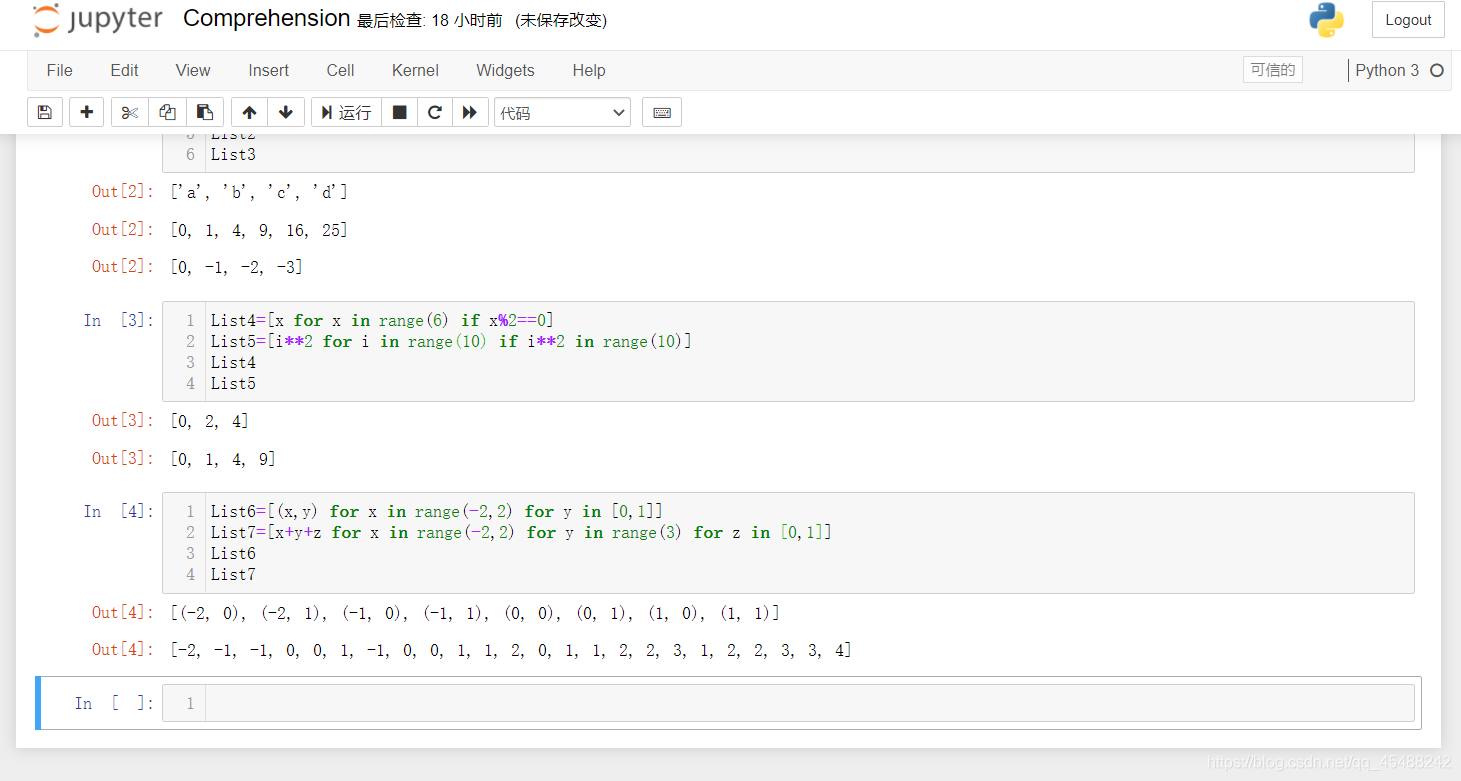
例子如下
>>> List6=[(x,y) for x in range(-2,2) for y in [0,1]]
>>> List7=[x+y+z for x in range(-2,2) for y in range(3) for z in [0,1]]
>>> print(List6)
>>> print(List7)
[(-2, 0), (-2, 1), (-1, 0), (-1, 1), (0, 0), (0, 1), (1, 0), (1, 1)]
[-2, -1, -1, 0, 0, 1, -1, 0, 0, 1, 1, 2, 0, 1, 1, 2, 2, 3, 1, 2, 2, 3, 3, 4]
运行结果如下

C. Complex Comprehension
实际上我们能够结合带条件的列表推导式和嵌套列表推导式,由此可以有一些非常Pythonic的操作
>>>List8=[(x,y) for x in range(-20,20,1) for y in range(-20,20,1) if y==x**2 ]
>>>print(List8)
[(-4, 16), (-3, 9), (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4), (3, 9), (4, 16)]
上面的代码就是求y=x**2的曲线上的点的代码
其实后续结合Numpy,Pandas,Matplotlib等诸多第三方库还可以进行绘图,
此外还能通元组赋值, zip和enumerate等函数产生妙用
具体就不一一细讲了,总之列表作Python中最常用的结构型数据类型, 列表推导式的妙用非常多
2. Dictionary Comprehension
类似于列表推导式, 字典推导式也可以结合条件语句以及多变量嵌套
A. Simple Dictionary Comprehension
简单的字典推导式只使用一个变量, 因此键和键值的表达式中都需要有变量
声明语句如下
{ 键表达式 : 值表达式 for 表达式 in 可迭代对象 }
举例如下
>>>Dict1={i : i**2 for i in range(6)}
>>>print(Dict1)
{0: 0, 1: 1, 2: 4, 3: 9, 4: 16, 5: 25}

B. Multi-Variable Dictionary Comprehension
实际上一般在创建字典的时候,我们使用的键和键值是不一样的,因此我们更常见的做法是使用嵌套的字典推导式/多变量字典推导式, 即使用多个变量分别作为键和值来进行循环,这样来创建不同的键值对
{ 键表达式 : 值表达式 for 变量1 in 可迭代对象1 for 变量2 in 可迭代对象2 }
示例如下:
Dict1={letter : i for i in range(6) for letter in "abcdef"}
Dict1
>>>
{'a': 5, 'b': 5, 'c': 5, 'd': 5, 'e': 5, 'f': 5}

C. Dictionary Comprehension with conditions
其实和嵌套的字典推导式一样,略
D. Complex Dictionary Comprehension
复杂字典推导式能够实现各种骚气的功能
具体就不细说了,我下面给一个例子,更多的使用还需要大家自己开发
>>> Sentece='This is a sentence waiting to be count that how many times does letters occur in this sentence'
>>> Dict2={letter : Sentece.lower().count(letter) for letter in list('abcdefghijklmnopqrstuvwxyz') }
>>> import pprint
>>> pprint.print(Dict2)
{'a': 4,
'b': 1,
'c': 5,
'd': 1,
'e': 11,
'f': 0,
'g': 1,
'h': 4,
'i': 7,
'j': 0,
'k': 0,
'l': 1,
'm': 2,
'n': 8,
'o': 5,
'p': 0,
'q': 0,
'r': 2,
's': 8,
't': 12,
'u': 2,
'v': 0,
'w': 2,
'x': 0,
'y': 1,
'z': 0}
这个例子的作用就是查询这一句话中26个字母出现的字数,可以看到在C/C++中需要写很多行代码才能实现的功能在Python中只需要一行就能结束
3. 集合推导式
集合推导式和列表推导是一样的,三种用法都一样,就不赘述了
{ 表达式 for 表达式 in 可迭代变量}
例子如下:
Set1={x for x in range(6)}
Set1
>>>
{0, 1, 2, 3, 4, 5}