本文主要讲解了数学建模中常见的一类问题：整数规划，及其求解

数学建模算法2-整数规划

在上一篇文章中，我们介绍了线性规划问题及其算法求解。线性规划问题的关键就在于：

1. 有限的资源（写出来约束）
2. 最大化价值（写出来目标函数）

判断一个问题是否可以通过线性规划求解就是看这个问题是否通过划归而具有上面的两个特点。

线性规划其实有一个隐含的条件，就是要求决策变量（需要通过线性规划决策值的变量）是连续的。但是在现实中，并不所有线性规划问题的决策变量都是连续的，有的时候，我们的决策变量是一个整数。

例如任务指派问题，在有限的人数的情况下尽可能少的派人去完成问题，这个问题符合上面的两个特点。但是其决策变量人数并不是一个连续的变量，因此直接套用线性规划是不行的。那么可能就会有人要问了，线性规划给出的小数解可能不符合要求，那么取整不就可以了？

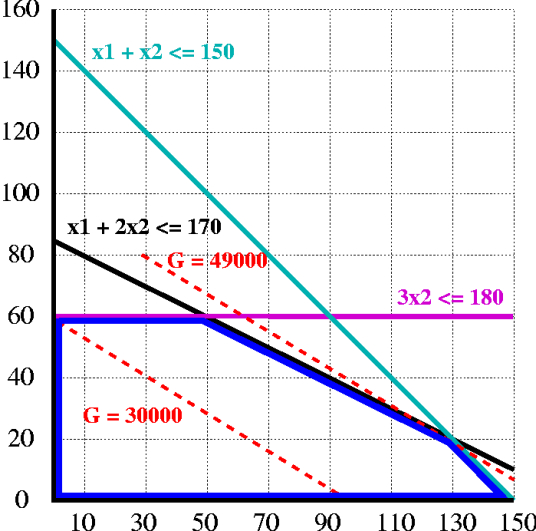
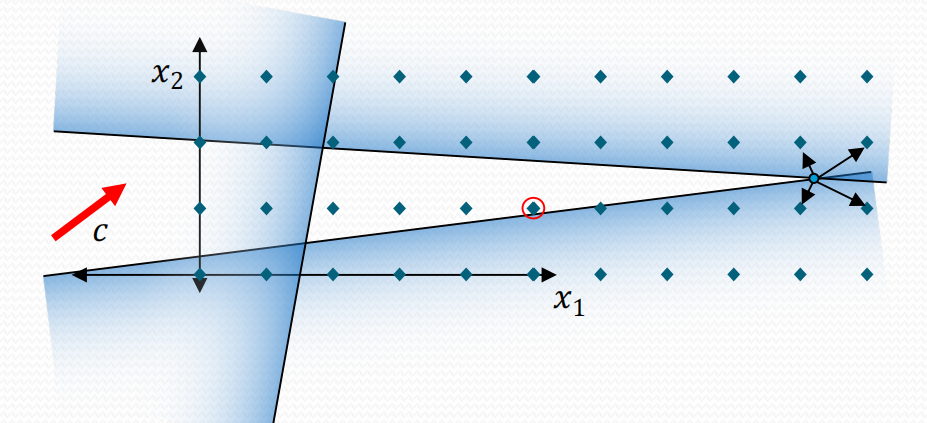
但其实简单的取整是不能处理所有的这样的问题的，例如封面图：线性规划给出的最优解是右侧的点，对这个点的x、y坐标无论怎样取整，得到的解都不在可行域内，甚至周围几个点也都不在可行域内。因此针对这类问题我们为他们取了一个名字：整数规划（Integer Programming，IP），并对整数问题的求解方法进行研究。

1. 整数规划的发展历史

上面的lead-in其实已经相当于介绍了，那么这里就介绍一下整数规划的发展历史吧。

整数规划是从1958年由R.E.戈莫里提出线性规划的割平面法之后形成独立分支的 ，30多年来发展出很多方法解决各种问题。解整数规划最典型的做法是逐步生成一个相关的问题，称它是原问题的衍生问题。对每个衍生问题又伴随一个比它更易于求解的松弛问题（衍生问题称为松弛问题的源问题）。通过松弛问题的解来确定它的源问题的归宿，即源问题应被舍弃，还是再生成一个或多个它本身的衍生问题来替代它。随即 ，再选择一个尚未被舍弃的或替代的原问题的衍生问题，重复以上步骤直至不再剩有未解决的衍生问题为止。现今比较成功又流行的方法是分支定界法和割平面法，它们都是在上述框架下形成的。

需要注意的是，目前对于整数规划并不存在求解一切整数规划问题的方法（二次的约束、不连续的约束），目前流行的求解方法往往只适用于线性整数规划

2. 整数规划的定义

通过上面的介绍，我们应该明白了什么是整数规划，即决策变量是整数的规划问题。如果规划的约束和目标函数都是线性的话，则称为线性整数规划。考虑到我们在数学建模的过程中往往都是对线性整数规划进行的求解，因此我们也把线性整数规划简称为整数规划，并且在后文中如果我们没有特地声明，那么所说的整数规划统统指线性整数规划

上面是我们主观的理解，下面给出百度百科和维基百科上的定义：

From BaiduBaike：

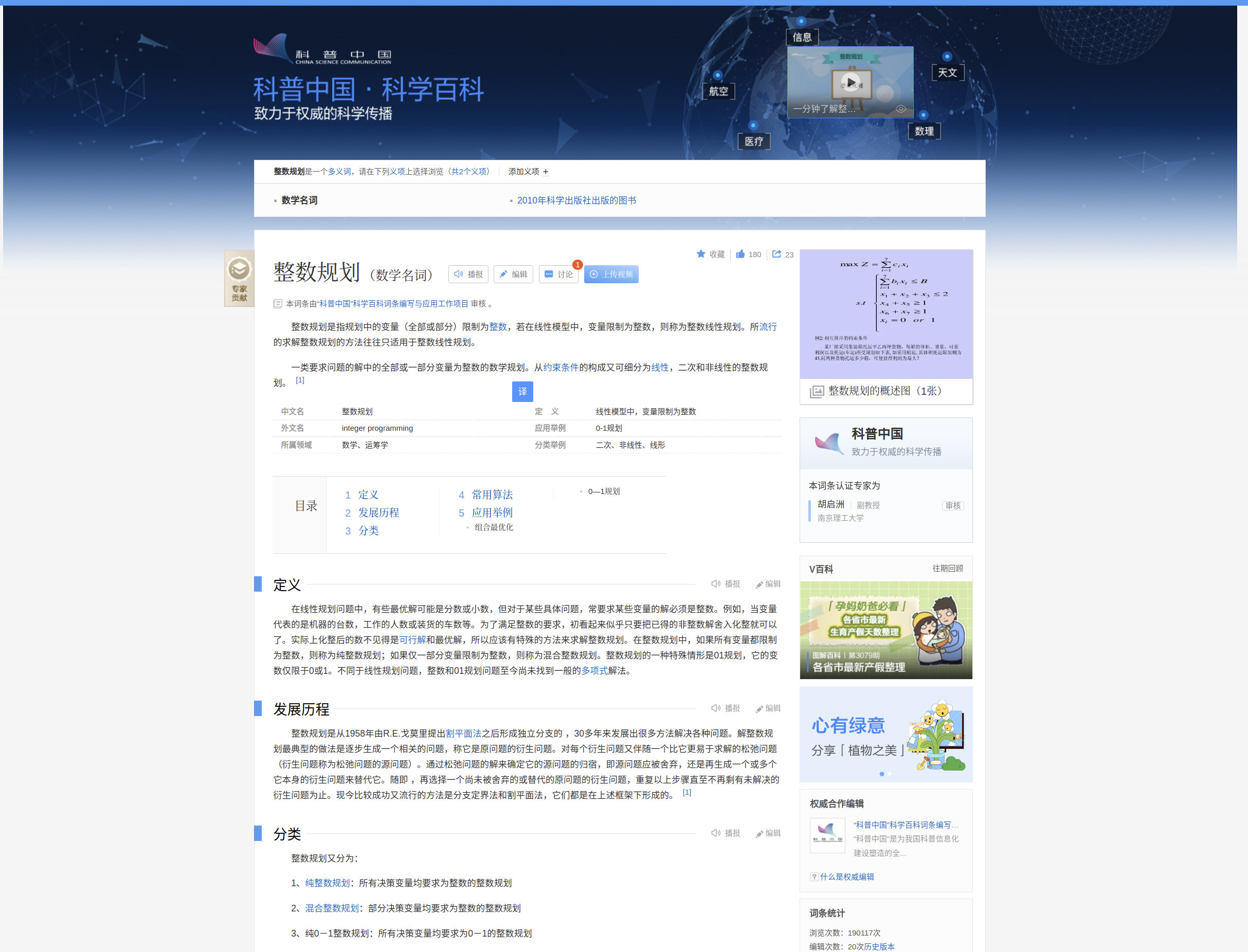
整数规划是指规划中的变量（全部或部分）限制为整数，若在线性模型中，变量限制为整数，则称为整数线性规划。所流行的求解整数规划的方法往往只适用于整数线性规划。
一类要求问题的解中的全部或一部分变量为整数的数学规划。从约束条件的构成又可细分为线性，二次和非线性的整数规划。

From Wikipedia：

PS: 维基百科没有针对整数规划的词条。整数规划的定义在线性规划词条下。

要求所有的未知量都为整数的线性规划问题叫做整数规划（integer programming, IP）或整数线性规划（integer linear programming, ILP）问题。

3. 整数规划的分类

针对问题中决策变量的不同，整数规划可以分为下面的几类：

• 纯整数规划（Pure Integer Programming，PIP）：所有的决策变量要求都是整数的整数规划，但是为解决问题引入的松弛变量或者剩余变量不要求取整

松弛变量与剩余变量：

在求解多变量不等式问题的时候，通常形式是这样的：$x_1+x_2\leq 10$；有的时候为了便于求解，希望能够减少不等式中的变量个数。因此针对上式，引入第三个变量$x_3$，使得$x_1+x_2+x_3=10$，则原不等式变换为一个等式和一个单变量不等式$x_3\ge 0$。

此时称变量$x_3$为松弛变量。直观的理解就是$=$是更加严格的条件，而变量$x_3$让严格的条件松弛称为需要求解问题。

此外，若$x_1+x_2\ge 10$，则引入变量$x_3$，使得$x_1+x_2-x_3=10$，则$x_3\ge0$，此时称$x_3$为剩余变量。即比要求的$=10$多出来的部分

• 混合整数规划（Mixed Integer Programming，MIP）：部分决策变量均要求为整数的整数规划
• 纯0－1整数规划（Pure 0-1 Integer Programming）：所有决策变量均要求为0－1的整数规划
• 混合0－1规划（Mixed 0-1 Integer Programming）：部分决策变量均要求为0－1的整数规划

4. 整数规划和线性规划的关系

A. 解之间的关系

整数规划实际上是线性规划的一个特例，即在正常的线性规划上加上了非线性的整数约束。因此，根据线性规划解的特点，可以得到整数规划和线性规划解之间的关系：

• 最优解一致：整数规划去掉整数约束后的线性规划（称为伴随问题或者松弛问题）的最优解为整数，那么整数规划与线性规划的最优解一致。
• 最优解变差：整数规划的伴随问题的最优解是小数，且整数规划存在可行解，那么整数规划的存在最优解，只是最优解相比伴随问题的最优解变差
• 无最优解：伴随问题可行域内无整数解，故整数规划可能没有最优解

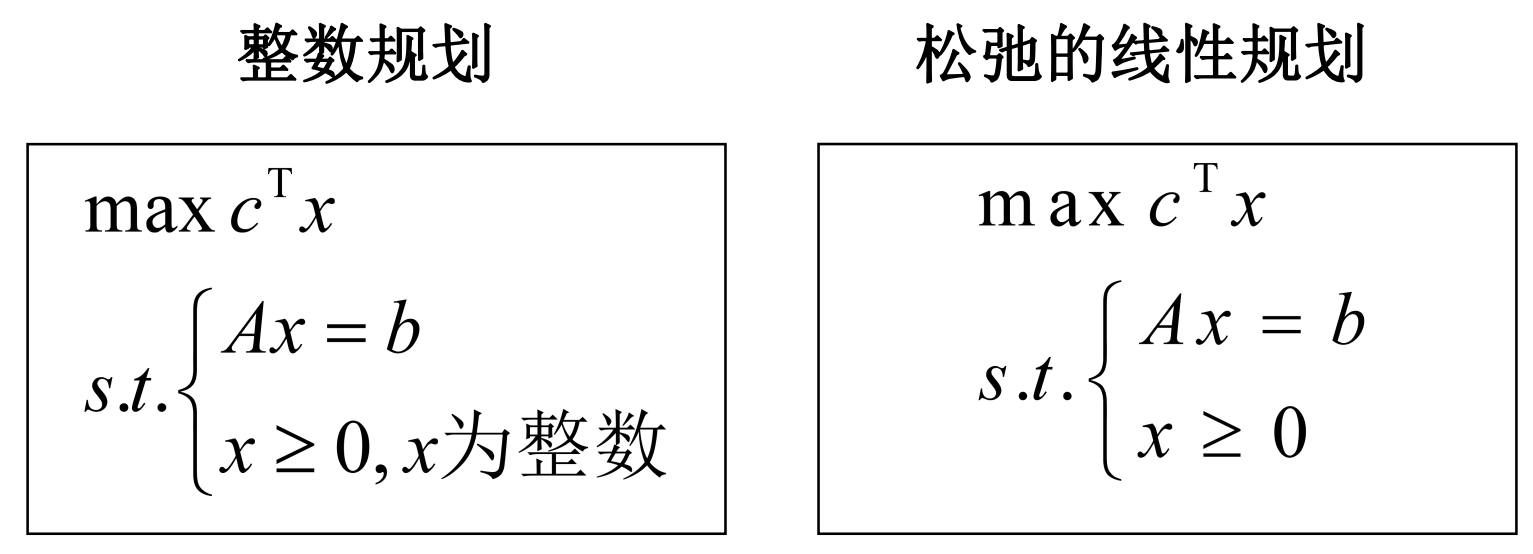
B. 标准形式的关系

由于整数规划只是给决策变量多加了一个要求是整数的这个约束，因此两者的标准式之间基本没有差别

5. 适合整数规划求解的问题

A. 合理下料问题

设用某型号的圆钢可以用于生产零件$A_1$， $A_2$，……，$A_m$ 。在一根圆钢上下料（切割）的方式有$B_1$，$B_2$，……，$B_n$ 种，每种下料方式可以得到各种零件的毛坯数以及用于生产的每种零件的需要量，如下表所示。问怎样安排下料方式，使得在满足生产需要的同时所用的圆钢数量最少？

上面这个问题，需要的零件作为受限的资源，需要收益（消耗的圆钢）最少因此是一个数学规划问题

设$x_j$表示用$B_j$种下料方式生产的圆钢，则此时问题的数学模型为：

$$\min_{x_1,\cdots,x_n}z = \sum_{j=1}^n x_j\\ \begin {cases} \sum_{j=1}^n {a_{ij}x_j} \ge b_i &i=1,\cdots,n\\ x_j \ge 0, &i=1,\cdots,n\\ x_j为整数 \end {cases}$$

B. 建厂问题

某公司计划在m个地点建厂，可供选择的地点有$A1$，$A_2$，……，$A_m$ ，在这些地点建立的工厂的生产能力分别是$a_1$， $a_2$，……，$a_m$（假设生产同一产品）。第 $i$个工厂的建设费用为$f_i,\ i=1,2,\cdots,m$。又有 $n$ 个地点$B_1$，$B_2$，……，$B_n$ 需要销售这 种产品，其销量分别为$b_1$，$b_2$，……，$b_n$ 。从工厂运往销地的单位运费为$c{ij}$。试决定应在哪些地方建厂，既可以满足各地需要，又使总建设费用和总运输费用最少？

同样，销量是限制的资源，而总费用作为收益需要最优，因此是一个规划问题

根据题意，可以列出下表

设$x_{ij}$为从工厂$i$运往销地$j$的运输量（$i=1,\cdots,m;j=1,\cdots n$），另设

$$Y_{ij}= \begin{cases} 1, &在A_i处建厂\\ 0, &不在A_i处建厂 \end{cases}$$

则建厂问题数学模型为:

$$\min_{x_{ij},y_i} Z=\sum_{j=1}^m\sum_{i=1}^nc_{ij}x_{ij}+\sum_{i=1}^mf_iy_i\\ \begin {cases} \sum_{j=1}^n x_{ij} \leq a_iy_i,&i=1,\cdots,m\\ \sum_{i=1}^m x_{ij} \ge b_j, &j=1,\cdots,n\\ x_{ij}\ge 0, &i=1,\cdots,m;j=1,\cdots,n\\ y_i=1或y_i=0, &i=1,\cdots,m \end{cases}$$

6. 整数规划的求解

从数学模型上看整数规划似乎是线性规划的 一种特殊形式，求解只需在线性规划的基础上， 通过四舍五入取整，寻求满足整数要求的解即可。 但实际上两者却有很大的不同，通过四舍五入有得到的整数解也不一定就是最优解，有时甚至不能保证所得到的解是整数可行解。

因此，针对整数规划就有了其他的求解算法。目前，对于求解整数规划常用的方法有：分支定界法和割平面法；对于0-1规划问题，常用的算法有隐枚举法和匈牙利算法

A. 分支定界算法

分支定界算法的基本就是当作为松弛问题的线性规划问题的解为整数解的时候，整数规划的最优解就是松弛问题的最优解

因此，分支定界算法的基本思想就是不断地对可行域进行划分（每次划分可行域实际上是添加新的约束），然后对所有的子可行域进行线性规划直到找到解为整数的解，此时该解可能为整数规划的一个最优解。

算法的自然语言描述如下：

• 首先不考虑整数限制先求出相应松弛问题的最优解$\vec x=[x^0_1, \cdots, x^0_n]$

  • 若松弛问题无可行解，则ILP无可行解

  • 若求得的松弛问题最优解符合整数要求，则是ILP的最优解

  • 若不满足整数条件，则从最优解中选择一个不满足整数条件的变量，对其构造新的约束添加到松弛问题中形成两个子问题
    添加的新的约束为

    $$x_i\leq \lfloor x^0_i\rfloor或者x_i \ge \lceil x^0_i\rceil$$

  • 依次在缩小的可行域中求解新构造的线性规划的最优解

• 重复上述过程，直到子问题无解或有整数最优解（被查清）

算法流程图如下：

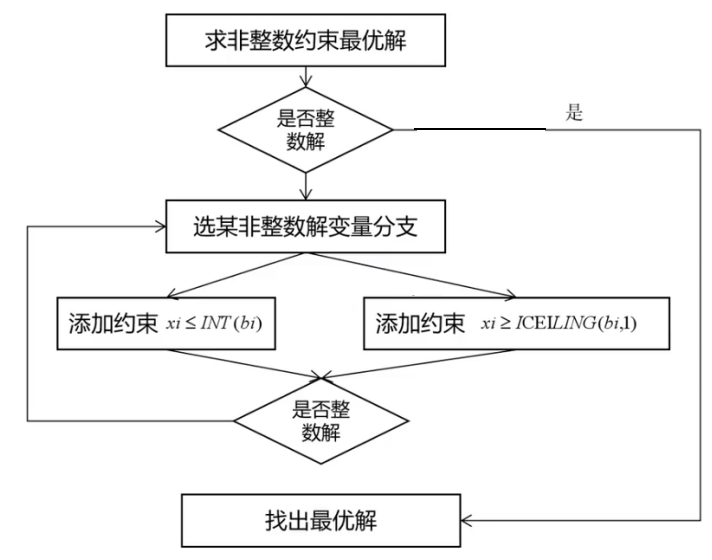
下面结合两个个例子来讲解分支定界算法

求下面的整数规划问题

$$\max_{x_1, x_2} z=3x_1+2x_2\\ \begin {cases} 2x_1+3x_2 \leq 4\\ 2x_1+x_2 \leq 24\\ x_1, x_2 \ge 0\\ x_1, x_2为整数 \end{cases}$$

求解步骤如下：

1. 求解松弛问题的解

   $$\max_{x_1, x_2} z=3x_1+2x_2\\ \begin {cases} 2x_1+3x_2 \leq 4\\ 2x_1+x_2 \leq 24\\ x_1, x_2 \ge 0\\ \end{cases}$$

   得

   $$\begin {cases} x_1=3.25\\ x_2=2.5\\ z_{max}=14.75\\ \end{cases}$$

   此时松弛问题有解，但是决策变量$x_1$，$x_2$都不是整数，因此对两个变量每个都要添加新的约束

2. 首先对决策变量$x_1$添加约束

   $$\max_{x_1, x_2} z=3x_1+2x_2\\ \begin {cases} 2x_1+3x_2 \leq 4\\ 2x_1+x_2 \leq 24\\ x_1\le 3\\ x_1, x_2 \ge 0\\ \end{cases}$$

   求解，得

   $$\begin {cases} x_1=3\\ x_2=2.67\\ z_{max}=14.33\\ \end{cases}$$

   添加另外一种约束

   $$\max_{x_1, x_2} z=3x_1+2x_2\\ \begin {cases} 2x_1+3x_2 \leq 4\\ 2x_1+x_2 \leq 24\\ x_1\ge 4\\ x_1, x_2 \ge 0\\ \end{cases}$$

   求解得到第一个可能的解

   $$\begin {cases} x_1=4\\ x_2=1\\ z_{max}=14\\ \end{cases}$$

3. 接下来对决策变量$x_2$添加约束

   $$\max_{x_1, x_2} z=3x_1+2x_2\\ \begin {cases} 2x_1+3x_2 \leq 4\\ 2x_1+x_2 \leq 24\\ x_1\le 3\\ x_2\leq 2\\ x_1, x_2 \ge 0\\ \end{cases}$$

   得到一个可能的解

   $$\begin {cases} x_1=3\\ x_2=2\\ z_{max}=13\\ \end{cases}$$

   然后添加另外一种约束

   $$\max_{x_1, x_2} z=3x_1+2x_2\\ \begin {cases} 2x_1+3x_2 \leq 4\\ 2x_1+x_2 \leq 24\\ x_1\le 3\\ x_2\ge 3\\ x_1, x_2 \ge 0\\ \end{cases}$$

   得到解

   $$\begin {cases} x_1=2.2\\ x_2=3\\ z_{max}=13.5\\ \end{cases}$$

4. 接下来重复步骤，直到所有的子问题的子问题的解都是整数解或者无解

最终通过对所有的可能的解进行比较，得到最终的解为

$$\begin {cases} x_1=4\\ x_2=1\\ z_{max}=14\\ \end{cases}$$

再举一个例子

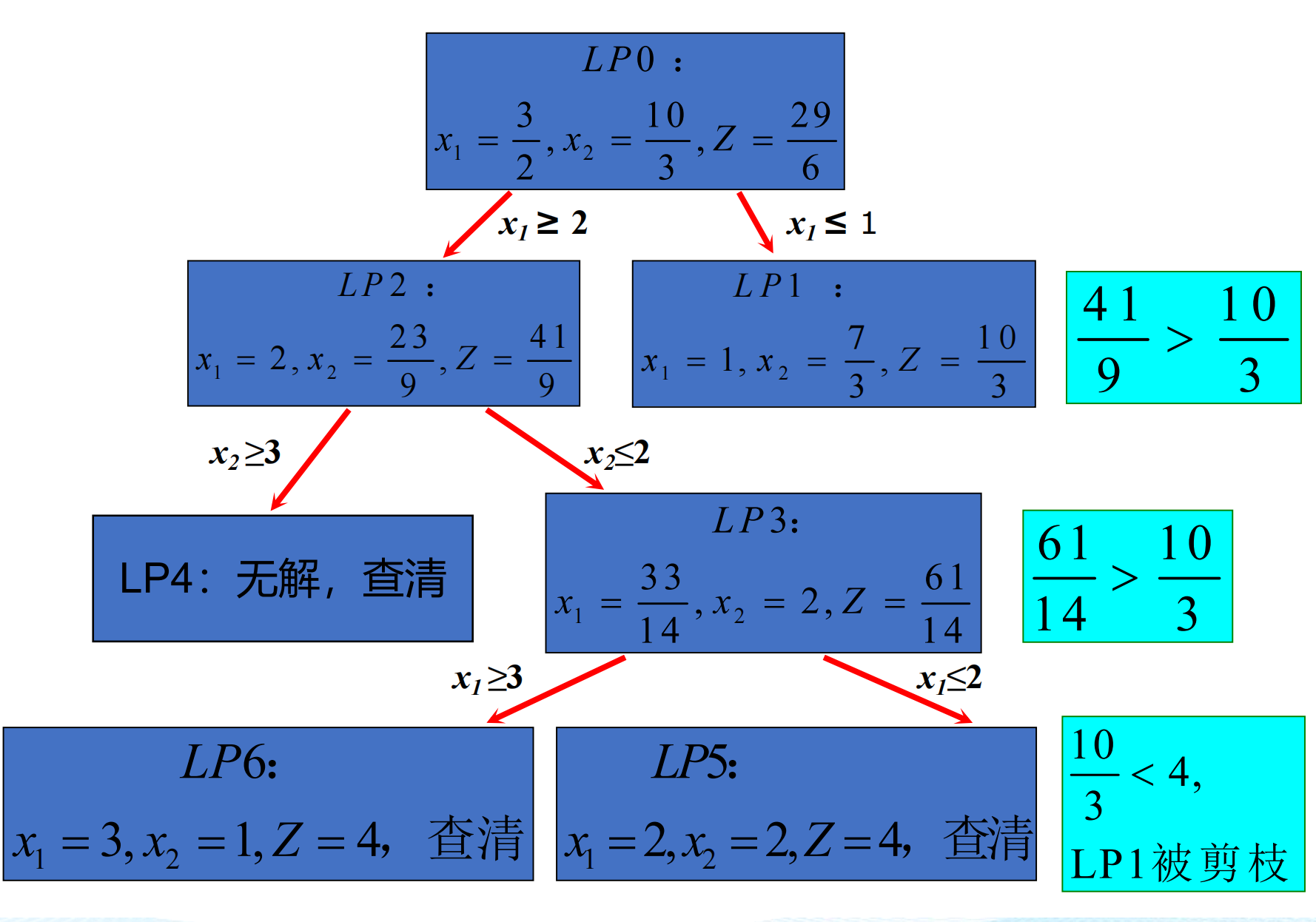
求下面的整数规划的解

$$\max_{x_1, x_2} z=x_1+x_2\\ \begin {cases} x_1+\frac9{14}x_2 \leq \frac{51}{14}\\ -2x_1+x_2 \leq \frac 1 3\\ x_1, x_2 \ge 0\\ x_1, x_2为整数 \end{cases}$$

同样，类似于上面的不断添加约束，最后得到一个搜索树，注意下面这个是深度优先的搜索树

B. 割平面算法

割平面算法的核心思想就是：

1. 对线性规划问题P添加约束等价于进一步缩小可行域（割去可行域）
2. 对松弛问题P不断添加约束条件，即可行域不断地割去一块，使得非整数解恰好在割去的区域中而没有割去原问题的可行解，得到新问题P’
3. 对问题P’继续进行线性规划，直到
   1. 松弛问题无解，则整数规划问题无解
   2. 松弛问题最优解为整数向量，则整数规划的解就是松弛问题的解

下面结合一个例子讲解割平面算法

求下面的整数规划

$$\max_{x_1,x_2}z=x_1+x_2\\ \begin{cases} -x_1+x_2\leq 1\\ 3x_1 +x_2 \leq4\\ x_1, x_2 \ge 0\\ x_1, x_2均为整数 \end{cases}$$

上面这个例子的可行域如下，松弛问题的最优解为$(\frac 43,\frac34)$，因此对其进行分割。

割平面算法要求分割的时候分割的区域不能包含整数解，因此选择分割的两个区域为上边和右边的两个蓝色三角形。

对这两个区域进行分割后（添加约束后），新的问题P’为

$$\max_{x_1,x_2}z=x_1+x_2\\ \begin{cases} -x_1+x_2\leq 1\\ 3x_1 +x_2 \leq4\\ x_1, x_2 \ge 0\\ x_1\leq 1\\ x_2\leq 1\\ x_1, x_2均为整数 \end{cases}$$

此时对P’的松弛问题进行求解，得到解为

$$\begin {cases} x_1=1\\ x_2=1\\ z_{max}=2\\ \end{cases}$$

此时松弛问题的解为整数解，因此算法结束。

因此，割平面算法最关键的步骤就是在于判断该怎样对平面进行切割。具体来说进行切割的方法为引入松弛变量和剩余变量。这里就不再展开了。

7. 整数规划的Python求解

虽然我们上面介绍了如何在线性规划的基础上对整数规划问题进行求解的算法。但其实我们并不需要自己动手实现他们。正如我们前面所说的，数学建模的目的在于运用这个算法去解决实际问题而非去动手显示这些算法。

对整数规划问题进行求解，我们当然可以在前面介绍的SciPy的linprog的基础上自己动手实现这些算法，然而其实有其他的库已经帮助我们进行了这一步了，因此我们直接调用即可。

具体来说，这个库就是PuLP库，这是他的官网：https://coin-or.github.io/pulp/index.html

从原理上来说，PuLP这个库是基于其他的线性规划求解程序，在PuLP这个库来说，这些求解线性规划的程序称为求解器。求解器提供了命令行的接口和API，因此PuLP其实就是对这些API做了一层Python Binding，从而实现的在Python中求解整数规划问题。

PuLP中默认的求解器是开源的CBC求解器，此外还支持很多其他的开源或者商业的求解器。不过CBC用来解决我们一般的几百个决策变量的规划问题肯定是足够了。

下面针对下面这个线性规划问题使用PuLP进行求解

$$\max_{x_1, x_2} z=x_1+x_2\\ \begin {cases} x_1+\frac9{14}x_2 \leq \frac{51}{14}\\ -2x_1+x_2 \leq \frac 1 3\\ x_1, x_2 \ge 0\\ x_1, x_2为整数 \end{cases}$$

A. 定义问题

PuLP求解线性规划问题第一步就是创建一个线性规划问题（Linear Program Problem，LpProblem）。PuLP中将线性规划问题抽象为一个类，而诸如约束条件、优化目标、决策变量等等都是该类下的属性

import pulp

problem: pulp.LpProblem = pulp.LpProblem(name="线性规划例子", sense=pulp.LpMaximize)

我们在初始化该类的时候需要指定该问题的名称，以及优化的类型，是最大值还是最小值

B. 创建决策变量

同样，决策变量也被抽象为了一个类，因此我们需要对其进行初始化

x1 = pulp.LpVariable(name="x1", cat=pulp.LpInteger, lowBound=0)
x2 = pulp.LpVariable(name="x2", cat=pulp.LpInteger, lowBound=0)

我们在创建决策变量的时候首先需要指定决策变量的名称，然后指定其类型，因为我们要求解的整数规划问题，因此我们指定这两个变量的取值是整数。

此外我们还指定了这两个变量的下界都是0，类似与SciPy中连续的线性规划，我们不指定上界（上届为None）的时候，默认是无穷

C. 设置优化目标和约束

我们设置优化目标和添加约束的时候，既可以通过LpProblem类的接口显示的添加，也可以通过其重载的运算符完成

problem.setObjective(x1 + x2)

problem += x1 + 9/14 * x2 <=51/14, "约束1"
problem += pulp.LpConstraint(e=(-2 * x1 + x2), sense=pulp.LpConstraintLE, rhs=1/3, name="约束2")
# problem += -2 * x1 + x2 <= 1/3, "约束2"

上面我们设定优化目标是$x_1+x_2$，然后分别通过problem重载的+=符号、提供的类进行约束添加

我们此时可以打印一下problem，就能够看到添加了目标和约束之后的问题

>>> print(problem)
线性规划例子:
MAXIMIZE
1*x1 + 1*x2 + 0
SUBJECT TO
约束1: x1 + 0.642857142857 x2 <= 3.64285714286

约束2: - 2 x1 + x2 <= 0.333333333333

VARIABLES
0 <= x1 Integer
0 <= x2 Integer

D. 求解

由于并不是所有的问题都是可解的因此在对问题进行求解后，实际上问题会有很多种状态，所有的解的状态保存在pulp.LpStatus这个常量中

>>> import pprint
>>> pprint.print(pulp.LpStatus)
{-3: 'Undefined',
 -2: 'Unbounded',
 -1: 'Infeasible',
 0: 'Not Solved',
 1: 'Optimal'}

其中，

• Optimal表示已经得到了最优解
• Not Sloved，即problem在求解前的状态
• Infeasible，即问题不存在可行解，例如我们的约束中出现了$2\leq x \leq -1$这样的条件
• Unbounded，即得到的答案是无穷，例如优化目标为$z=3x$，而约束为$1\leq x$
• Undefined，即问题可能存在最优解，但是求解器的求解算法没有得出解

因此，在我们对问题求解之后，只有Optimal才会得到最终的答案，所以我们求解结束之后输出的时候需要检查一下状态

print(problem)

if pulp.LpStatus[status] == "Optimal":
    variable: pulp.LpVariable
    for variable in problem.variables():
        print(f"{variable.name}={variable.varValue}")
    print(pulp.value(problem.objective))

E. 完整代码

完整代码如下

import pulp

problem: pulp.LpProblem = pulp.LpProblem(name="线性规划例子", sense=pulp.LpMaximize)

x1 = pulp.LpVariable(name="x1", cat=pulp.LpInteger, lowBound=0)
x2 = pulp.LpVariable(name="x2", cat=pulp.LpInteger, lowBound=0)

problem.setObjective(x1 + x2)

problem += x1 + 9/14 * x2 <=51/14, "约束1"
problem += pulp.LpConstraint(e=(-2 * x1 + x2), sense=pulp.LpConstraintLE, rhs=1/3, name="约束2")
# problem += -2 * x1 + x2 <= 1/3, "约束2"


status = problem.solve()

# print(status)
print(problem)

if pulp.LpStatus[status] == "Optimal":
    variable: pulp.LpVariable
    for variable in problem.variables():
        print(f"{variable.name}={variable.varValue}")
    print(pulp.value(problem.objective))

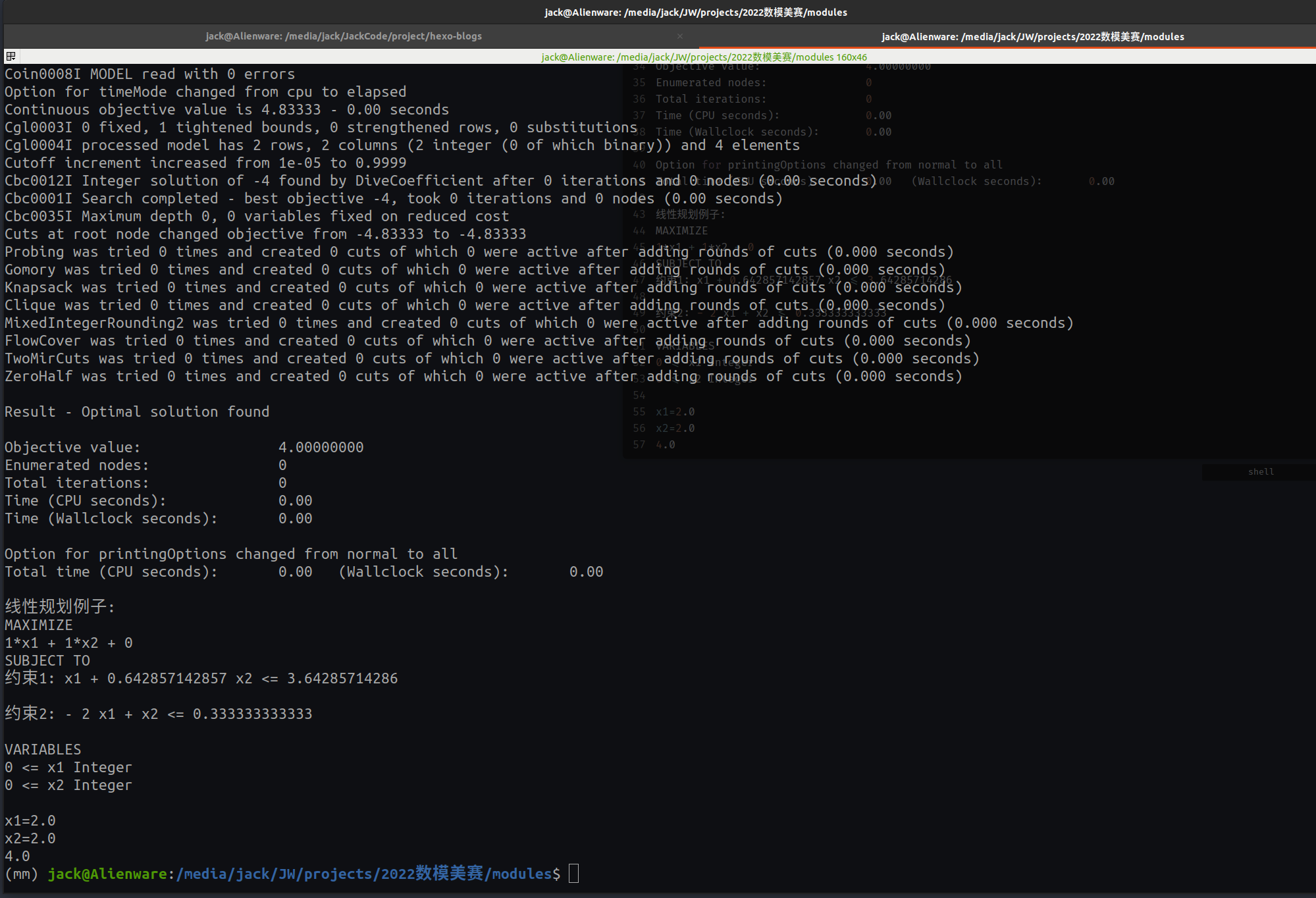
运行后的输出

Welcome to the CBC MILP Solver 
Version: 2.10.3 
Build Date: Dec 15 2019 

command line - /home/jack/anaconda3/envs/mm/lib/python3.9/site-packages/pulp/apis/../solverdir/cbc/linux/64/cbc /tmp/5cf19a184e774fe995d025bd3de8e4c9-pulp.mps max timeMode elapsed branch printingOptions all solution /tmp/5cf19a184e774fe995d025bd3de8e4c9-pulp.sol (default strategy 1)
At line 2 NAME          MODEL
At line 3 ROWS
At line 7 COLUMNS
At line 18 RHS
At line 21 BOUNDS
At line 24 ENDATA
Problem MODEL has 2 rows, 2 columns and 4 elements
Coin0008I MODEL read with 0 errors
Option for timeMode changed from cpu to elapsed
Continuous objective value is 4.83333 - 0.00 seconds
Cgl0003I 0 fixed, 1 tightened bounds, 0 strengthened rows, 0 substitutions
Cgl0004I processed model has 2 rows, 2 columns (2 integer (0 of which binary)) and 4 elements
Cutoff increment increased from 1e-05 to 0.9999
Cbc0012I Integer solution of -4 found by DiveCoefficient after 0 iterations and 0 nodes (0.00 seconds)
Cbc0001I Search completed - best objective -4, took 0 iterations and 0 nodes (0.00 seconds)
Cbc0035I Maximum depth 0, 0 variables fixed on reduced cost
Cuts at root node changed objective from -4.83333 to -4.83333
Probing was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Gomory was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Knapsack was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
Clique was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
MixedIntegerRounding2 was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
FlowCover was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
TwoMirCuts was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)
ZeroHalf was tried 0 times and created 0 cuts of which 0 were active after adding rounds of cuts (0.000 seconds)

Result - Optimal solution found

Objective value:                4.00000000
Enumerated nodes:               0
Total iterations:               0
Time (CPU seconds):             0.00
Time (Wallclock seconds):       0.00

Option for printingOptions changed from normal to all
Total time (CPU seconds):       0.00   (Wallclock seconds):       0.00

线性规划例子:
MAXIMIZE
1*x1 + 1*x2 + 0
SUBJECT TO
约束1: x1 + 0.642857142857 x2 <= 3.64285714286

约束2: - 2 x1 + x2 <= 0.333333333333

VARIABLES
0 <= x1 Integer
0 <= x2 Integer

x1=2.0
x2=2.0
4.0

8. 整数规划的例子

最后举一个真实的整数规划的数学建模的例子结束这一章

A. 最优生产问题

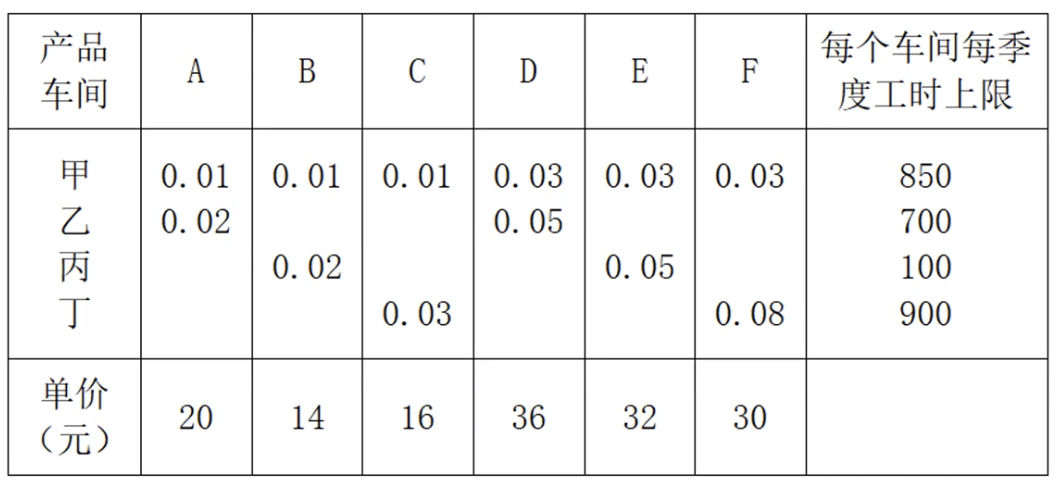
已知AM工厂是一个拥有四个车间的玩具生产厂商，该厂商今年新设计出A、B、C、D、E、F六种玩具模型，根据以前的生产情况及市场调查预测，得知生产每单位产品所需的工时、每个车间在一季度的工时上限以及产品的预测价格，如下表所示。问∶每种设计产品在这个季度各应生产多少，才能使AM工厂这个季度的生产总值达到最大?

B. 基本假设

• 利润越高越好
• 各个种类玩具都为整数

C. 符号假设

• 设各种玩具生产数量为$x_i, i=1,\cdots,6$，则$x_i$为整数
• 设利润为$Z$，则$Z=20x_1+14x_2+16x_3+36x_4+32x_5+30x_6$

D. 模型建立

根据题意，得到下面的整数规划模型

$$\max_{\vec x} z=[20,14,16,36,32,30]\vec x^T\\ \begin {cases} [0.01, 0.01,0.01,0.03,0.03,0.03]\vec x^T\leq 850\\ [0.02, 0, 0, 0.05, 0, 0]\vec x^T\leq700\\ [0, 0.02,0,0,0.05,0]\vec x^T\leq100\\ [0,0,0.03,0,0,0.08]\vec x^T\leq900\\ x_i \ge 0,&i=1,\cdots,6 \end {cases}$$

E. 编程求解

代码如下

import pulp
import numpy as np

problem: pulp.LpProblem = pulp.LpProblem(name="玩具最优生产问题", sense=pulp.LpMaximize)

variables = np.array([pulp.LpVariable(name=f"x_{i}", cat=pulp.LpInteger, lowBound=0) for i in range(6)], dtype=object)

jia = np.array([0.01, 0.01,0.01,0.03,0.03,0.03])
yi = np.array([0.02, 0, 0, 0.05, 0, 0])
bing = np.array([0, 0.02,0,0,0.05,0])
ding = np.array([0,0,0.03,0,0,0.08])
profits = np.array([20,14,16,36,32,30])

problem += jia @ variables <= 850, "甲工厂工时约束"
problem += yi @ variables <= 700, "乙工厂工时约束"
problem += bing @ variables <= 100, "丙工厂工时约束"
problem += ding @ variables <= 900, "丁工厂工时约束"

problem.setObjective(profits @ variables)

print(problem)

if pulp.LpStatus[problem.solve()] == "Optimal":
    variable: pulp.LpVariable
    for variable in problem.variables():
        print(f"{variable.name} = {variable.varValue}")
    print(pulp.value(problem.objective))

输出

玩具最优生产问题:
MAXIMIZE
20*x_0 + 14*x_1 + 16*x_2 + 36*x_3 + 32*x_4 + 30*x_5 + 0
SUBJECT TO
甲工厂工时约束: 0.01 x_0 + 0.01 x_1 + 0.01 x_2 + 0.03 x_3 + 0.03 x_4 + 0.03 x_5
 <= 850

乙工厂工时约束: 0.02 x_0 + 0.05 x_3 <= 700

丙工厂工时约束: 0.02 x_1 + 0.05 x_4 <= 100

丁工厂工时约束: 0.03 x_2 + 0.08 x_5 <= 900

VARIABLES
0 <= x_0 Integer
0 <= x_1 Integer
0 <= x_2 Integer
0 <= x_3 Integer
0 <= x_4 Integer
0 <= x_5 Integer


Result - Optimal solution found

Objective value:                1250000.00000000
Enumerated nodes:               0
Total iterations:               0
Time (CPU seconds):             0.00
Time (Wallclock seconds):       0.00

Option for printingOptions changed from normal to all
Total time (CPU seconds):       0.00   (Wallclock seconds):       0.00

x_0 = 35000.0
x_1 = 5000.0
x_2 = 30000.0
x_3 = 0.0
x_4 = 0.0
x_5 = 0.0
1250000.0